Московский технический университет по связи и информатике

Заочная форма обучения

Курсовая работа по предмету: Информатика

Тема: Численные методы и оптимизация

Студента 2 курса

Специальности 201000

Студенческий билет

№ 3МС03510

Преподаватель:

Н.Новгород

2004 год

Задание

1. Для заданной функции y(x) методом наименьших квадратов для степенного базиса получить линейную F₁(x) = a₀ + a₁x и квадратичную F₂(x) = a₀ + a₁x + a₂x² аппроксимирующие функции:

• составить и решить систему нормальных уравнений;

• определить параметры аппроксимирующих функций;

• вычислить значения аппроксимирующих функций в узлах аппроксимации;

• построить график заданной функции (множество точек) и графики функций линейной и квадратичной аппроксимации;

• оценить качество аппроксимации.

2. Найти два корня уравнения F₂(x) = 0 с заданной точностью Е:

• отделить корни;

• проверить (аналитически) условия сходимости применяемых методов решения уравнений. В случае необходимости привести уравнение к виду, обеспечивающему сходимость процесса приближения к корню;

• выбрать начальное приближение;

• записать рекуррентную формулу для уточнения корня;

• оценить погрешность.

3. Вычислит 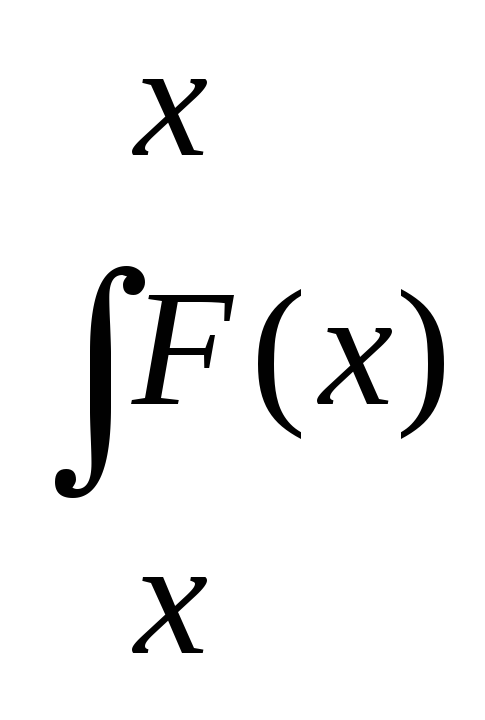dx при разбиении отрезка интегрирования на

n₁ = 10 и n₂ = 20 подынтервалов , x₁, x₂ - корни уравнения :

• оценить погрешность.

4. Определить точку экстремума функции F₂(x) методами одномерной оптимизации (с точностью Е):

• проверить условие унимодальности и выбрать начальный отрезок оптимизации;

• записать условие окончания поиска минимума (максимума) функции.

Задание 1. Функция y = y(x) задана таблицей.

Таблица 1

I	0	1	2	3	4	5
xi	0	2	4	6	8	10
y(x)	1	1.386	0.406	-0.939	-1.286	-0.266

Запишем параметры линейной аппроксимации:

x = = 4.285 y = = 0.043

a₀ = y – a₁x = 1.170952

a₁ = 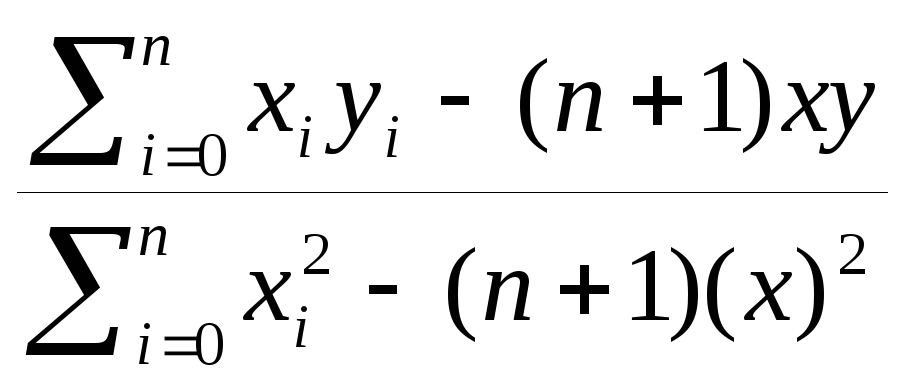= -0.2241571

Искомая линейная аппроксимирующая функция:

F₁(x) =-0.2241571х+1.170952

Составим и решим систему нормальных уравнений для определения параметров многочлена второй степени F₂(x) = a₀ + a₁x + a₂x²

(n+1)a₀ + ( Σx_i )a₁ + ( Σx_i²)a₂ = Σ y_i

( Σx_i )a₀ + ( Σx_i²)a₁ + ( Σx³)a₂ = Σ x_i y_i

(Σx_i²)a₀ + ( Σx_i³ )a₁ + ( Σx_i⁴)a₂ = Σ x_i² y_i .

Система нормальных уравнений:

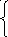6а₀ 30а₁ + 220а₂ = 0.301

30а₀ + 220а₁ - 1800а₂ = -14.186

220а₀ - 1800а₁ + 15664а₂ = -130.668

Решение системы нормальных уравнений:

а₂ = 2.545535Е-02 а₁ = -0.4787107 а₀ = 1.510357

Искомая аппроксимирующая функция:

F₂(x) = 2.545535E-02 x² – 0.4787107 x 1.510357

Значения аппроксимирующих функций F1{x} и F2{x} в узлах аппроксимации приведены в таблице 3:

X	0	2	4	6	8	10
F1{x}	1.170952	0.722638	0.274323	-0.1739	- 0.6223	-1.0706
F2{x}	1.51035	0.65475	2.799E-03	-0.4455	-0.6901	-0.7312

Таблица3

Графики функций линейной и квадратичной аппроксимации показаны на рисунке

Оценим качество аппроксимации:

ρ = sqr(1/(n+1)* ∑ (F_m(x_i) – y(x_i))²)

^{Для линейной функции: р1=0.5999658}

^{Для квадратичной функции: р2=0.5435526}

p2<p1, значит аппроксимация квадратичной функции более качкственная.

Задание 2. Решение уравнения F₂(x) с точностью Е = 10^-4 . Для отделения корней уравнения F₂(x)

составим таблицу знаков функции F₂(x).

Таблица 4

X	-1	1	3	5	7	9	11	13	15
Sign F2(x)	+	+	+	-	-	-	-	-	+

На отрезках [3 5] и [12 15] функция F₂(x) меняет знаки, т.е. существует, по крайней мере, по одному корню.

Производная F₂'(x) = 0.051x-0.4787107,

F₂"(x) = 0.051 > 0, следовательно, производная F₂'(x) - монотонно возрастающая функция.

Составим таблицу знаков функции Аэ(ч) на выбранных отрезках:

X	3	5	13	15
Sign F2’(x)	-0.32571	-0.2237	0.18423	0.2863

На отрезке [3;5] функция F₂(x) монотонно убывает, причем F₂'(x) сохраняет знак, отрезок [3;5] содержит корень.

На отрезке [13;15] функция F₂(x) монотонно возрастает, причем F₂'(x) сохраняет знак, отрезок [13;15] содержит корень.

Уточним корни методом Итераций. Воспользуемся предложенной методикой получения функции.

F2(x) – дифференцируемая и имеет разные знаки на отрезках [3;5] и [13;15].

F2’(3)<0, F2’(5)<0, F2’(x)=0

F2’(13)>0, F2’(15)>0, F2’(x)=0

Интегрирующая функция (x) = *F2(x) + x обеспечивает выполнение условий сходимости | (x)|<1

Правила выбора параметра :

-1/r < <0, если F2’(x) > 0

0 < <1/r, если F2’(x) , 0,

r = max (|F2’(a)|,|F2’(b)|).

На отрезке [3;5] r = max (0.32;0.22), следовательно, r = 0.32.

Т.к. F2’ < 0, 0 < <1/0.32, пусть = - 2/

На отрезке [13; 15] r = max (0.18;0.28), следовательно, r = 0.28

Т.к. F2’(x)>0, -1/0.28 < < 0, пусть = - 2

На отрезке [3;5] =2 x0=4

На отрезке [13;15] =-2 x0=15

Условия окончания поиска корня:

|Xn – Xn+1| < E

F2’(Xm) – F2(Xm+1) < E

Оценка погрешности корня:

|x*-xn| <= m*q/(1-q); q=max | ‘(x)|; m= |x0 - (x0)|.

На отрезке [3;5]:q=1.5963,

(x)=x; (4) = 3.98624

M=0.01376.

На отрезке [13;15]: ‘(x)=0.106349x, q=1.5952,

(14) = 13.5772; m=0.4227.

Результаты решения уравнений F2(x):

На отрезке [3;5] x = 4.0101372

На отрезке [13;15] x = 14.795575

Задание 3. Интеграл F₂(x)dx вычислить, полагая n = 10 и n = 20 методами Симпсона, трапеций и средних прямоугольников.

Формула метода средних прямоугольников:

∫ F₂(x)dx = h Σ F₂(α + kh ) ,k-степень используемого полинома, k=2

где α = а + , h = x_i+1 – x_i =

Формула метода трапеций:

∫ F₂(x)dx = (F₂(a) + F₂(b) + 2 Σ F₂ (α + ih ),

где h = x_i+1 – x_i = ,

Формула метода Симпсона:

∫ F₂(x)dx = [(F₂(a) + F₂(b) + 4 (F₂(x₁) + F₂(x₃) + … + F₂(x_2n-1)) + 2( F₂(x₂) + F₂(x₄) + … + F₂(x_2n-2)) ] ,

где h = x_i+1 – x_i = ,

Результаты занесем в таблицу .

n	Метод средних прямоугольников	Метод трапеций	Метод Симпсона
10	I = -5.349468	I = -5.269625	I = -5.322854
20	I = -5.329504	I = -5.309546	I = -5.322853

Оценка погрешности по правилу Рунге: R =|Ih-Ih/2|/(2^k-1)

Для методов средних прямоугольников и трапеций k = 2 ,

R_ср.пр. = 6.6546E-03 R_трап. = 1.3307E-02

Для метода Симпсона k = 4 , R_с = 1E-09

Задание 4. Для нахождения точки экстремума применим методы дихотомии и золотого сечения. Проверка унимодальности необходима для использования указанных методов оптимизации.

f(x) = F₂(x)

F2(x) = 2.545536E-02*x^2 – 0.474787107*x*1.510357

F’’(x) = 0.509, f’’(x) > 0, следовательно,

F2(x) – унимодальная схема и имеет локальный минимум. «Золотое сечение осуществляется двумя точками:

X1 = a+(3- 5)/2*(b – a ) = a+k1(b-a),

X2 = a+( - 1)/2*(b-a)=a+k2(b-a),

Где x1 – вторая точка золотого сечения отрезка [a;x2],

X2 – первая точка золотого сечения отрезка [x1;b].

X*=(an + bn)/2.

Взяв в качестве натурального отрезка [0 ; 2] и точность =0.0001, получим:

Xm = 1.999959, f(xm) = fm = 0.6547724