Методические указания Гриценко

2

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

СЕВЕРО-КАВКАЗСКИЙ ФИЛИАЛ

КАФЕДРА ОБЩЕНАУЧНОЙ ПОДГОТОВКИ

ГРИЦЕНКО Л.В., КОСТЕЦКАЯ Г.С.

Применение производной к исследованию функции

и построению графика.

Методические указания к индивидуальным заданиям

по разделу курса математического анализа

Ростов-на-Дону

2013

УДК 517.1 (07)

ББК 22.161

Е 91

Гриценко Л.В., Костецкая Г.С. Применение производной к исследованию функции и построению графика. Методические указания к индивидуальным заданиям по разделу курса математического анализа. Ростов-на-Дону: СКФ МТУСИ, 2013. – 59 с.

Качественное усвоение курса математики невозможно без регулярной самостоятельной работы студентов. Настоящее пособие содержит индивидуальные задания для самостоятельной работы. Приведен образец выполнения задания и 2 комплекта по 25 индивидуальных заданий. Может быть использовано для проведения практических занятий по математике, самостоятельных работ под руководством преподавателя, для проведения проверочных работ.

Печатается в соответствии с решением кафедры общенаучной подготовки СКФ МТУСИ, протокол № 1 от 2 сентября 2013 г.

Рецензент: Константинова Я.Б., кандидат физ.-мат. наук, доцент кафедры ОНП СКФ МТУСИ

Содержание

1. Справочные материалы…………………………………………………………4

2. Образец задания………………………………………………………………….8

3. Образец выполнения задания…………………………………………………...9

4. Варианты заданий……………………………………………………………...19

Комплект 1……………………………………………………………………..19

Комплект 2……………………………………………………………………..38

Литература………………………………………………………………………...59

СПРАВОЧНЫЕ МАТЕРИАЛЫ

Правила дифференцирования

1. ;

.

2. ; ; .

3. – уравнение касательной.

4. – уравнение нормали.

5. ; ; .

,

,

.

6. – сложная функция.

или .

7. – взаимообратные функции.

.

8. – параметрически заданные функции.

или ; , т.е. .

Таблица производных

1. , ;

2. ;

3. ;

4. ;

5. ;

6. , , ;

7. ;

8. , , ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. ;

20. ;

21. .

Таблица производных сложной функции

1. ;

2. ;

3. ;

4. ;

5. , , ;

6. ;

7. , , ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. .

Образец задания

1. Найти производную функции .

2. Используя логарифмическое дифференцирование, найти производную функции .

3. Составить уравнение касательной к кривой в точке с абсциссой .

4. Найти производную если функция задана параметрически:

при .

5. Найти экстремумы функции .

6. Найти частные производные функции по каждой их независимых переменных.

7. Найти производную от функции , заданной неявно.

8. Найти производную функции указанного порядка в заданной точке : , .

9. Провести полное исследование функции и начертить график.

10. Исследовать функцию на экстремум.

Образец выполнения задания

Задание 1

Найти производную функции .

Решение

Используя правила дифференцирования и таблицу производных, получим:

Ответ: .

Задание 2

Используя логарифмическое дифференцирование, найти производную функции .

Решение

Логарифмическое дифференцирование выполняется в следующей последовательности:

1. обе части уравнения логарифмируем по основанию

;

2. применяем свойство логарифма, получим ;

3. дифференцируем обе части равенства

;

4. после упрощения получим

.

Ответ: .

Задание 3

Составить уравнение касательной к кривой в точке с абсциссой .

Решение

Уравнение касательной имеет вид:

.

Найдем производную .

.

Вычислим . .

Запишем уравнение касательной:

Ответ:

Задание 4

Найти производную если функция задана параметрически:

при .

Решение

Производная находится по формуле:

Найдем

Найдем

Отсюда

Вычислим

Ответ:

Задание 5

Найти экстремумы функции .

Решение

1. Найдем область определения функции: .

2. Найдем критические точки:

.

3) Исследуем критические точки с помощью достаточных условий экстремума:

			

4) Вычислим значение функции в точках и :

Ответ:

Задание 6

Найти частные производные функции по каждой их независимых переменных.

Решение

;

.

Ответ: ,

.

Задание 7

Найти производную от функции , заданной неявно.

Решение

Для нахождения производной нужно:

1) продифференцировать обе части равенства по , учитывая, что есть функция от :

2) Из полученного уравнения находим :

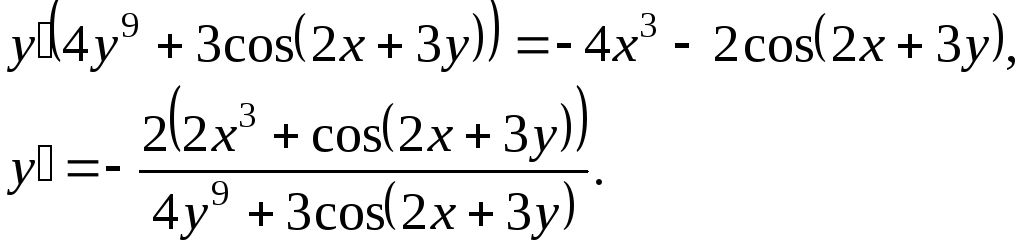
Ответ: .

Задание 8

Найти производную функции указанного порядка в заданной точке : , .

Решение

Последовательно дифференцируя , находим первую, вторую и третью производные:

Ответ:

Задание 9

Провести полное исследование функции и начертить график.

Решение

Полное исследование функции и построение графика проводится по схеме:

1. Область определения функции ;

2. точки разрыва второго рода и вертикальные асимптоты;

3. четная функция;

4. точки пересечения с осью : нет точек пересечения;

5. точки пересечения с осью : ;

6. уравнение наклонной асимптоты имеет вид :

получаем ;

7. находим интервалы возрастания, убывания и экстремумы функции, используя первую производную:

при ;

не существует при , но эти точки не принадлежат области определения

		не существует				не существует
		не существует				не существует

;

8. находим интервалы выпуклости, вогнутости, точки перегиба, используя вторую производную:

, .

не существует при , но точки не принадлежат области определения

		не существует		не существует	
		не существует		не существует

9. Построим график функции

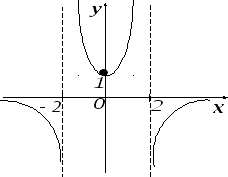
Задание 10

Исследовать функцию на экстремум.

Решение

1. Находим частные производные первого порядка

Составим и решим систему уравнений

.

Таким образом, точка критическая.

2. Находим частные производные второго порядка

.

Для точки получим .

Вычислим .

Согласно достаточному условию в точке экстремума нет.