
- •Дополнительные главы
- •Список литературы
- •Методические указания по изучению курса Анализ цепей с распределёнными параметрами.
- •1. Первичные параметры длинной линии.
- •2. Уравнения передачи однородной линии.
- •3. Падающие и отражённые волны.
- •4. Вторичные параметры.
- •5. Входное сопротивление линии.
- •5.1. Определение входного сопротивления.
- •5.2. Определение вторичных параметров.
- •5.3. Определение первичных параметров.
- •6. Линия без искажений.
- •7. Линия без потерь.
- •8. Принципы использования отрезков длинных линий.
- •8.1. Линия как фидер.
- •8.2. Применение линий для измерений.
- •8.3. Линия как элемент резонансной цепи.
- •2.3. Построение дуальных схем.
- •2.4. Аппроксимация частотных характеристик.
- •2.4.1. Аппроксимация по критерию Тейлора.
- •2.4.2. Аппроксимация по критерию Чебышёва.
- •2.5. Реализация аппроксимирующей функции электрической цепью.
- •2.6. Метод преобразования частотной переменной.
- •2.7. Активные фильтры.
3. Падающие и отражённые волны.
Для установившегося режима гармонических колебаний мгновенные напряжения и токи в любой точке линии можно представить в виде суммы падающих и отражённых волн напряжения и тока:
![]()
Отраженные волны возникают в конце линии. Комплексные значения напряжения и тока также равны сумме комплексных значений падающей и отраженной волн:
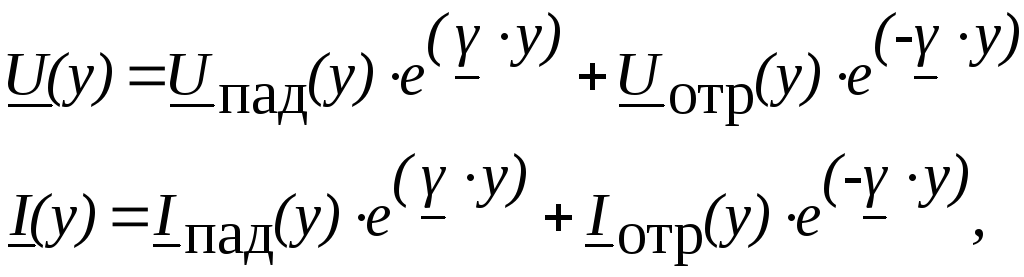
![]()
где
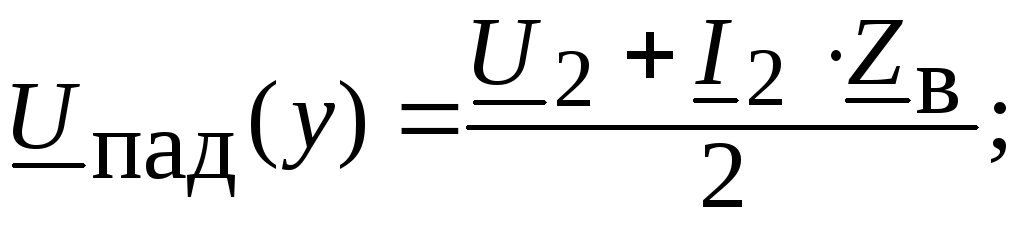
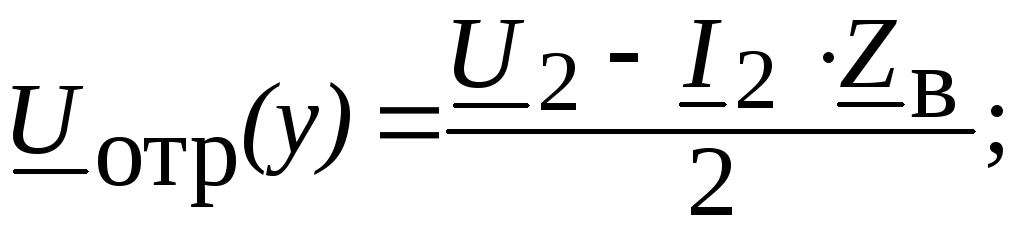
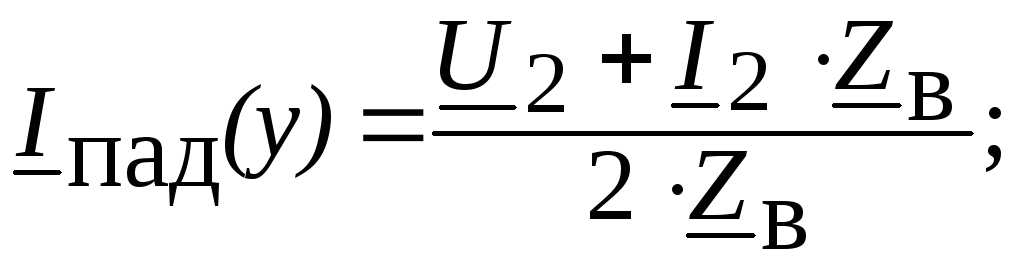
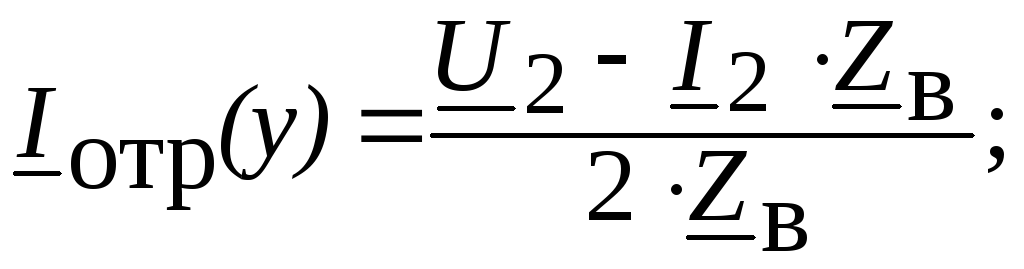
Переходя к мгновенным значениям и учитывая, что
![]()
(α - коэффициент ослабления, β - коэффициент фазы) и
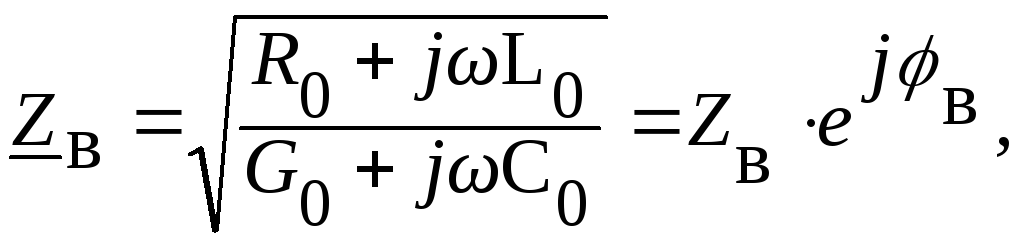
получаем:
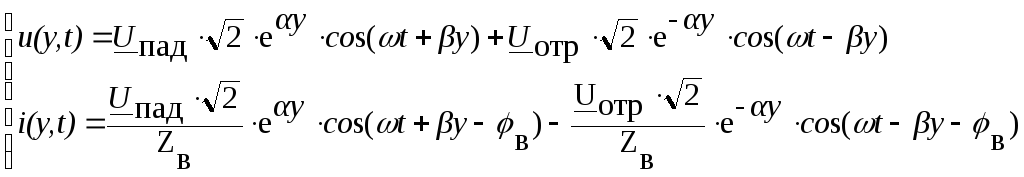 (3.1)
(3.1)
К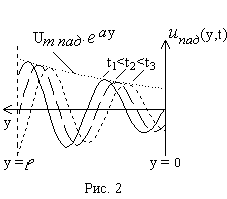 аждое
из слагаемых в правой части уравнений
(3.1) можно рассматривать как бегущую
волну, движущуюся в направлении
возрастания или убывания координатыy
и затухающую в направлении движения
(рис. 2). Основными характеристиками
бегущей волны являются фазовая
скорость и
длина волны.
аждое
из слагаемых в правой части уравнений
(3.1) можно рассматривать как бегущую
волну, движущуюся в направлении
возрастания или убывания координатыy
и затухающую в направлении движения
(рис. 2). Основными характеристиками
бегущей волны являются фазовая
скорость и
длина волны.
Фазовой
скоростью vф
волны называется скорость перемещения
фазы колебания, которая в течение времени
t
и по мере увеличения расстояния,
пройденного волной, остаётся постоянной,
то есть:
![]() откуда следует, что
откуда следует, что
![]() и
и
![]() .
.
Длиной
волны λ называется расстояние между
ближайшими двумя точками, взятое в
направлении распространения волны,
фазы колебания в которых различаются
на 2π. Следовательно, для первых слагаемых
уравнений (3.1) получается
![]() откуда
откуда
![]() и
и
![]()
Отношение
комплексной амплитуды отражённой волны
к комплексной амплитуде падающей волны
в точке y=0
(или
![]() )
называетсякоэффициентом
отражения
от выходных зажимов линии. Из выражения
(2.10 а) следует, что:
)
называетсякоэффициентом
отражения
от выходных зажимов линии. Из выражения
(2.10 а) следует, что:
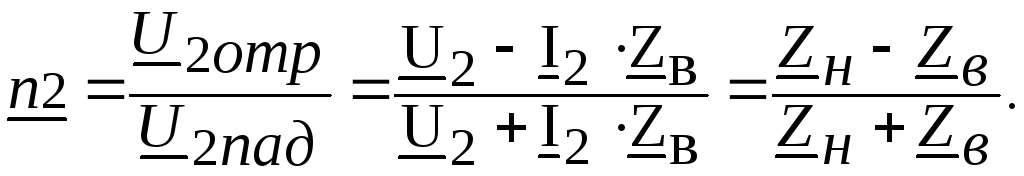
Коэффициент
отражения показывает, какую часть
амплитуды падающей волны в конце линии
составляет амплитуда отражённой волны.
Величина коэффициента отражения зависит
от режима работы линии. При согласованной
нагрузке, то есть когда
![]() коэффициент отражения
коэффициент отражения![]() ,
в этом случае отражённых волн в линии
не будет. При коротком замыкании выходных
зажимов линии (
,
в этом случае отражённых волн в линии
не будет. При коротком замыкании выходных
зажимов линии (![]() )
)![]() то есть
то есть![]() В режиме холостого хода (при разомкнутых
выходных зажимах:
В режиме холостого хода (при разомкнутых
выходных зажимах:![]() )
)![]() и
и![]() Следовательно, модуль коэффициента
отражения может меняться в пределах
Следовательно, модуль коэффициента
отражения может меняться в пределах![]()
4. Вторичные параметры.
К оэффициент
распространения (2.6) и волновое
сопротивление (2.8) называются вторичными
параметрами линии. Представим волновое
сопротивление в показательной форме:
оэффициент
распространения (2.6) и волновое
сопротивление (2.8) называются вторичными
параметрами линии. Представим волновое
сопротивление в показательной форме:
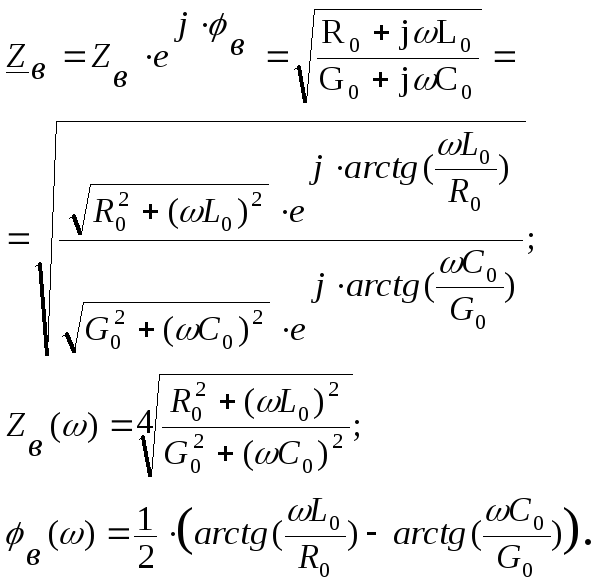
Примерные зависимости
![]() и
и![]() показаны на рисунке 3. В реальных линиях
обычно
показаны на рисунке 3. В реальных линиях
обычно![]() ,
поэтому модуль волнового сопротивления
с частотой уменьшается.
,
поэтому модуль волнового сопротивления
с частотой уменьшается.
Для
линии с малыми потерями коэффициент
распространения
![]() можно представить следующим образом:
можно представить следующим образом:
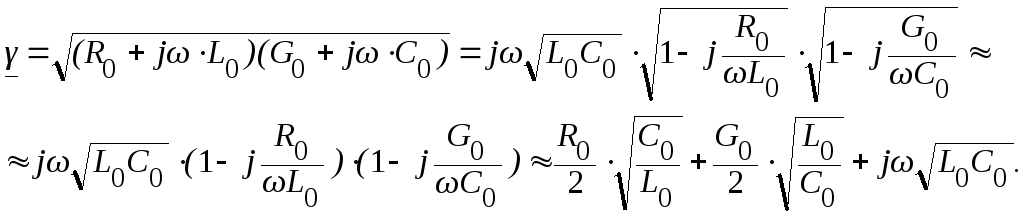
Отсюда следует, что
![]() ,
,
![]() ,
,
![]() .
.
5. Входное сопротивление линии.
![]() и
и
![]() - комплексные значения напряжения и
тока на расстоянии «у»
от конца линии.
- комплексные значения напряжения и
тока на расстоянии «у»
от конца линии.
Входное
сопротивление линии в точке с координатой
«y»
определяется отношением напряжения
![]() и тока
и тока![]() .
Выражение для
.
Выражение для![]() учитывая (2.10 б), записывается в виде
учитывая (2.10 б), записывается в виде
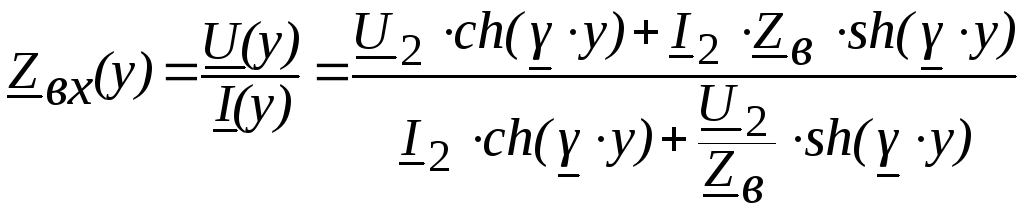 ,
или, с учётом
,
или, с учётом
![]() ,
,
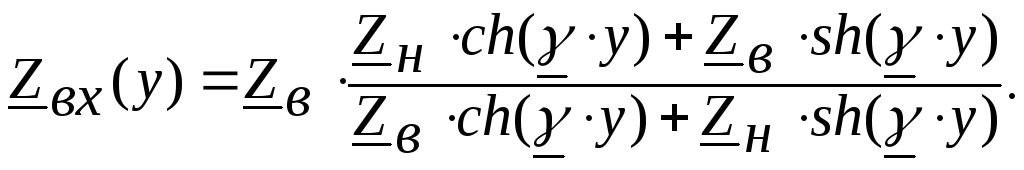 (5.1)
(5.1)
При
согласованном включении линии (![]() )
из (5.1) получим, что
)
из (5.1) получим, что![]() .
.
Если
выходные зажимы линии замкнуты накоротко
(![]() ):
):
![]() (5.2)
(5.2)
В
случае разомкнутых выходных зажимов
(режим холостого хода
![]() ):
):
![]() (5.3)
(5.3)
5.1. Определение входного сопротивления.
Можно
рассчитать входное сопротивление линии
в точке с координатой «y» по измеренным
значениям сопротивлений холостого хода
и короткого замыкания. Разделив числитель
и знаменатель (5.1) на
![]() получим:
получим:
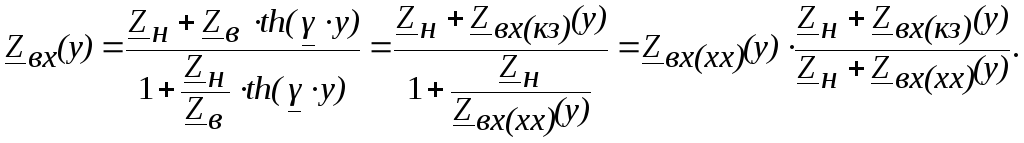 (5.4)
(5.4)
