
- •2.Затухающие колебания
- •2.1 Общие представления и понятия
- •2.2 Элементы теории.
- •2.3 Задачи
- •3 Вынужденные колебания
- •3.1 Общие представления
- •3.2 Элементы теории
- •1Нт1(з) На рисунке приведена векторная диаграмма вынужденных колебаний в электрическом контуре
- •3.3 Задачи
- •Раздел 1. Общие представления о волнах.
- •1.1 Основные определения и понятия.
- •1.2.Элементы теоретического описания
- •1.3 Задачи
- •Раздел 2. Электромагнитные и упругие волны.
- •2.1. Основные определения и понятия.
- •2.2. Элементы теоретического описания.
- •2.3. Задачи.
- •Раздел 3. Сложение волн и интерференция.
- •3.1. Основные определения и понятия
- •3.2 . Элементы теоретического описания.
- •3.3. Задачи
- •Л 4. Элементы волновой оптики (дифракция света).
- •4.1. Основные определения и понятия.
- •4.2. Элементы теоретического описания.
- •14. (Нт1). (з). Интенсивность на экране в центре дифракционной картины от диафрагмы, на которой укладываются 3 зоны Френеля, равна l1, а при отсутствии диафрагмы равна l0. При этом:
- •15. (Нт2). (з). Амплитуда волны в точке наблюдения, если на ее пути установить экран, открывающий 3,5 зоны Френеля,
- •31. (Нt1). (з). Угловые дисперсии спектров 2-го порядка (d2) и 4--го порядка (d4) связаны отношением:
- •35. (Нt1). (з). Если увеличить период дифракционной решётки в 2 раза, то угловая дисперсия в спектре 2-го порядка:
- •36. (Нt1). (з). Плоская монохроматическая световая волна нормально падает на узкую щель. При увеличении ширины щели в два раза угловая ширина центрального максимума:
- •38. (Нt2).(з). На рис. Приведены спектры одного порядка для 2-х дифракционных решёток (d- период, n – число штрихов на всей решётке).
- •39. (Нт2). (з). Максимальный порядок спектра дифракционной решетки с периодом d при освещении светом с длиной волны λ определяется соотношением
- •40.(Нт1). (з). Положение главных максимумов после прохождения дифракционной решетки светом с длиной волны определяется параметром (см. Рисунок) :
- •4.3. Задачи.
3.2 Элементы теории
1Нт1(з) На рисунке приведена векторная диаграмма вынужденных колебаний в электрическом контуре

А)
рост заряда на конденсаторе опережает,
а тока отстает по фазе от роста внешнего
напряжения
![]()
В)
q(t)
- отстает, а![]() опережает по фазе изменение
опережает по фазе изменение
![]()
С)
q(t)
отстает по фазе на
![]() а ток на
а ток на
![]() +
+
![]() изменение
изменение
![]()
*D)
![]() отстает
по фазе на
отстает
по фазе на
![]() ,
а ток опережает на –
,
а ток опережает на –
![]() рост
рост
![]()
2НТ1(З)
Сдвиги фаз изменения
![]() ,
тока I
= и заряда q
при вынужденных
колебаниях равны:
,
тока I
= и заряда q
при вынужденных
колебаниях равны:
А) и I равен всегда π , и q -
*В) и q равен всегда π; – относительно на +
C)
и q
меняется от
0 до π при изменении ω от 0 до ∞ ![]() - всегда сдвинута на
- всегда сдвинута на
![]() относительноq
относительноq
D)
и q
равен всегда
π, q
относительно
![]() = I
на + (опережает) при ω < ω0
и на - (запаздывает) при ω
> ω0
= I
на + (опережает) при ω < ω0
и на - (запаздывает) при ω
> ω0
3НТ2(З)
Сдвиг фаз изменения ЭДС самоиндукции
![]() ,напряжения
на резисторе (UR)
и напряжения на конденсаторе
,напряжения
на резисторе (UR)
и напряжения на конденсаторе ![]() при вынужденных
гармонических колебаниях в электрическом
контуре :
при вынужденных
гармонических колебаниях в электрическом
контуре :
*А)
![]() относительно
UC
всегда «0»,
UR
относительно
относительно
UC
всегда «0»,
UR
относительно
![]() :
+
:
+
В)
![]() относительно UC
всегда π, UR
относительно
относительно UC
всегда π, UR
относительно
![]() :
+
:
+
С)
![]() относительно
UC:
+π, ω < ω0
; -π, ω > ω0
UR
относительно
относительно
UC:
+π, ω < ω0
; -π, ω > ω0
UR
относительно ![]() :
+
:
+
D)
![]() по отношению к
UC
всегда 0 UR
по отношению к UC
+ ω < ω0,
- ω >ω0
по отношению к
UC
всегда 0 UR
по отношению к UC
+ ω < ω0,
- ω >ω0
4НТ1(О) На рисунке представлена векторная диаграмма резонанса амплитуды заряда вынужденных гармонических колебаний в электрическом контуре. Частота вынужденных колебаний ……собственной частоты контура.

Ответ: меньше
5НТ1(З)
На рисунке приведена зависимость сдвига
фазы смещения механических колебаний
пружинно маятника от
![]() при
разных β
относительно фазы вынуждающей
гармонической силы
при
разных β
относительно фазы вынуждающей
гармонической силы

*А) β1 < β2 < β3
B) β1 > β2 > β3
C)
Приведенные кривые не отражают реальной
ситуации, т.к.
Ψ
(![]() )
не зависит от β
)
не зависит от β
D)
По приведенным кривым установить
соотношение между βi
нельзя т.к. Ψ
(![]() )
также функция амплитуды колебаний
)
также функция амплитуды колебаний
6НТ1(З) При резонансе сдвиг фазы между вынуждающей силой и смещением в механических колебаниях равен
А)
![]()
В)
*С)
![]()
D)
![]()
7НТ1(З) В электрическом контуре при резонансе тока сдвиг фазы между внешней ЭДС (ε(t)) и зарядом (q(t)) конденсатора равен :
А) 0
В)
С) - π
*D)
![]()
8НТ1(З) В электрическом контуре при резонансе тока сдвиг фазы между внешней ЭДС (ε(t)) и током равен:
*А) 0
В)
С)
D) π
9НТ1(З) Амплитуда тока при резонансе тока в электрическом контуре равна
*А)
В)
![]()
C)
![]() ,
где Q
- добротность контура
,
где Q
- добротность контура
D)
![]()
10НТ1(З) При резонансе электрического заряда ( напряжения UC) сдвиг фазы между током (напряжением UR) и ЭДС источника вынуждающих колебаний
*А) ,( << 1)
В)
+![]() (
(![]() <<
1)
<<
1)
C)
![]()
D)
![]()
11НТ2(З) Векторная диаграмма построена для механических вынужденных колебаний при следующих соотношениях между ω0, ω и β, (ω0 - собственная частота колебаний: ω - частота вынужденных колебаний, β- коэффициент затухания )

A.
![]()
B.![]()
C.![]()
D.![]()
12НТЗ(З) На векторной диаграмме, построенной для механических вынужденных колебаний сдвиг фаз между вынуждающей силой и смещением равен:
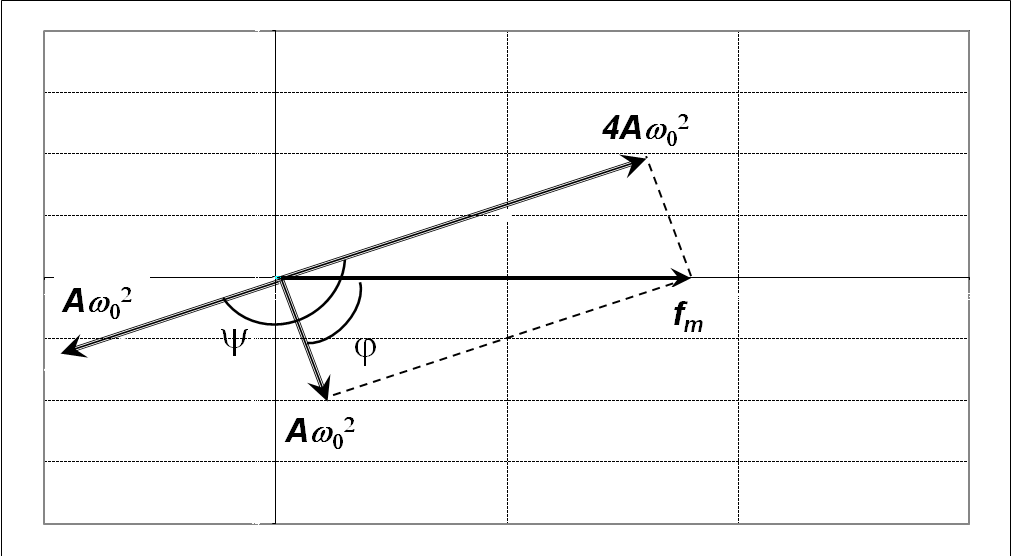
А.≈ 72°
* В. ≈162°
C. ≈ 29°
D. ≈ 90°
13НТ2(З) При вынужденных колебаниях в электрическом контуре выполняется условие
A.![]() всегда
всегда
B.![]() всегда
всегда
C.![]() всегда
всегда
*D.
может быть как![]() ,
так и
,
так и![]()
(![]() -
максимальное значение амплитуды
напряжения на конденсаторе,Emax-
амплитуда внешней ЭДС)
-
максимальное значение амплитуды
напряжения на конденсаторе,Emax-
амплитуда внешней ЭДС)
14НТ2(З) При вынужденных колебаниях в электрическом контуре выполняется условие
A.![]() всегда
всегда
*B.![]() всегда
всегда
C.![]() всегда
всегда
D.
может быть как![]() ,
так и
,
так и![]()
(![]() -
максимальное значение амплитуды
напряжения на сопротивлении,Emax-
амплитуда внешней ЭДС)
-
максимальное значение амплитуды
напряжения на сопротивлении,Emax-
амплитуда внешней ЭДС)
15НТ2(З) При вынужденных колебаниях в электрическом контуре выполняется условие
A.![]() всегда
всегда
B.![]() всегда
всегда
C.![]() всегда
всегда
*D.
может быть как![]() ,
так и
,
так и![]()
(![]() -
максимальное значение амплитуды
напряжения на катушке индуктивности,Emax-
амплитуда внешней ЭДС)
-
максимальное значение амплитуды
напряжения на катушке индуктивности,Emax-
амплитуда внешней ЭДС)
16НТ2(З) Привести в соответствие номера векторов (1, 2, 3, 4) и величины, обозначенные указанными векторами (упругость - а, трение - б, инертность - в ,внешнее воздействие - г ) на векторной диаграмме, построенной для механических вынужденных колебаний.

А. 16; 2в; За; 4г.
*В. 1а; 2г; 36; 4в.
C. 1в; 26; Зг; 4а.
D. 1г; 2а; Зв; 46.
17НТ1(З) На векторной диаграмме, построенной для механических вынужденных колебаний, упругость характеризуется вектором

*А. 1
B. 2.
C. 3.
D. 4.
18НТ1(З) На векторной диаграмме, построенной для механических вынужденных колебаний, инертность характеризуется вектором

A. 1
B. 2.
C. 3.
*D. 4.
19НТ1(З) На векторной диаграмме, построенной для механических вынужденных колебаний, внешнее воздействие характеризуется вектором

А. 1
*В. 2
C. 3.
D. 4.
20НТ1(З) На векторной диаграмме, построенной для механических вынужденных колебаний, трение характеризуется вектором
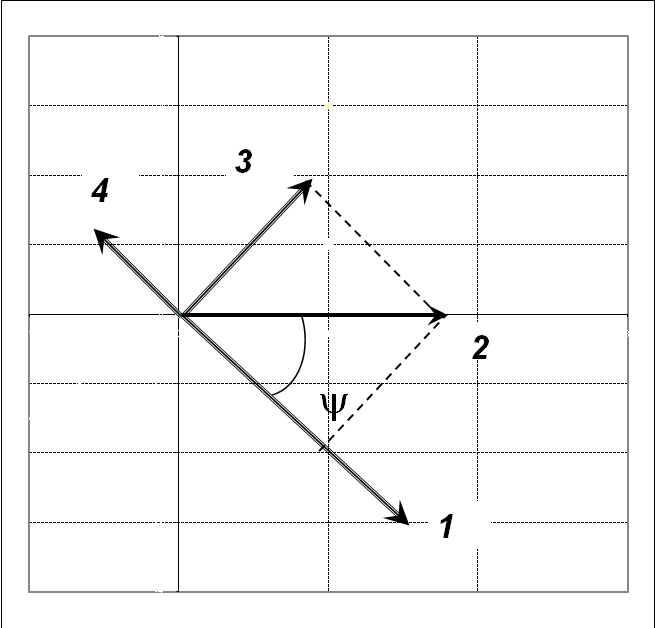
A. 1.
B. 2.
*С 3.
D. 4.
21НТ1(З) При резонансе тока в случае вынужденных колебаний в RLC контуре напряжение на резисторе (R) равно
A)
![]()
*B)
![]()
C)
![]()
![]()
D)
![]()
![]() (или
(или![]() ,
т.к.
,
т.к.
![]() =
=
![]() ),
здесь Q
- добротность контура,
),
здесь Q
- добротность контура,
![]() - амплитуда
напряжения источника вынужденных
колебаний.
- амплитуда
напряжения источника вынужденных
колебаний.
22НТ1(З) Выберите все неверные ответы
При вынужденных колебаниях в RLCконтуре сдвиг фазы между напряжениямиULиUC :
A)
Всегда равен![]()
B)
Равен![]() только при резонансе напряжения
только при резонансе напряжения![]()
C)
Равен![]() при любом резонансе
при любом резонансе![]() до резонансов и
до резонансов и![]() после
после
D) Всегда равен нулю, но при резонансеUL = UC
Ответ: B,C,D
23НТ1(З)
Известно, что при резонансе тока в RLCконтуре напряжение наRравно![]() – амплитуде напряжения источника
вынужденных колебаний. Это связано с
тем, что
– амплитуде напряжения источника
вынужденных колебаний. Это связано с
тем, что
A) Ток течёт только через резистор, а черезCне течёт
B)UL
и UC
сдвинуты по фазе относительно![]() на
на![]()
*C)UL
и UC
имеют сдвиг фазы![]() ,
а их амплитуды при
,
а их амплитуды при![]() равны
равны
D) Среднее значениеUL и UC за период равно 0
ИСПРАВИТЬ ГРАФИКИ!!!!!
24НТ1(О) На Рис.22 приведены резонансные кривые (в относительных единицах) для некоторого энергетического контура
Резонанс напряжения на резисторе описывается кривой
Ответ: 2
25НТ1(О) На Рис. (из 22) приведены резонансные кривые (в относительных единицах) для некоторого энергетического контура. Резонансная зависимость электрического заряда от частоты, описывается графиком
ГРАФИКИ!!!!!
Ответ: 1
26НТ1(З)
Если при вынужденных колебаниях сдвиг
фазы между напряжением на конденсаторе
в электрическом контуре и внешней ЭДС
равен –
![]() ,
то сдвиг фазы
,
то сдвиг фазы![]() тока относительно фазы ЭДС равен:
тока относительно фазы ЭДС равен:
A)![]()
*B)![]()
C)![]()
D)![]()
27НТ1(З)
Известно, что при вынужденных колебаниях
в последовательном RLCконтуре сдвиг фазы между внешней ЭДС и
напряжением на конденсаторе всегда <0,
а его значение определяется соотношениемtg![]() =
=![]() сдвиг фазы между током и внешней ЭДС
сдвиг фазы между током и внешней ЭДС![]() можно найти по формуле:
можно найти по формуле:
A)
B)
*C)
D)
28НТ1(З) Что бы вычислить мощность источника внешней силы ЭДС при вынужденных колебаниях в RLCконтуре необходимо определить в каждый момент:
*А)
произведению
![]()
В)
![]()
С)
![]()
D)![]()
29НТ1(З)
Мощность
![]() внешний
ЭДС при вынужденных колебаниях в
внешний
ЭДС при вынужденных колебаниях в![]() контуре
в каждый момент времени:
контуре
в каждый момент времени:
A) только ≥ 0
B)P≥ 0 при резонансах и до
резонанса; P < 0; для![]() >
>![]() (после
резонанса)
(после
резонанса)
*C)
при резонансе![]() P≥ 0; при
P≥ 0; при![]() или
или![]() имеются временные интервалы, гдеP(t) <0
имеются временные интервалы, гдеP(t) <0
D)
при всех частотах![]() имеются
в течении периода промежутки
имеются
в течении периода промежутки![]() ,
гдеp< 0, но <P>
за период всегда > 0
,
гдеp< 0, но <P>
за период всегда > 0
30НТ1(З) Средняя мощность «N», поступающая за период в контур для разных частот при вынужденных колебаниях равно:
А)
![]() ,
где
,
где![]() ,
,![]() -
сдвиг фазы между током и
-
сдвиг фазы между током и![]()
B)![]() ,
где
,
где
![]() -сдвиг
фазы межу током и
-сдвиг
фазы межу током и![]()
С)
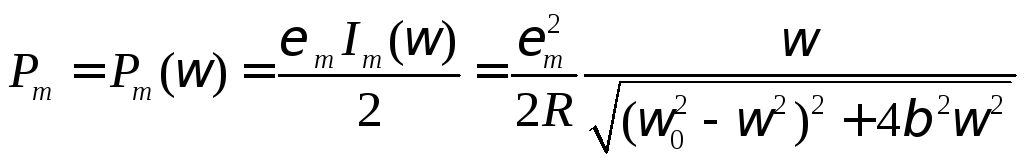
*D)![]() ,
где
,
где ,
,![]() -
сдвиг фазы между током и
-
сдвиг фазы между током и![]() (ЭДС)
(ЭДС)
31НТ1(З) В электрической цепи сдвиг фазы между током и приложенным напряжением может быть
А) только > = 0
*В) >, < и = 0
С) только > или = 0
Д) всегда < 0, так как ускорение зарядов всегда опережает скорость
32НТ1(О)
На рисунке приведены осциллограммы ЭДС
![]() источника вынужденных колебанийRLCконтура, тока в нем, и мощности токаN(t)
источника вынужденных колебанийRLCконтура, тока в нем, и мощности токаN(t)
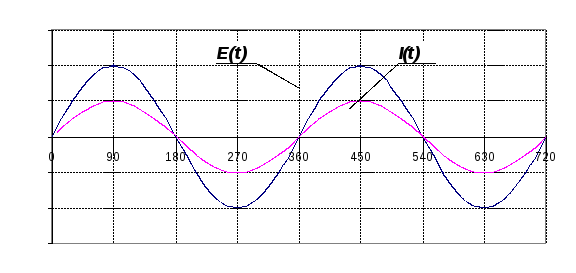

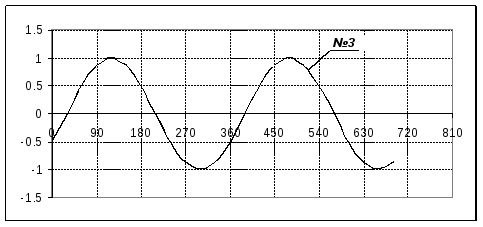



Графику для ε(t) иI(t) – 1 соответствует осциллограммаN(t)…
Ответ: 4
33НТ1(О) На рисунках приведены осциллограммы ЭДС (E(t)) источника вынужденных колебанийRLCконтура, тока нем, и мощности тока (N(t))






Графику 1 для ε(t) и 2I(t) соответствует осциллограммаN(t)…
Ответ: 6
34НТ1(З)
На рисунках Приведены осциллограммы
ЭДС
![]() (t)
источника вынужденных колебанийRLCконтура, тока нем, и мощности токаN(t)
(t)
источника вынужденных колебанийRLCконтура, тока нем, и мощности токаN(t)





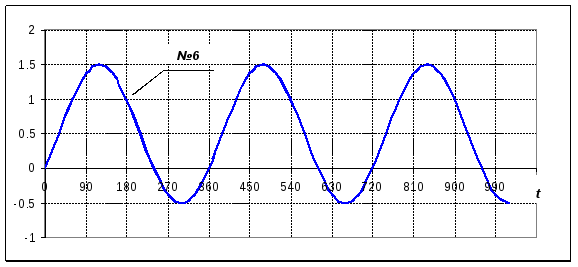
Графику 1 для ε(t) и 3I(t) соответствует осциллограммаN(t)…
Ответ: 5
35НТ1(З) На рис. приведена осциллограмма мощности тока при вынужденных колебаниях в электрическом контуре.

Энергия
за промежутки типа
![]()
А) рассеивается на активном сопротивлении контура R
В) поступает из контура в источник (ЭДС)
С) Частично рассеивается на R, частично поступает, частично увеличивает запас энергии в контуре
D) Частично рассеивается наR, частично поступает в источник
36НТ1(З) На рис. приведена осциллограмма мощности тока при вынужденных колебаниях в электрическом контуре.

Энергия за промежутки типа t3 – t2
А) рассеивается на R, частично поступает, частично увеличивает запас энергии в контуре
В) затрачивается за период источником на поддержание квазистационарной амплитуды колебаний в осцилляторе (на компенсацию потерь в R)
*С)
Энергия, поступающая в контур от источника
за период такая, что
![]() -
компенсирует Джоулевы потери наRв контуре.
-
компенсирует Джоулевы потери наRв контуре.
D)
Энергия запасенная в конденсаторе,
тогда как заt2–t1– энергия запасенная в катушке![]()
37НТ1(З) В цепях электрического тока коэффициентом мощности называют
А)
![]() - отношение мощности выделяемой в контуре
к мощности «развиваемой» источником
- отношение мощности выделяемой в контуре
к мощности «развиваемой» источником
*В)
![]() - максимальная мощность, которая может
быть передана в нагрузку на переменном
токе
- максимальная мощность, которая может
быть передана в нагрузку на переменном
токе
*С)
![]() - где
- где![]() -
сдвиг фазы между током и напряжением
на нагрузке
-
сдвиг фазы между током и напряжением
на нагрузке
D)![]() -
где
-
где![]() -
сдвиг фазы между током и напряжением
на нагрузке
-
сдвиг фазы между током и напряжением
на нагрузке
38НТ1(З)
Если
![]() - сдвиг фазы между током и напряжением
в цепи переменного тока, то значение
- сдвиг фазы между током и напряжением
в цепи переменного тока, то значение![]() при котором будет передана в нагрузку
максимальная мощность равна:
при котором будет передана в нагрузку
максимальная мощность равна:
А)
![]()
В)
![]()
С)
![]()
*D) 0
39НТ1(З)
Если в электрическом контуре максимальное
значение электрического заряда под
действием вынуждающей силы равно
![]() .То
энергия, запасенная в случае вынужденных
колебаний при резонансе равна:
.То
энергия, запасенная в случае вынужденных
колебаний при резонансе равна:
А)
![]()
В)
![]()
С)

D)![]()
40НТ1(З)
Выберите все неверные ответы. На рисунке
приведена электрическая цепь, подключенная
к источнику с
![]() .
Максимальное значение напряжения (UL)
на индуктивности равно:
.
Максимальное значение напряжения (UL)
на индуктивности равно:

А)
![]()
В)
![]()
С)

*D)
41НТ1(З)
Выберите все неверные ответы. На рисунке
приведена электрическая цепь, подключенная
к источнику
![]() максимальное значение напряжения на
конденсаторе равно:
максимальное значение напряжения на
конденсаторе равно:
* А)
А)![]()
*В)
![]()
С)
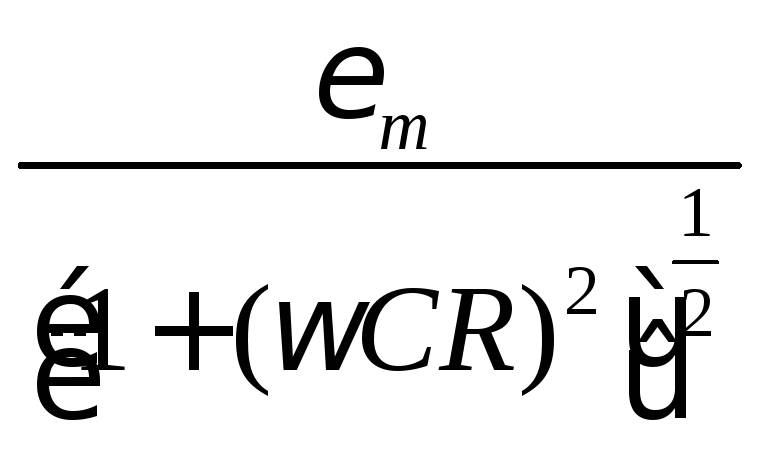
*D)
Неверные ответы: А, В, D
4 2НТ1(З)В электрической цепи, изображенной на
рисунке (последовательныйRLCконтур) реактивное сопротивлениеXравно:
2НТ1(З)В электрической цепи, изображенной на
рисунке (последовательныйRLCконтур) реактивное сопротивлениеXравно:
*А)
![]()
В)
![]()
С)
![]()
D)![]()
43НТ1(З)В электрической цепи изображенной на рисунке ( последовательныйRLCконтур ) импеданс цепиZравен:
*А)
![]()
В)
![]()
С)
![]()
D)![]()
44НТ1(З)электрической цепи изображенной на
рисунке ( последовательныйRLCконтур ) модуль полного ( комплексного)
сопротивления цепи![]() равен:
равен:
А)
![]()
В)
![]()
С)
![]()
D)![]()
45НТ1(З) Цепи изображенной на рисунке ( последовательныйRLCконтур ) напряжение(UR ,UX) и ток (IR,IX) на резисторе и реактивном сопротивлении среды по фазе:
А )
)![]() и
и![]() совпадают, токи сдвинуты на
совпадают, токи сдвинуты на![]()
*В)
токи
![]() (+) =
(+) =![]() (+) напряжение сдвинуто по фазе на
(+) напряжение сдвинуто по фазе на![]()
C)
токи![]() (+) =
(+) =![]() (+) напряжение сдвинуто по фазе на π
(+) напряжение сдвинуто по фазе на π
D)![]() =
=![]() (+)
фазы
(+)
фазы![]() иR
иR![]() совпадают
(одновременно достигают максимум и
минимум)
совпадают
(одновременно достигают максимум и
минимум)
46НТ1(З)На рис. приведена осциллограмма мощности тока при вынужденных колебаниях в электрическом контуре.

Энергия за промежутки типа t3–t2
А) частично рассеивается на R, частично поступает, частично увеличивает запас энергии в контуре
В) поступает из источника
С)
энергия, поступающая в контур от источника
за период такая, что
![]() -
компенсирует Джоулевы потери наRв контуре
-
компенсирует Джоулевы потери наRв контуре
D) Частично рассеивается наR, частично поступает в источник .
4 7НТ1(З)В электрической цепи изображенной на
рисунке при
7НТ1(З)В электрической цепи изображенной на
рисунке при![]() мощность выделяющейся в цепи равна
мощность выделяющейся в цепи равна![]() .
Если
.
Если![]() ,
то <P> равна:
,
то <P> равна:
А)
всегда
![]()
В)
![]() ,
если реактивное сопротивление равно 0
,
если реактивное сопротивление равно 0
С)
всегда

*D)
всегда меньше![]() и уменьшается с россом частоты
и уменьшается с россом частоты
4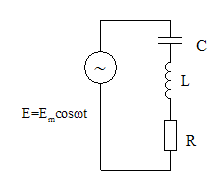 8НТ1(З)Если
8НТ1(З)Если![]() энергия запасаемая в конденсаторе
последовательного электрического
контура ( рис ) при
энергия запасаемая в конденсаторе
последовательного электрического
контура ( рис ) при![]() .
То энергия, теряемая в контуре за период
при резонансе (
.
То энергия, теряемая в контуре за период
при резонансе (![]() )
равна
)
равна
А)
![]()
В)
![]()
С)
![]()
D)![]()
Выберите все неверные ответы
Ответ: В, D
49НТ1(З)Средняя мощность выделяющаяся в электрической цепи изображенной на рисунке (последовательный контур) равна:
А)
![]() где
где![]()
В )
)![]()
С)
![]()
D)
![]()
