2.2. Элементы теоретического описания.

1. (НТ1). (З). Если ρ- удельное сопротивление среды,ε- относительная диэлектрическая проницаемость,χ- магнитная восприимчивость, то материальные уравнения для изотропной среды, входящие в систему уравнений Максвелла, имеют вид:

А); В); *С);D).

2. (НТ2). (З). Если поле , тоимеет компоненты:

A) ; *B);

C);D)

3.(HТ2). (З). Если поле, тоимеет компоненты:

A);B);

*C);D)т.к..

4.(HТ2). (З). В электромагнитной волнекомпонентыравны:

A);B); *C); *D). Неправильные соотношения:C;D

5. (HТ2). (З). В электромагнитной волнекомпонентыравны:

A)*B)C)D) В приведённых выше ответах нет правильного.

6. (HТ2). (З). В электромагнитной волне в вакуумекомпоненты роторав системе СИ равны:

A);

*B)

C)всегда равен нулю, т.к.- вихревое поле (компоненты ротора в каждый момент компенсируют друг друга) Не равна нулю дивергенцият.к.определяет плотность тока смещения т.е.источник поля;D).

7. (НТ1). (С). Выражениям в левом столбце соответствуют следующие выражения, стоящие а правом столбце:

A)B)C)D)

A) B) C) D)

Ответ: А-В, В-D, С-С,D-A.

8. (НТ1). (З). Если решение уравнения известно, то с помощью уравнения:

A) Можно найти производную, а затем и; *B) невозможно найти;C) можно найти, но лишь в отдельных случаях (при известных начальных условиях)D)определяется только потенциальная часть, т.к. решение первого уравнения даёт потенциальную составляющую поля

9. (НТ1). (З). В некоторой области пространства для электромагнитного поля оказалось: . Соотношения означают, что в этой области:

A)и- вихревые поля; *B)- вихревое (всегда!),- может быть вихревым или потенциальным;C)- вихревое поле,- потенциальное, но в рассматриваемой области нет источников;D) Для однозначного ответа недостаточно данных, т.к. неизвестно распределение токов и зарядов, а также их зависимость от времени.

10. (НТ1). (З). Если интеграл по некоторому контуру (L), то:

A) Магнитное поле отсутствует – оно всегда вихревое и порождается токами, электрическое поле – потенциальное.B) Магнитное и электрическое поля потенциальны.C) Магнитное и электрическое поля не зависят от времени и могут быть либо потенциальными либо вихревыми. *D) Электрическое поле потенциально, для магнитного поля алгебраическая сумма токов, пересекающих поверхность, охватываемую контуром, равна нулю.

11. (НТ2). (З). Постоянному полю в вакууме соответствует система уравнений Максвелла:

A);

*B);

C);

D);

12. (НТ2). (З). Переменному полю в вакууме соответствует система уравнений Максвелла:

A);

B);

C);

*D).

13. (НТ2). (З). Переменному полю в среде в общем случае соответствует система уравнений Максвелла:

A);

B);

*C);

D).

14. (НТ2). (З). Постоянному полю в среде соответствует система уравнений Максвелла:

*A);

B);

C);

D).

15. (НТ2). (З). Волновое уравнение, решением которого является плоская поперечная электромагнитная волна, можно получить из системы уравнений Максвелла:

A);

B);

C);

*D) .

16. (НТ2). (З). Плоские электромагнитные волны не являются частным решением следующих уравнений:

А) ;

B);

*C);

*D).

17. (НТ1). (З). Плоские электромагнитные волны не являются решением уравнений:

A) только при условии;

В) всегда, если ;

*C) в любой однородной изотропной линейной среде при выполнении условия:;

*D) в любой однородной изотропной линейной среде при выполнении условия:.

18. (НТ2). (З). Для плоской электромагнитной волны волновое уравнение может быть записано в виде:

А) ;

B);

*C);

D);

Неправильными выражениями являются:

19. (НТ2). (С). Установите все соответствия между правым и левым столбцам, чтобы получить волновые уравнения, частным решением которых является плоская электромагнитная волна :

A)A)

B)B)

C)C)

D)D)

Ответы: ВА; СА; АС; DC.

21. (НТ1). (З). Неверными являются соотношения :

А) ;

*B);

C);

*D).

22. (НТ1). (З). В электромагнитной волне, распространяющейся в однородном изотропном пространстве соотношение между амплитудами электрического и магнитного () полей равно:

*А) ; В); С);D).

23. (НТ1). (З). Если в плоской электромагнитной волне известно значение амплитуды электрического поля , то значение амплитуды магнитного поля () может быть определено по формуле:

*A);B);C);D).

24. (НТ1). (З). Если в плоской электромагнитной волне известно значение амплитуды электрического поля , то значение амплитуды магнитного поля () может быть определено по формуле:

A);*B);C);D).

25. ( НT1). (З).Неправильнымутверждением является:

A) электромагнитные волны в вакууме поперечные;B); *C) векторыиколеблются с фазовым сдвигом;D).

26. (НТ2). (С). Для 2-х сред с диэлектрическими проницаемостями отношению величин из левого столбика соответствуют следующие их численные значения из правого столбика:a) a) 1/2

b) b) 2

c) c) 4

d) d) 1

A) a-b, b-d, c-d, d-b; B) a-a, b-a, c-b, d-c; *C) a-b, b-d, c-b, d-c; D) a-a, b-d, c-b, d-b;

2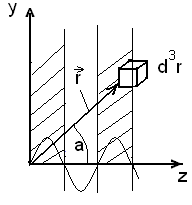7. (НТ1). (З). В заданном элементе пространства (рис.) значение вектора Пойнтинга в плоской гармонической волне :

*А) изменяется со временем по гармоническому закону с удвоенной частотой: ;

B) не зависит от времени и;

C) колеблется со временем так же как и векторы,т.е.;

D) равно.

28. (НТ2). (З). Определите все неверные ответы. ЕслиI– интенсивность волны,,- напряженности полей, - нормаль, параллельная вектору Пойнтинга (), то мощность потока энергии (Р) равна:

A)B)

C)D)

Ответы: В, D.

29. (НТ1). (З). Пусть w- плотность энергии электромагнитного поля,- вектор Пойнтинга. Модуль импульса, который переносится единицей объема волнового поля, равен :

A)(m- релятивистская масса единицы объёма поля); *B);C);D).

30. (НT2). (З). Среднее значение вектора Пойнтинга плоской электромагнитной волны в вакууме равно. Напряженность магнитного поля равна:

A); *B);C);D).

31. (НТ2). (З). Для электромагнитной волны в вакууме утверждению в левом столбике соответствует следующее соотношение, стоящее в правом столбике:

a) модуль импульса единицы объема

электромагнитной волны ‌р_w‌ равен:a);

b) плотность энергииравна:b);

c) модуль вектора Пойнтингаравен:c);

d) интенсивность волныI равна: d);

Варианты ответов: A) a-b, b-a, c-c, d-a; B) a-b, b-d, c-d, d-c; * C) a-c, b-d, c-a, d-b; D) a-d, b-a, c-b, d-c;

32. (НТ2). (З). Пусть - вектор Пойнтинга,,-амплитуды напряженности полей у гармонической плоской волны в вакууме. Плотность потока импульса в волне, распространяющейся вдоль осиOZ, равна:

A)т.к. векторнаправлен вдоль*B)т.к.-результат действия силы Лоренца, параллельный*C), т.к.D), т.к

Неверными являются следующие ответы:

33. (НТ1). (З). В результате поглощения электромагнитной волны веществом единичной поверхности среды в единицу времени передается импульс:

A);B);C);D).

Неверные ответы: В, D.

34. (НТ2). (С). Выражению, стоящему в левом столбике, соответствует следующее соотношение, стоящее в правом столбце:

А) Давление света на вещество в результате его поглощения равно		А)
В) Давление электромагнитной волны на вещество при полном отражении равно		В)
С) Вектор импульса, переносимый единицей объема волны равен		С)
D) Интенсивность волны равна		D)

Ответ: A-D; B-C; C-A; D-B.

35.(HТ2). (З). Если при попадании в вещество свет сначала испытывает рассеяние и поглощается уже рассеянный свет, то давление света:

*A) останется таким же как и в отсутствие рассеяния;

B), т.к. в каждом акте рассеяния будет передаваться импульс, больший чем при поглощении;

C), поскольку излучение будет постепенно поглощаться;

D) в зависимости от соотношения между расстоянием и поглощением возможны все три варианта.

36. (НТ1). (З). Если умножить амплитуду магнитного поля на удельное сопротивление вакуума, то получим:

*А) напряженность поля Е_m;

В) энергию, запасенную в магнитном поле;

С) значение вектора магнитной индукции;

D) интенсивность волны.

37. (НТ2). (З). Если интенсивность электромагнитной волны равна, то значение амплитуды электрического поля в волне:

А) не может быть никогда;

*В) будет в диэлектрике с ;

С) возможно если пучок электромагнитных волн дефокусировать;

D) возможно в среде, где волна испытывает случайное рассеяние.

38. (НТ1). (З). Общая формула для фазовой скорости упругих волн в жидкостях и газах равна:

А) ; В); * С);D)

39. (НТ2). (З). Простейшей моделью твердого тела является цепочка атомов, связанных между собой квазиупругими силами. На рисунке приведена для цепочки атомов зависимость

ω от kдля упругих волн. Из рисунка следует, что волны:

А) не обладают дисперсией;

* В) дисперсия нормальная;

С) дисперсия аномальная;

D) по кривым нельзя определить вид дисперсии

40. (НТ1). (З). Дисперсионные соотношения для цепочки квазиупруго связанных атомов имеют вид . Из уравнения следует, что волны в цепочке:

А) не обладают дисперсией;

* В) дисперсия нормальная;

С) дисперсия аномальная;

D) по формуле нельзя однозначно определить вид дисперсии.

41. (НТ1). (З). Дисперсионные соотношения для цепочки квазиупруго связанных атомов имеют вид . Из уравнения следует , что дисперсия отсутствует при:

*А) 0 В)С)D)

42. (НТ2). (З). Для упругой волны выражениям, стоящим в левом столбце, соответствуют следующие соотношения из правого:

a) плотность кинетической энергииwк b) плотность потенциальной энергииwп c) вектор Умова d) интенсивность волныI

a) b) c) d)

Варианты ответов:

A) a-a, b-a, c-d, d-c; B) a-a, b-b;

C) a-d, b-b, d-c; *D) a-b, b-b, c-d, d-c.

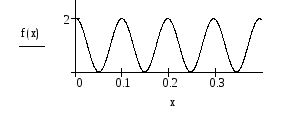
43. (НТ2). (З). На рисунке представлен мгновенный снимок, плоской бегущей вдоль оси ОХ, звуковой волны. Распределение значений вектора Умова в пространстве имеет вид

A)

т.к. W_kиW_n частиц изменяются в противофазеB)

W_kиW_n синфазныW_kиW_nтам где*C)

W_kиW_nсинфазны их максимумы приD)

т.к. поток энергии периодически изменяет направление

44. (НТ2). (З). На рисунке представлен мгновенный снимок скорости смещения частиц в упругой волне. Распределение значений вектора Умова в пространстве имеет вид:

A)т.к.W_kиW_n частиц изменяются в противофазе

*B)W_kиW_n синфазныW_kиW_nтам гдеC)W_kиW_nсинфазны их максимумы при

D)т.к. поток энергии периодически изменяет направление

45. (НТ1). (З). В металлической пластине в направлении, перпендикулярном ее границе, возбуждают продольную или поперечную упругие волны одинаковой амплитуды. Падая на границу с воздухом, волна:

*А) не возбуждает в воздухе волну, если она поперечная;

В) и поперечная и продольная волны возбуждают одинаковую волну;

С) поперечная волна возбуждает волну малой интенсивности;

D) эффективность возбуждения зависит от отношения коэффициентов сдвиговой деформации (G) и модуля Юнга. Привозбуждение более эффективно поперечной волной.