
- •1. С помощью алгоритма Дейкстры найти путь минимального веса между вершинами s и t в нагруженном графе.
- •Решение
- •2. Найти максимальный поток в заданной транспортной сети, используя алгоритм Форда-Фалкерсона. Проверить ответ по теореме Форда-Фалкерсона (найти минимальный разрез графа сети).
- •Решение
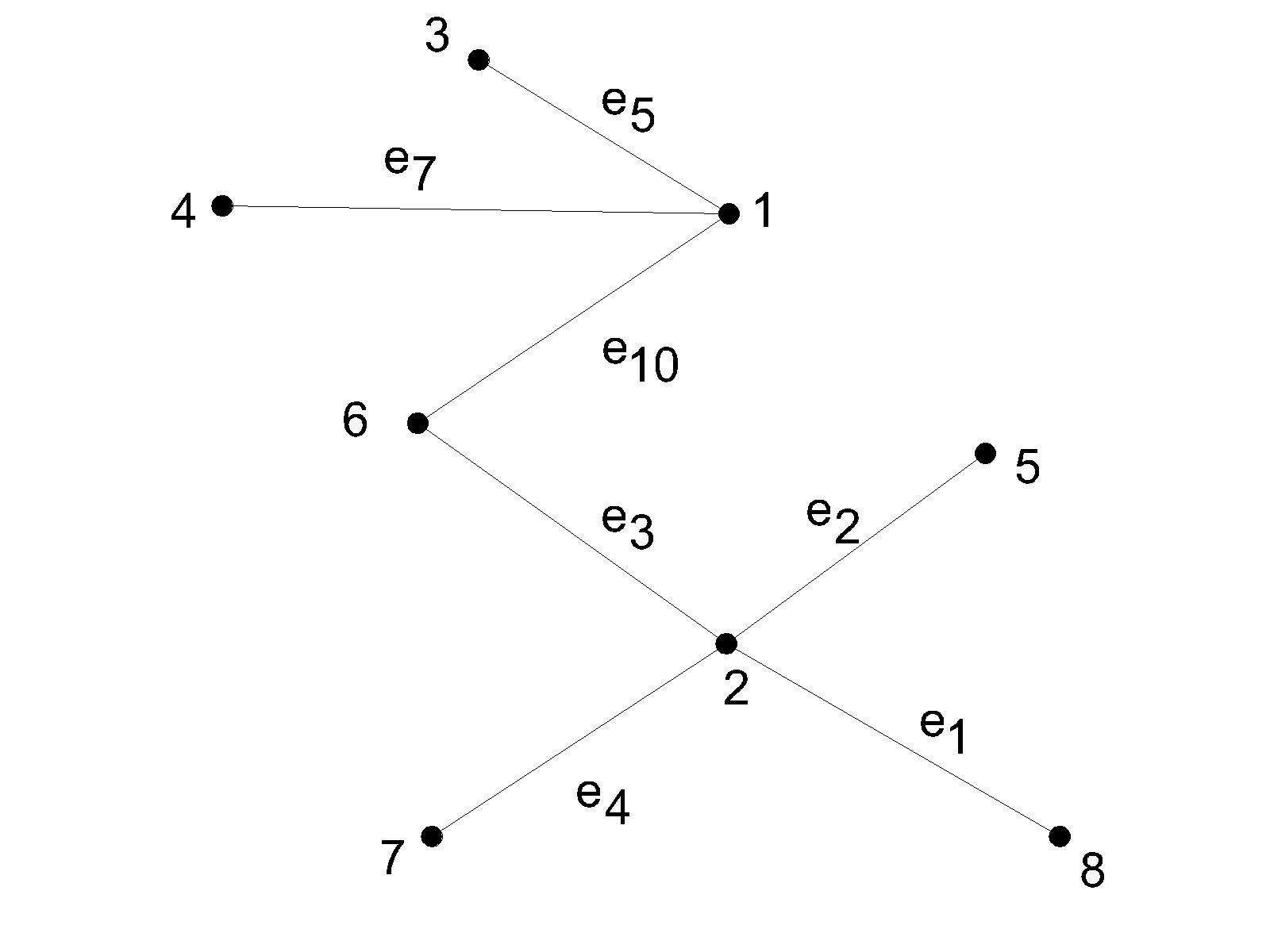
- •3. По матрице инцидентности построить остовное дерево графа. Составить список ветвей и хорд графа. Построить граф.
- •Решение
- •4. А) Написать таблицу состояний данного автомата.
Решение
Построим сам граф. Столбцы – вершины графа, строки – его рёбра. Если ребро инцидентно вершине, то клетка будет закрашена. Получим:

Составим остовное дерево для данного
графа. Остовное дерево графа – это
подграф графа, состоящий из всех вершин
графа и минимального числа рёбер так,
чтобы из любой вершины можно добраться
в любую. Сначал включаем в оствное дерево
ребро ![]() Ребро
Ребро ![]() добавляет к остовному дереву вершину
добавляет к остовному дереву вершину
![]() ,
его также включаем. Ребро
,
его также включаем. Ребро ![]() добавляет к остовному дереву вершину
добавляет к остовному дереву вершину
![]() ,
его также включаем. Ребро
,
его также включаем. Ребро ![]() добавляет к остовному дереву вершину
добавляет к остовному дереву вершину
![]() ,
его также включаем. Ребро
,
его также включаем. Ребро ![]() добавляет к остовному дереву вершину
добавляет к остовному дереву вершину
![]() ,
его также оставляем. Ребро
,
его также оставляем. Ребро ![]() добавляет к остовному дереву вершину
добавляет к остовному дереву вершину
![]() ,
его также оставляем. Ребро
,
его также оставляем. Ребро ![]() не добавляет к остовному дереву новых
вершин, поэтому его в остовное дерево
не включаем. Ребро
не добавляет к остовному дереву новых
вершин, поэтому его в остовное дерево
не включаем. Ребро ![]() добавляет к остовному дереву вершину
добавляет к остовному дереву вершину
![]() ,
поэтому его также включаем. В остовное
дерево включены все вершины графа,
поэтому остовное дерево построено.
,
поэтому его также включаем. В остовное
дерево включены все вершины графа,
поэтому остовное дерево построено.
4. А) Написать таблицу состояний данного автомата.
б) Считая автомат неинициальным, построить эквивалентный автомат Мура. Проверить работу данного и построенного автоматов над одним и тем же словом.

Решение.
Изобразим таблицу данного автомата
|
A\Q |
1 |
2 |
3 |
4 |
|
a |
1,0 |
4,1 |
1,0 |
2,1 |
|
b |
3,1 |
3,1 |
4,0 |
4,0 |
По данному неинициальному автомату
Мили
![]() строим эквивалентный ему автомат Мура
строим эквивалентный ему автомат Мура
![]() следующим образом:
следующим образом:
Автомат
![]() содержит
содержит
![]() состояний, каждое из которых мы будем
помечать двумя символами. Состояния
автомата
состояний, каждое из которых мы будем
помечать двумя символами. Состояния
автомата
![]() обозначим так:
обозначим так:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
|
μ |
- |
- |
- |
- |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
|
A\Q |
*1 |
*2 |
*3 |
*4 |
a1 |
b1 |
a2 |
b2 |
a3 |
b3 |
a4 |
b4 |
|
a |
a1 |
a2 |
a3 |
a4 |
a1 |
a3 |
a4 |
a3 |
a1 |
a4 |
a2 |
a4 |
|
b |
b1 |
b2 |
b3 |
b4 |
b1 |
b3 |
b4 |
b3 |
b1 |
b4 |
b2 |
b4 |
Проверим работу исходного автомата над
словом
![]() ,
запустив его из 2 состояния:
,
запустив его из 2 состояния:
3
1
1
3
1
0
Построенный автомат Мура запускаем из
состояния
![]()
0 a3 a1 b1 a3
Как видим, результаты обоих автоматов совпали.


