Контрольные вопросы и задачи

1. Что называют абсолютной, относительной и приведенной погрешностью?

2. Определить абсолютную погрешность амперметра класса точности 1,5 с пределом измерения .

3. Определить абсолютную погрешность вольтметра класса точности 1,5 с пределом измерения .

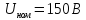4. Какие существуют классы точности измерительных приборов и что они означают?

5. Способы расширения пределов измерения амперметров и вольтметров магнитно-электрической системы?

6. Определить сопротивление шунта для измерения тока до I=10А измерительным механизмом с внутренним сопротивлением R=10 Ом и номинальным током I_Н = 7.5мА.

7. Определить добавочное сопротивление к измерительному механизму (R=10 Ом, I_Н = 7,5мА) для измерения напряжения до 150В.

8. Перечислите существующие методы измерения напряжений и сопротивлений, и какие из них применяются в данной работе?

Литература

1. Касаткин, А.С. Электротехника / А.С. Касаткин, М.В. Немцов.- М.: Изд - во «Академия».- 2005.- С. 4-20.

Лабораторная работа 2

Неразветвленная электрическая цепь синусоидального тока с активно-реактивными сопротивлениями. Резонанс напряжения

Цель работы:

Исследование неразветвленной электрической цепи синусоидального тока при наличии потребителей с различным характером сопротивлений, определение параметров цепи, установление условий резонанса напряжений.

Сведения из теории

Полное сопротивление последовательной цепи в комплексной форме:

z = r + j∙xL– j∙xC= r+ j∙(xL-xC),

(2.1)

где x_L = ωL – реактивное индуктивное сопротивление;

x_C = 1/ ωC – реактивное емкостное сопротивление.

Треугольник сопротивлений:

(2.2) (2.3)

Активная и реактивная мощность в последовательной цепи определяются по формулам:

P = I2∙r, Q = I2∙x.

(2.4) (2.5)

Комплекс полной мощности равен:

.

(2.6)

Коэффициент мощности потребителя показывает, какая часть полной мощности, передаваемой от источника, используется приемником в качестве активной мощности.

.

(2.7)

Величину cosφ в большинстве случаев увеличивают для уменьшения потерь электроэнергии.

Резонанс напряжения наблюдается в последовательной электрической цепи. Закон Ома для этой цепи

.

(2.8)

При резонансе напряжений ωL= 1/ωC. Поскольку реактивные сопротивления взаимно компенсируются, угол сдвига фаз между током и напряжением φ =0 и “Z” минимально.

Векторная диаграмма напряжений и токов последовательной цепи при резонансе напряжений показана на рис. 2.1

Рис. 2.1 Векторная диаграмма токов и напряжений для случая резонанса напряжений

Частотным характеристикам называются зависимости тока, напряжений, сопротивления от частоты источника.

Величина потребляемого из сети тока при резонансе напряжений достигает наибольшего значения, что используется для определения резонансной частоты. Резонанс напряжений можно получить путем изменения параметров цепи L, C или частоты. При резонансе свойства последовательной цепи характеризуются величиной добротности резонансного контура Q =ρ/r, где

.

(2.9)

Резонанс напряжений используется для настройки контуров в автоматике и радиотехнике.
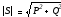