1. Введение

1.1. Тела с радиальной симметрией (шары, цилиндры, колёса и т. п.) обладают свойством катиться по твёрдой поверхности. Такое свойство обеспечивается тем, что точки катящегося тела, соприкасающиеся с опорной (твёрдой) поверхностью, на мгновение "сцепляются" с этой поверхностью. Сцепление обусловлено электрическими силами межмолекулярного взаимодействия между точками тела и поверхности, по которой оно катится. При полном сцеплении оказывается, что скорости точек тела, контактирующих с поверхностью, должны быть равны скоростям точек поверхности, которая обычно считается неподвижной в заданной системе отсчёта.

Эти точки катящегося тела называются мгновенными центрами

скоростей (м.ц.с.). Через них в каждое данное мгновение проходит неподвижная мгновенная ось, относительно которой катящееся тело совершает "мгновенное вращение", т. е. поворот в том направлении, куда тело движется.

Если сцепления недостаточно, тогда возникает скольжение, и качение тела может полностью прекратиться. Отсутствием сцепления объясняется, например, буксование ведущих колес автотранспорта на мокром глинистом грунте. На твёрдой поверхности при отсутствии сцепления нормальное качение тел также не происходит.

Нормальным качением (качением без скольжения) называется движение тел с радиальной симметрией при наличии мгновенной оси вращения в точках контакта с опорной поверхностью.

Для нормального качения также необходимо, чтобы центр масс тел совпадал с центром симметрии. Если это требование не выполняется, тогда катящееся тело будет периодически отрываться от опорной поверхности ("подпрыгивать"). Это явление изменяет тип движения тела.

1.2. В условиях земного притяжения сцеплению способствует сила тяжести, прижимающая тело к опорной поверхности и обеспечивающая "плотный контакт" между точками тела и поверхности.

Наглядным примером является скатывание по наклонной поверхности. Когда угол наклона плоскости мал, тело катится так же, как и по горизонтальной поверхности. Однако с ростом угла наклона - при некотором предельном угле - тело начинает скользить вдоль поверхности. Качение при большом угле наклона прекращается, так как нормальная (перпендикулярная) к поверхности составляющая силы тяжести уменьшилась настолько, что не обеспечивает сцепления между точками тела и наклонной плоскости.

Ещё пример. Прислоните к вертикальной стенке шарик или, проще, круглый карандаш и отпустите. Качения не возникает, тела будут падать вдоль стенки. Но можно заставить те же тела катиться и по вертикальной поверхности, если прижать их к ней рукой, т. е. обеспечить условие сцепления, о котором говорилось выше.

1.3. Качение тел вдоль вертикального направления в гравитационном поле Земли можно осуществить оригинальным способом, используя для этого намотанную на тело нить (или ленту). Этот способ легко проверить с помощью обычной катушки с нитками. Надо взяться одной рукой за свободный конец намотанной на катушку нити, другой рукой поднять катушку, затем отпустить её, удерживая конец нити на одной высоте. Катушка будет опускаться вниз, разматывая нить. Однако это не обычное (свободное) падение тела.

Катушка, опускаясь вниз, вращается, а если присмотреться внимательно, оказывается, что катушка катится по неподвижной нити, одновременно разматывая её со своей поверхности. В точке схода нити с поверхности катушки расположен мгновенный центр скоростей.

Нетрудно также заметить, что во время опускания катушки нить при сматывании совершает движение вдоль её поверхности, и по этой причине катушка будет крениться то в одну, то в другую стороны. В результате, ориентация тела и мгновенной оси вращения в пространстве оказываются не стабильными, и расчёты движения усложняются.

Примечание. Ориентация тел в пространстве в общем случае характеризуется тремя углами. Разработано несколько способов отсчёта таких углов, определяющих повороты тел в пространстве по отношению к трём взаимно-перпендикулярным осям

В корабельной и авиационной практике используются углы Крылова: угол крена, угол рысканья, угол дифферента (или тангажа- в авиации).

Для многих исследований применяются также углы Эйлера: угол прецессии, угол нутации, угол собственного вращения. Правила отсчёта углов Крылова и Эйлера изучаются в теоретической механике и в специальных курсах.

Ориентация тела при вращении на неподвижной оси характеризуется одним углом, который принято называть углом поворота. Этот угол можно считать идентичным углу дифферента или углу собственного вращения в методах Крылова и Эйлера, если тело совершает повороты только относительно одной оси, не изменяющей ориентации в пространстве.

При качении, в общем случае, тело может изменять направление движения (менять курс) и наклоняться (крениться), совершая одновременно повороты относительно мгновенной оси. При этом мгновенная ось будет также разворачиваться и изменять ориентацию. Для исследования кинематики и динамики такого движения требуется учёт поворотов тела относительно трёх осей, что и приводит к усложнению расчётов.

Расчёты качения тел становятся более простыми, если мгновенная ось остаётся параллельной самой себе, т. е. сохраняет ориентацию в пространстве.

Оптимальная стабилизация положения мгновенной _оси вращения

получается при скатывании по двум нитям. Для этого на тело цилиндрической формы следует намотать две нити, расположив намотку симметричными рядами относительно середины (центра масс) тела.

Схема такой конструкции, разработанной Максвеллом, показана на рис. 1а. Дня проведения опытов один конец каждой нити закрепляют на поверхности цилиндра, другой - на неподвижном кронштейне. Поднятое вверх тело с намотанными на его поверхность нитями - после отпускания -скатывается вниз по двум отвесным нитям. Качение вниз продолжается до тех пор, пока нити не разматываются полностью. После этого тело начнёт подниматься вверх, продолжая катиться по нитям и наматывая их на свою поверхность. 'Это движение "вниз - вверх" многократно повторяется с уменьшающейся высотой подъёма из-за потерь механической энергии.

LLLL LLLL LLLL LLLL LLLL LLLL

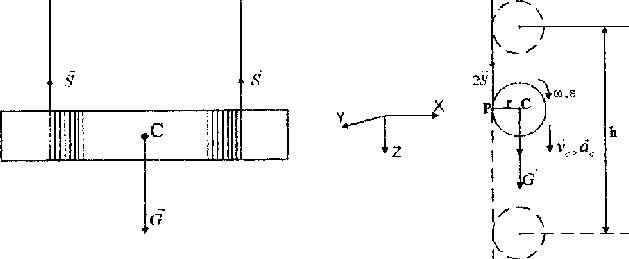
а) схема намотки нитей б) схема для расчётов

Рис. 1.

Движение цилиндра "вверх" с продолжающимся качением по нити объясняется двумя причинами:

1) в нижней точке спуска (когда нить полностью размотана с поверхности тела) вектор импульса центра масс в течение малого интервала времени изменяет свое направление на противоположное. Изменение направления вектора импульса центра масс обеспечивается кратковременным увеличением силы натяжения нити, называемом рывком нити. Во время рывка нити сила натяжения становится больше силы тяжести, и центр масс тела получает начальный импульс для движения "вверх". Однако этого импульса недостаточно для подъёма вверх, который наблюдается в опыте, так как основная часть начальной энергии преобразуется в энергию вращательного движения цилиндра.

2) когда нить полностью размотана, качение цилиндра по нити прекращается. Мгновенная ось вращения исчезает, и вместо неё возникает новая ось, проходящая через точки закрепления нитей на поверхности цилиндра. По отношению к этой оси тело начинает поворачиваться (вращаться), имея начальную угловую скорость, полученную в конце спуска с заданной высоты. За время поворота цилиндра в нижней точке спуска его центр масс движется с ускорением по дуге окружности с радиусом, равным радиусу тела r. Полная длина пути центра масс за время поворота тела равна 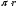. Это время равно времени, в течение которого происходит рывок нити.

Если считать нить абсолютно упругой (т. е. потерь энергии за время рывка нет), то момент импульса цилиндра полностью сохраняется за время поворота в нижней точке спуска, т.е. выполняется закон сохранения момента импульса. Следовательно, угловая скорость вращения тела должна иметь одинаковые величину и направление в конце и в начале рывка нити. По этой причине цилиндр будет наматывать нить на свою поверхность, обладая основным запасом энергии, преобразованной за время спуска в кинетическую энергию вращательного движения.

Примечание. В Приложении 1 дана схема разворота цилиндра в нижней точке спуска, в результате чего происходит переброска нити с изменением направления её дальнейшей намотки при качении "вверх". Там же рассмотрена методика расчёта средней и максимальной сил натяжения при рывке нити.

С учётом названных двух причин и при условии, что потери энергии отсутствуют, по окончании рывка нити цилиндр начинает движение "вверх" со скоростью центра масс и угловой скоростью вращения, имеющими такие же значения, как и в нижней точке предыдущего спуска.

При качении "вверх" снова появляется мгновенная ось вращения. Скорость центра масс и угловая скорость тела уменьшаются (из-за действия силы тяжести и её момента). При отсутствии потерь энергии центр масс должен подняться на ту же высоту, с которой начинался спуск "вниз".

В реальных установках механическая энергия (сумма кинетической и потенциальной энергий) движущегося тела частично преобразуется в другие формы энергии в результате работы непотенциальных (диссипативных) сил: сопротивления среды, трения нитей о поверхность тела, а также в процессе кратковременного рывка нити в нижней точке спуска.

Примечание. При качении тел по твёрдым поверхностям (горизонтальным и наклонным) возникают потери энергии из-за деформаций поверхности катящегося тела и опорной поверхности в точках контакта. Такие деформации являются главным источником сил сопротивления со стороны твёрдых опорных поверхностей. Действие таких сил в механике характеризуется моментом сопротивление качению, величина которого зависит от материала, качества изготовления, температуры и чистоты поверхностей.

В процессе скатывания тел в воздухе по отвесным, упругим, гладким, нерастяжимым нитям потери энергии незначительные. Однако, если изучается возвратное движение "вниз - вверх", то потери энергии увеличиваются и объясняются работой сил неупругих деформаций нитей во время рывка в нижней точке спуска. По этой причине высота подъёма после рывка всегда заметно меньше высоты начального спуска.