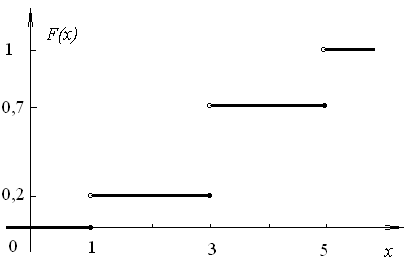-
Функция распределения случайной величины, её свойства, график.
Рассмотрим случайную величину Х, принимающую какие-либо значения. Для любого действительного числа х можно вычислить вероятность события, состоящего в том, что Х примет значение меньше х – P(X<x). Эта вероятность будет зависеть от числа х, т.е. P(X<x) будет функцией от х. Обозначим эту функцию ее через F(x).
Функцией распределения случайной величины Х называется функция F(x), равная вероятности того, что случайная величина Х в результате испытания примет значение, меньшее х:
F(x)= P(X<x).
Функция распределения — самая универсальная характеристика случайной величины, полностью ее задающая. Она является одной из форм закона распределения. Функция распределения может быть задана как для дискретной, так и для непрерывной случайной величины.
Геометрический смысл функции распределения таков: F(x) есть вероятность того, что случайная величина Х в результате испытания примет значение, которое на числовой оси лежит левее точки х.
Свойства функции распределения:
1. Значения функции распределения принадлежат отрезку [0, 1]:
0F(x)1.
Действительно, F(x)= P(X<x), а вероятность P(X<x) [0, 1].
2. F(x) –
неубывающая функция, т.е. если 
>
,
то F(
)F(
).
Доказательство. Пусть 
>
.
Событие, состоящее в том, что Х примет
значение меньшее 
(Х<
),
можно разделить на два несовместных
события:
1) Х
примет значение, меньшее 
с
вероятностью P(X<
);
2) Х
примет значение, лежащее в
полуинтервале 
Х<
с
вероятностью P(
Х<
).
По теореме сложения вероятностей имеем
P(X<
)=P(X<
)+P(
Х<
).
Отсюда
P(X<
)
– P(X<
)=P(
Х<
),
F(
)
– F(
)=P(
Х<
).
Так
как, P(
Х<
)0,
то F(
)–F(
)0.
И, следовательно,
F(
)F(
).
Следствие. Вероятность
того, что случайная величина примет
значение в интервале (
Х<
)
равна приращению функции распределения
на этом интервале:
P(
Х<
)=F(
)
– F(
).
3. На минус бесконечности функция распределения равна 0:
F(–)=0.
На плюс бесконечности функция распределения равна 1:
F(+)=1.
Вспомним, что F(x) есть вероятность того, что случайная величина Х в результате испытания примет значение, которое на числовой оси лежит левее точки х. Будем неограниченно уменьшать значение х, т.е. перемещать точку х по оси Ох влево к –. Попадание при этом случайной точки Х левее х становится невозможным событием, поэтому и вероятность этого события стремится к 0, F(–)=0. Аналогично, неограниченно увеличивая х, перемещая точку х по оси Ох вправо, убеждаемся, что F(+)=1, так как событие X<x становится достоверным.
Таким образом, график функции распределения представляется в виде неубывающей функции, ограниченной прямыми y=0 и y=1.
Зная ряд распределения дискретной случайной величины,
|
X |
|
|
… |
|
|
p |
|
|
… |
|
можно легко вычислить функцию распределения F(x):
F(x)=P(X<x)=
.
Неравенство 
под
знаком суммы указывает, что производится
суммирование тех вероятностей 
,
которые соответствуют значениям 
,
меньшим х.
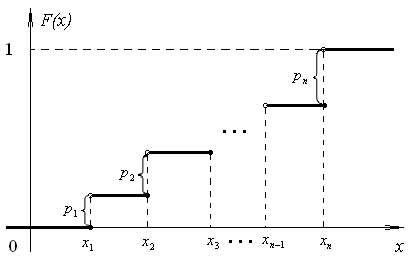
График функции распределения дискретной случайной величины представляет собой разрывную ступенчатую линию, скачки которой происходят в точках, соответствующих значениям случайной величины, и равны вероятностям этих значений. Сумма всех скачковF(x) равна 1.
Общий вид функции распределения дискретной случайной величины приведен ниже:
Пример: Построим функцию распределения для дискретной случайной величины, ряд распределения которой:
|
X |
1 |
3 |
5 |
|
p |
0,2 |
0,5 |
0,3 |
Решение: Если x1, то F(x)=0, так как событие X<x невозможно – величина Х не принимает значений, меньших 1.В полуинтервале 1<x3 только одно значение случайной величины Х=1 удовлетворяет неравенству X<x. Вероятность такого события P(X<x), а следовательно, и функция распределения F(x) равна 0,2.
Если 3<x5, то событие X<x может быть осуществлено двумя способами: когда Х может принимать значение 1 с вероятностью 0,2 и значение 3 с вероятностью 0,5. Эти события несовместны, поэтому F(x)=P(X<x)=0,2+0,5=0,7.
При х5 событие X<x – достоверно. Значит, вероятность P(X<x)=1. F(x)=1.
Итак, функция распределения случайной величины задается следующим образом:
График функции распределения приведен на рисунке ниже.
