14. Интегральная теорема Лапласа.

Теорема: Вероятность того, что в  независимых испытаниях, в каждом из которых вероятность появления события равна , событие наступит не менее  раз и не более  раз, приближенно равна

Здесь

- Функция Лапласа,

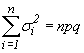   Доказательство. Пусть  - число наступления события A в i-м опыте. Тогда ,  Так как  может принимать только два значения 0 и 1, то для любого i имеем . Кроме того, величина  стремится к бесконечности при . Итак, последовательность случайных величин  удовлетворяет условиям следствия из теоремы Ляпунова. Поэтому сумма этих величин  достаточно больших n имеет распределение, близкое к нормальному, что и требовалось доказать.     Вычислим вероятность того, что случайная величина m, т. е. число наступлений события А в n опытах, удовлетворяет неравенствам , где x1 и x2 - данные числа. Так как a=M(m)=np,  . То согласно формуле получим

Пример. Вероятность того, что деталь не прошла проверку ОТК, равна р = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей. Решение. По условию, р = 0,2; q = 0,8; n = 400; . Воспользуемся интегральной теоремой Лапласа:

.

Вычислим нижний и верхний пределы интегрирования:

Таким образом, имеем

По таблице приложения 2 находим:

Искомая вероятность

15. Относительная частота.

Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой:

W (А) = m / n,

где m - число появлений события, n - общее число испытаний.

Сопоставляя определения вероятности и относительной частоты, заключаем: определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту - после опыта.

Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах, относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Оказалось, что это постоянное число есть вероятность появления события.

Таким образом, если опытным путем установлена относительная частота, то полученное число можно принять за приближенное значение вероятности.

16. Вероятность отклонения относительной частоты от теоритической вероятности.

Вероятность того, что в  независимых испытаниях, в каждом из которых вероятность появления события равна , абсолютная величина отклонения относительной частоты появления события от вероятности появления события не превысит положительного числа , приближенно равна удвоенной функции Лапласа при :

Наивероятнейшее число k₀ появления события A при n независимых испытаниях

(n - число испытаний; p - вероятность появления события при одном испытании).

Пример. Вероятность получения нестандартной детали Р = 0,1. Найти вероятность того, что среди случайно взятых 200 деталей относительная частота появления нестандартной детали отклонится от вероятности Р по абсолютной величине не более чем на 0,03.

Решение. В данном случае П = 200, Q = 0,9, ε = 0,03. По формуле (17.20) имеем

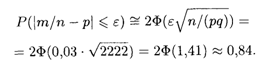
Смысл полученного результата состоит в том, что при доста­точно большом числе проб, каждая из которых содержит 200 случайно выбранных деталей, в 84% случаев отклонение от­носительной частоты от постоянной вероятности Р = 0,1 по абсолютной величине не превысит 0,03.