8. Вероятность появления хотя бы одного события.

Теорема.  Вероятность появления хотя бы одного из событий А₁ , А₂ , ..., А_n , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

Р (A) = 1 — q₁q₂ ... q_n.(*)

Доказательство: Обозначим через А событие, состоящее в появлении хотя бы одного из событий А₁,А₂, ...,A_n. События А и (ни одно из событий не наступило) противоположны, следовательно, сумма их вероятностей равна единице:

Отсюда, пользуясь теоремой умножения, получим

или

Ч а с т н ы й   с л у ч а й. Если события А₁ , А₂ , ..., А_n имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий

P (A) = l — qⁿ. (**)

Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы:p₁ = 0,8; p₂ = 0,7; p₃ = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Р е ш е н и е. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события A₁(попадание первого орудия), А₂ (попадание второго орудия) и A₃ (попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям A₁, А₂ и А₃ (т. е. вероятности промахов), соответственно равны:

q₁ = l — p₁ = l — 0,8 = 0,2; q₂ = l — p₂ = l — 0,7 = 0,3;

q₃ = 1 — p₃ = 1 — 0,9 = 0,l.

Искомая вероятность

P (A) = 1 — q₁q₂q₃ = 1 — 0,2 * 0,3 * 0,1 = 0,994.

9. Формула полной вероятности.

Если событие А может произойти только при выполнении одного из событий , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле:

.

Вновь рассмотрим полную группу несовместных событий , вероятности появления которых . Событие А может произойти только вместе с каким-либо из событий , которые будем называть гипотезами. Тогда по формуле полной вероятности:

10. Вероятность гипотез. Формулы Бейеса.

Имеется полная группа несовместных гипотез . Вероятности этих гипотез до опыта известны и равны соответственно . Произведен опыт, в результате которого наблюдено появление некоторого события .  Здесь, по существу, речь идет о том, чтобы найти условную вероятность  для каждой гипотезы.

Из теоремы умножения имеем:

,

или, отбрасывая левую часть,

,

откуда

.

Выражая  с помощью формулы полной вероятности, имеем:

.

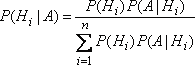
Формула носит название формулы Бейеса или теоремы гипотез.

Пример: Прибор может собираться из высококачественных деталей и из деталей обычного качества; вообще около 40% приборов собирается из высококачественных деталей. Если прибор собран из высококачественных деталей, его надежность (вероятность безотказной работы) за время  равна 0,95; если из деталей обычного качества – его надежность равна 0,7. Прибор испытывался в течение времени  и работал безотказно. Найти вероятность того, что он собран из высококачественных деталей.

Решение. Возможны две гипотезы:

 - прибор собран из высококачественных деталей,

 - прибор собран из деталей обычного качества.

Вероятность этих гипотез до опыта:

.

В результате опыта наблюдено событие  – прибор безотказно работал время .

Условные вероятности этого события при гипотезах  и  равны:

По формуле (3.5.1) находим вероятность гипотезы  после опыта:

.