
- •Основные формулы комбинаторики: размещения, перестановки, сочетания.
- •Формула размещения:
- •Формула сочетания:
- •Виды случайных событий.
- •Виды событий:
- •Теорема умножения вероятностей независимых событий.
- •Условная вероятность. Теорема умножения вероятностей зависимых событий.
- •Вероятность появления хотя бы одного события.
- •Повторение испытаний. Формула Бернулли.
- •Свойства функции Гаусса :
- •Интегральная теорема Лапласа.
- •- Функция Лапласа,
- •Относительная частота.
- •Вероятность отклонения относительной частоты от теоритической вероятности.
- •Случайные величины.
- •Отклонение случайной величины от её математического ожидания.
- •Дисперсия дискретной случайной величины, её свойства.
- •Функция распределения случайной величины, её свойства, график.
- •Плотность распределения вероятностей непрерывной случайной величины, её свойства.
- •Нахождение функции распределения по известной плотности распределения.
- •Нормальное распределение, его математическое ожидание, дисперсия.
- •36. Нормальная кривая.
- •39. Правило трех сигм.
- •40. Генеральная и выборочная совокупность. Повторная и бесповторная выборки. Статическое распределение выборки.
- •41. Понятие о системе случайных величин.
-
Нормальное распределение, его математическое ожидание, дисперсия.
Случайная
величина ![]() называется
распределенной по нормальному закону,
если ее плотность вероятности имеет
вид:
называется
распределенной по нормальному закону,
если ее плотность вероятности имеет
вид:
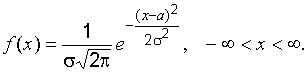
Здесь ![]() математическое
ожидание,
математическое
ожидание, ![]() дисперсия,
дисперсия, ![]() среднее
квадратическое отклонение. Как и
ранее,
среднее
квадратическое отклонение. Как и
ранее, 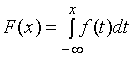 ,
однако, этот интеграл вычисляется
численными методами. Чтобы упростить
эту процедуру, пользуются преобразованием
случайной величины
,
однако, этот интеграл вычисляется
численными методами. Чтобы упростить
эту процедуру, пользуются преобразованием
случайной величины ![]() и
правилом сохранения элемента вероятности
и
правилом сохранения элемента вероятности ![]() ,
где
,
где ![]() плотность
распределения вероятности случайной
величины
плотность
распределения вероятности случайной
величины ![]() :
:
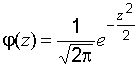 .
.
Как
видим, индивидуальные числовые
характеристики распределения
(математическое ожидание и дисперсия)
в последнее выражение не входят, т.е.
вышеуказанным преобразованием нормальная
случайная величина ![]() приведена
к нормальной стандартной случайной
величине
приведена
к нормальной стандартной случайной
величине ![]() с
параметрами 0 (математическое ожидание)
и 1 (дисперсия). Дифференциальная и
интегральная функции стандартного
нормального распределения табулированы
(имеются таблицы), что существенно
облегчает вычисления. Интегральная
функция распределения обозначается
с
параметрами 0 (математическое ожидание)
и 1 (дисперсия). Дифференциальная и
интегральная функции стандартного
нормального распределения табулированы
(имеются таблицы), что существенно
облегчает вычисления. Интегральная
функция распределения обозначается ![]() ,
,
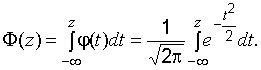
Часто используют функцию Лапласа:
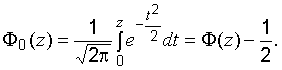
Очевидны следующие свойства:
![]()
![]()
где ![]() .
.
Пример.
Нормальная
случайная величина ![]() задана
математическим ожиданием
задана
математическим ожиданием ![]() и
средним квадратическим отклонением
и
средним квадратическим отклонением ![]() .
Записать соответствующую дифференциальную
функцию, схематично изобразить ее
график, вычислить вероятность попадания
случайной величины
.
Записать соответствующую дифференциальную
функцию, схематично изобразить ее
график, вычислить вероятность попадания
случайной величины ![]() в
интервал
в
интервал ![]()
Решение:
Записать дифференциальную функцию
нормальной случайной величины ![]() с
заданными значениями математического
ожидания и дисперсии значит в общее
выражение для дифференциальной функции
нормальной случайной величины подставить
заданные
с
заданными значениями математического
ожидания и дисперсии значит в общее
выражение для дифференциальной функции
нормальной случайной величины подставить
заданные ![]() и
и ![]() .
Например, если
.
Например, если ![]() ,
то получим
,
то получим
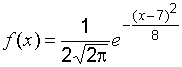 .
.
При
изображении этой функции на схематичном
графике следует учесть, что эта функция
имеет максимум при ![]() ,
симметрична относительно
,
симметрична относительно ![]() (это
видно непосредственно из приведенной
выше формулы) и стремится к нулю при
(это
видно непосредственно из приведенной
выше формулы) и стремится к нулю при ![]() .
Однако правило
.
Однако правило![]() (вероятность
того, что случайная величина примет
значение, по модулю отличающееся от
математического ожидания на
(вероятность
того, что случайная величина примет
значение, по модулю отличающееся от
математического ожидания на ![]() или
более, пренебрежимо мала – составляет
всего около 0,0027) позволяет нам закончить
правую ветвь в точке
или
более, пренебрежимо мала – составляет
всего около 0,0027) позволяет нам закончить
правую ветвь в точке ![]() а
левую – в точке
а
левую – в точке ![]() Высота
максимума в точке
Высота
максимума в точке ![]() составит
составит 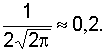 Дополнительно
надо учесть, что перегибы ветвей будут
иметь место в точках
Дополнительно
надо учесть, что перегибы ветвей будут
иметь место в точках ![]()
Вероятность
попадания случайной величины ![]() в
интервал
в
интервал ![]() вычислим
так:
вычислим
так:
![]()
При
этом следует воспользоваться таблицами
функции стандартного нормального
распределения ![]() или
функции Лапласа
или
функции Лапласа ![]() .
.
36. Нормальная кривая.
Центральная предельная теорема. Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.
Говорят,
что случайная величина Х распределена
по нормальному
закону с
параметрами а и ![]() ,
если плотность распределения вероятностей
имеет вид:
,
если плотность распределения вероятностей
имеет вид:
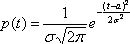 ,
–¥<t<¥.
,
–¥<t<¥.
Вероятностный
смысл параметров а и ![]() таков: а –
математическое ожидание случайной
величины Х, s –
среднее квадратическое отклонение
величины.
таков: а –
математическое ожидание случайной
величины Х, s –
среднее квадратическое отклонение
величины.
Иногда
такой закон распределения
называют Гауссовским. График плотности
нормального распределения называют
нормальной кривой (кривой Гаусса). На
рисунке изображены нормальные кривые
с параметрами а=1
и ![]() ,
, ![]() ,
, ![]() .
.
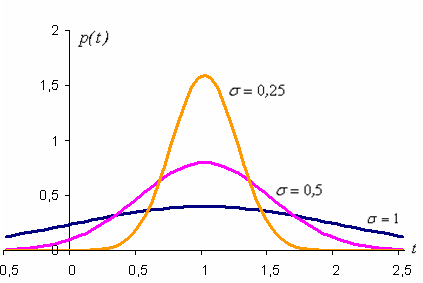
Из
рисунка видно, что положение пика кривых
определяется параметром а=1,
а параметр s (среднее квадратическое отклонение)
характеризует форму нормальной кривой.
При увеличении s уменьшается
максимум кривой распределения, сама
кривая становится более пологой,
растягиваясь вдоль оси абсцисс. И,
наоборот, при уменьшении s возрастает
максимум кривой распределения, сама
кривая становится более «островершинной».
Площадь, ограниченная любой нормальной
кривой и осью абсцисс, равна единице.
Параметр а(математическое
ожидание величины) определяет положение
максимума на оси абсцисс, не влияя на
форму кривой. На рисeyrt
ниже показаны нормальные кривые с
одинаковым средним квадратическим отклонением ![]() и
разными математическими
ожиданиями а=–1, а=0, а=1.
и
разными математическими
ожиданиями а=–1, а=0, а=1.
![]()
![]()
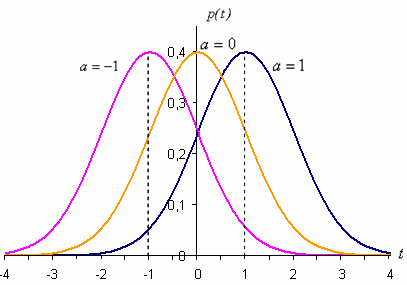
Нормальное
распределение с параметрами а=0
и ![]() называется нормированным.
называется нормированным.
-
Вероятность попадания в заданный интервал нормальной случайной величины.
Вероятность того, что Х примет значение, принадлежащее интервалу (α,β)
P(α<X<β)=Ф((β-a)/σ)-Ф((α-a)/σ),
где
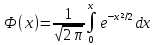 – функция Лапласа.
– функция Лапласа.
-
Ф(-∞)=0
-
Ф(+∞)=1
-
Ф(-х)=1-Ф(х)
P(mx-l<x<mx+l)=Ф(l/σ)-Ф(-l/σ)=2Ф(l/σ)-1
38. Вычисление вероятности заданного отклонения.
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины Х по абсолютной величине меньше заданного положительного числа d, т. е. требуется найти вероятность осуществления неравенства |x —а|<d.
Заменим это неравенство равносильным ему двойным неравенством
![]()
Тогда получим:
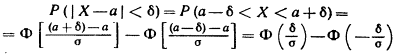
Приняв во внимание равенство:
![]()
(функция Лапласа—нечетная), окончательно имеем
![]() Вероятность
заданного отклонения равна
Вероятность
заданного отклонения равна
![]()
На рисунке наглядно показано, что если две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (-d,d),больше у той величины, которая имеет меньшее значение d. Этот факт полностью соответствует вероятностному смыслу параметра s .
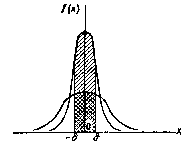
Пример. Случайная величина Х распределена нормально. Математическое ожидание и среднее квадратическое отклонение Х соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.
Решение: Воспользуемся формулой
![]()
По условию ,
![]()
тогда
![]()
