1. Свойства газовой смеси

1.1. Молекулярный вес смеси газов и газовая постоянная смеси

; (1.1)

.

1.2. Плотность смеси газов по уравнению Менделеева-Клайперона

. (1.2)

1.3. Объемные доли компонент

; ;;;; (1.3)

Проверка: 0,390 + 0,149 + 0,133 + 0,328 = 1,000

1.4. Расчет коэффициента кинематической вязкости смеси.

Коэффициент динамической вязкости компонент по формуле Сазерленда при атмосферном давлении и температуре Т = 353 К

; ; (1.4)

; ;.

Коэффициент динамической вязкости смеси при давлениях, близких к атмосферным, в соответствии с нормативными документами [1] вычисляется по формуле Чепмена-Энскога (метод Уилки)

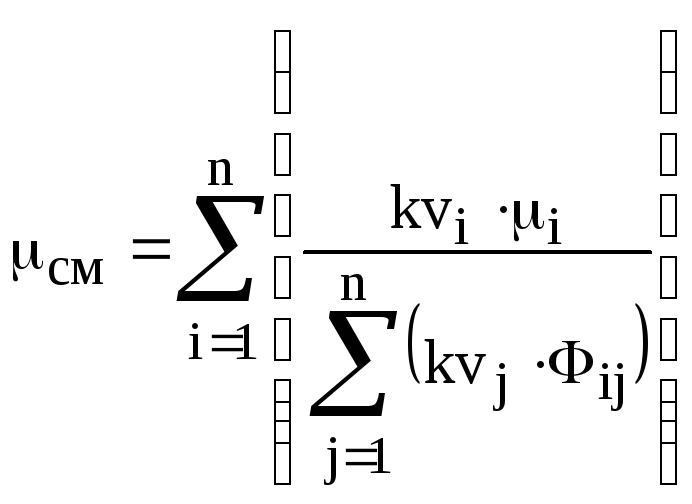; . (1.5)

;

; .

2. Расчет течения в простом трубопроводе

Рис. 27. Гидравлическая схема простого трубопровода

2.1. Режим течения в простом трубопроводе

При закрытых вентилях В, С получаем простой трубопровод (без ветвлений), схема которого показана на рис. 27. Эквивалентный диаметр трубопровода

. (2.1)

Средняя скорость течения газовой смеси в трубопроводе и число Рейнольдса

; . (2.2)

Число Рейнольдса много больше критического значения (2300), значит, в трубопроводе турбулентный режим течения.

2.2. Уравнение Бернулли для течения в простом трубопроводе

Принимаем в качестве исходного сечения – вход в воздухозаборное устройство, конечное – сечение трубы на уровне вакуумметра. Заметим, что конечное сечение выбирается обязательно ниже начального по течению. Запишем уравнение Бернулли

. (2.3)

где р_н, р_к– давление в начальном и конечном сечениях,

V_н, V_к – скорости в начальном и конечном сечениях,

- сумма потерь давления на трение по длине трубопровода,

- сумма потерь давления в местных сопротивлениях,

- разность давлений, обусловленная гидростатическим напором.

При турбулентном течении коэффициенты Кориолиса принимаются . Абсолютное давление в начальном и конечном сечении р_н= р_атм, р_к= р_атм - р_V.

Разность давлений, обусловленная гидростатическим напором,

, (2.4)

где - геометрический напор в начальном и конечном сечениях, Геометрический напор представляет собой вертикальную координату центра тяжести соответствующего сечения. В качестве оси сравнения выбираем ось нижней трубы. Тогдаz_к = 2Н, z_н = 0. - плотность воздуха при атмосферном давлении и температуре наружного воздуха; при 15ºС получим

,

.

2.3. Расчет потерь давления

Потери давления на трение по длине трубопровода вычисляются по формуле Дарси-Вейсбаха. Для трубопровода с постоянной площадью сечения

. (2.5)

Так как Re > 4000, коэффициент потерь на трение можно найти по формуле Альтшуля

; (2.6)

.

Потери давления в местных сопротивлениях

. (2.7)

Коэффициент потерь в вентиле задан; в повороте на 90º принимаем ζ_вп = 1,3.

Коэффициент потерь в воздухозаборном устройстве находим по формуле для плавного сужения потока (конфузора)

; ;. (2.8)

Коэффициент найдем по средним значениям скорости и эквивалентного диаметра в воздухозаборном устройстве

; ;;;.

Откуда

.

Видно, что последний коэффициент много меньше предыдущих коэффициентов ζ_вп, ζ_вент , и им можно пренебречь. Вычислим сумму потерь давления в местных сопротивлениях по формуле (2.7)

.

2.4. Расчет показаний вакуумметра

Выразим p_V из уравнения Бернулли (2.3)

; (2.9)

.