МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Марийский Государственный Технический Университет

Факультет информатики и вычислительной техники

Кафедра ИВС

Лабораторная работа №5

"Трехфазная цепь при соединении нагрузки звездой"

по дисциплине “Электротехника”

Выполнил: студент группы ИВТ-11

Павлов А. Л.

Проверил: доцент кафедры ИВС

Берман Н.В.

Йошкар-Ола, 2013

Содержание

1. Теоретическая часть………………………………………………………3)

2. Практическая часть………………………………………………………..5)

3. Программа работы………………………………………………………...9)

4. Вывод…………………………………………………………………......15)

5. Список литературы………………………………………………………16)

Теоретическая часть

Цель работы. Уяснить основные соотношения между напряжениями и токами трехфазной цепи в симметричном и несимметричном режимах при соединении нагрузки звездой с нулевого и без нулевого провода, а также научиться строить векторные диаграммы для различных видов нагрузки.

Пояснения. Трехфазной цепью с симметричной системой гармонических напряжений генератора называют цепь, состоящую из трех электрически связанных фаз (А,В,С), в каждой из которых действуют одинаковые частоте и амплитуде гармонические ЭДС, сдвинутые относительно друг друга на треть периода или на 120 :

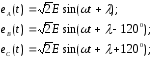
или в комплексной форме:

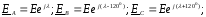
Эти ЭДС называют фазными. Напряжения между фазами называют линейными, которые также образуют симметричную систему:

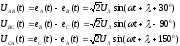
где 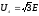или в комплексной форме:

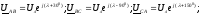
Симметричный режим трехфазной цепи характеризуется симметричной системой фазных и линейных ЭДС, напряжений и токов и возможен при равенстве комплексных сопротивлений фаз: 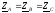. Если комплексные сопротивления фаз различны, то режим будет несимметричным.

На рис.1,а приведен пример трехфазной цепи с нулевым проводом () при соединении нагризки () звездой. Для такой цепи напряжение между нейтралями определяется

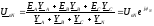
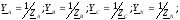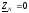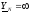
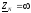где - зависимости фаз и нулевого провода, причем если, тои , а если нулевой провод отсутствует, тои.

При известном напряжении расчет фазных напряжений трудно

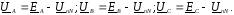
Линейные токи равные фазным токам определяются так

причем ток нулевого провода равен

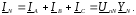
На рис.1,б показаны лучевая векторная диаграмма токов и топографическая векторная диаграмма напряжений для цепи рис.1,а в несимметричном режиме, когда фазные ЭДС симметричны, а сопротивление фаз различны: 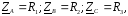причем.

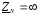а) б)

Рис.1

Схемы исследуемых трехфазных цепей и их графы представлены на рис.2 и 3.

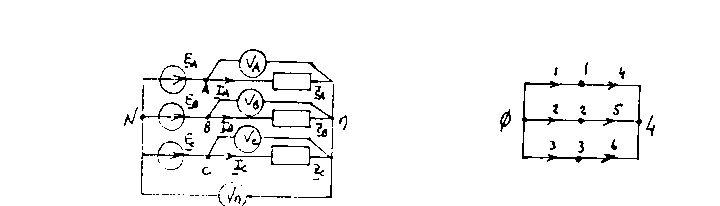
а) б)

Рис.2

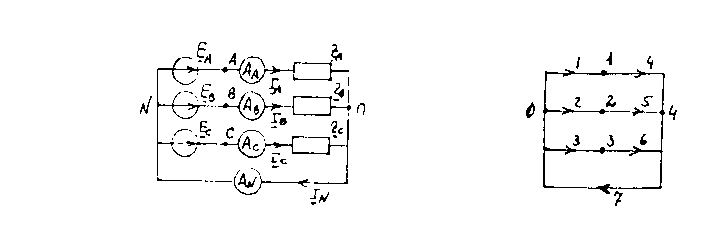
а) б)

Рис.3

В цепях рис.2 и 3 используется вольтметры и амперметры, фиксирующие действующие значения измеряемых величин.

Практическая часть

Исходные данные: U = 380 B, R = 230 Ом, α = 90⁰, β = -30⁰, γ = 210⁰.

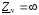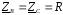1. Для схемы рис.2а (без нулевого провода) при ивыведем формулы для расчета комплексов действующих значений напряжений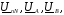и для случаев:

а) ;;

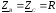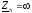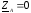
E_a = E*e^iα = 380i

E_b = E*e^iβ = 329,09-190i

E_c = E*e^iγ = -329,09-190i

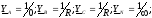
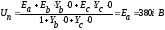
_{Ua = Ea - Un = 0 В}

_{Ub = Eb - Un = 329,09-570i; |Ub|= 658.179 В}

_{Uc = Ec - Un = -329,09-570i; |Uc|= 658.179 В}

_{Ia = Ua * Ya= 0 А}

_{Ib = Ub * Yb =(329.09-570i)*4.348*10-3=1.441-2.497i; |Ib|= 2,883 А}

_{Ic = Uc * Yc = -1,441-2,497i; |Ic|= 2.883 А}

б) ;;

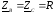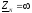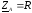
U_a = E_a - U_n = 380i В; |U_а|= 380 В

U_b = E_b - U_n =329,09-190i; |U_b|= 380 В

U_c = E_c - U_n =-329,09-190i; |U_c|= 380 В

I_a = U_a * Y_a= 1.652i; |I_b|= 1,652 А

I_b = U_b * Y_b = 1.431-0.826i; |I_b|= 1,652 А

I_c = U_c * Y_c = -1.431-0.826i A; |I_c|= 1,652 А

в) ;;

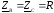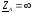
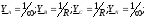
U_a = E_a - U_n = 570i В; |U_a|= 570 В

U_b = E_b - U_n = 329.09; |U_b|= 329.09 В

U_c = E_c - U_n = -329,09; |U_c|= 329,09 В

I_a = U_a * Y_a= 0

I_b = U_b * Y_b = 1,431; |I_b|= 1,431 А

I_c = U_c * Y_c = -1,431; |I_c|= 1,431 А

2. Построим качественные совмещенные топографическую и лучевую векторные диаграммы для напряжений и токов для случаев, указанных в п.1.

Построение векторной диаграммы начинаем с выбора масштаба для напряжения и тока . Откладываем векторы фазных напряжений с учётом их начальных фаз. Соединив вершины полученной звезды фазных напряжений, получаем треугольник линейных напряжений U_ab, U_bc, U_ca. Векторы фазных токов и тока в нейтральном проводе I_a, I_b, I_c, I_n откладываем в масштабе на осях +1, +j.

2. а) б) с)

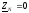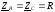3. Для схемы рис.3а при ивыведем формулы для расчета комплексов действующих значений токов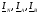для случаев:

а) ;;

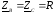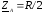
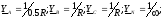
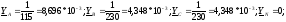
U_a = E_a - U_n = 285i; |U_a|=285 B

U_b = E_b - U_n = 329,09-285i; |U_b|= 435.345 В

U_c = E_c - U_n = -329,09-285i; |U_c|= 435.345 В

I_a = U_a * Y_a= 2,478i; |I_a|= 2,478 А

I_b = U_b * Y_b =1,43-1,2i; |I_b|= 1,87А

I_c = U_c * Y_c = -1,43-1,2i; |I_c|= 1,87 А

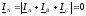
б) ;;;

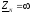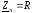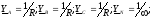
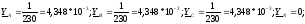
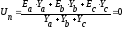
U_a = E_a - U_n =380i; |U_a|= 380 В

U_b = E_b - U_n = 329,09-190i; |U_b|= 380 В

U_c = E_c - U_n = -329,09-190i; |U_c|= 380 В

I_a = U_a * Y_a=1.65i; |I_a|= 1,65 А

I_b = U_b * Y_b =1,49-0,83i; |I_b|= 1,7 А

I_c = U_c * Y_c =-1,49-0,83i; |I_c|= 1,7 А

в) ;;

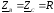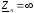
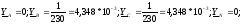
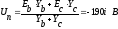
U_a = E_a - U_n = 570i; |U_a|= 570 В

U_b = E_b - U_n = 329.09; |U_b|= 329.09 В

U_c = E_c - U_n = -329,09; |U_c|= 329,09 В

I_a = U_a * Y_a= 0

I_b = U_b * Y_b = 1,43; |I_b|= 1,43 А

I_c = U_c * Y_c =-1,43; |I_c|= 1,43 А

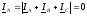
4. Построим качественные совмещенные топографическую и лучевую векторные диаграммы для напряжений и токов для случаев, указанных в п.3.

Построение векторной диаграммы начинаем с выбора масштаба для напряжения и тока . Откладываем векторы фазных напряжений с учётом их начальных фаз. Соединив вершины полученной звезды фазных напряжений, получаем треугольник линейных напряжений U_ab, U_bc, U_ca. Векторы фазных токов и тока в нейтральном проводе I_a, I_b, I_c, I_n откладываем в масштабе на осях +1, +j.

а) б) в)