
Теорема
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров основания на апофему.
Доказательство
Если сторона основания а, число сторон n, то боковая поверхность пирамиды равна:

Где
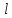 -апофема,
а
-апофема,
а -периметр
основания пирамиды. Теорема доказана.
-периметр
основания пирамиды. Теорема доказана.
Призма
Рассмотрим два разных многоугольника А1А2…An и B1B2…Bn расположенны в параллельных плоскостях α и β так, что отрезки А1B1, А2B2, …, AnBn, соединяющие соответственные вершины многоугольников, параллельны. Каждый из n-четырехугольников
А1А2B2B1, A2A3B3B2, AnA1B1Bn
Является параллелограм, так как имеет попарно параллельные противоположные стороны. Например, в четырехугольнике А1А2B2B1 стороны А1B1 и А2B2 параллельны по условию, а стороны А1А2 и B2B1 по свойству параллельных плоскостей, пересечены третьей плоскостью.
Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных а параллельных плоскостях, и n-параллелограмов, называется призмой.
Многоугольники А1А2…Аn и В1В2…Вn называются основаниями, а параллелограмы – боковыми гранями призмы. Отрезки А1В1, А2В2, AnBn называются боковыми ребрами призмы. Эти ребра как противоположные стороны параллелограмов, последовательно приложенных друг к другу, равны и параллельны.Призму с основаниями А1А2…Аn и В1В2…Вn обозначают А1А2…АnВ1В2…Вn и называют n-угольной призмой.
Перпендикуляр, проведенный из какой-нибуть точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям ,то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна её боковому ребру.
Прямая призма называется правильной, если её основания – правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.
Площадью полной поверхности призмы называется сумма всех её граней, а площадью боковой поверхности призмы – сумма площадей её боковых граней. Площадь Sполн полной поверхности выражается через площадь Sбок боковой поверхноси и площадь Sосн основания призмы форулой
 Sбок+2Sосн
Sбок+2Sосн
Докажем теорему о площади поверхности прямой призмы.
Теорема
Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.
Доказательство
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте h призмы, Площадь боковой поверхности призмы равна сумме площадей указанных прямойгольников, т.е. равна сумме произведений сторон основания на высоту h. Вынося множитель h за скобку, получим в скобках сумму сторон основания призмы, т.е. его периметр Р. Итак, Sбок=Ph. Теорема доказана.
