5 Произведение событий. Условная и безусловная вероятности. Теорема умножения для независимых событий

Произведением двух или нескольких событий называют сложное событие, состоящее в совместном появлении этих событий.

Пусть С — сложное событие, состоящее в совместном появлении событий _. В этом случае пишут

или .

Теорема. Вероятность произведения двух или нескольких независимых событий равна произведению вероятностей этих событий, т.е.

.

Вероятности независимых событий называют безусловными. Зависимые события имеют условные вероятности.

Условной называют вероятность, вычисленную в предположении, что одно или несколько событий уже произошли. Например: — условная вероятность событияА₂, вычисленная в предположении, что произошло событие А₁; — условная вероятность событияА_n, вычисленная в предположении, что произошли события .

6. Условие независимости событий.Теорема умножения вероятностей для независимых событий.

Условие независимости события А₂ от события А₁ записывают в виде , аусловие зависимости — в виде .

Теорема. Вероятность произведения двух или нескольких зависимых событий равна произведению безусловной вероятности одного из этих событий на условные вероятности других, т.е.

.

Задача 1.4. В ящике имеется 25 белых и 36 чёрных шаров. Определить вероятность последовательного появления двух белых шаров при условии, что первый извлечённый шар обратно не возвращается.

Решение. Обозначим события: А₁ — появление первого белого шара; А₂ — появление второго белого шара; С — появление двух белых шаров. Поскольку вероятность события А₂ зависит от того, наступило или не наступило событие А₁, события А₁ и А₂ — зависимые. Применяем теорему умножения вероятностей для зависимых событий, получим

.

Найдём вероятность события А₁:

.

Найдём условную вероятность события А₂ при условии, что событие А₁ наступило:

.

Искомая вероятность равна:

.

7 Теорема сложения для совместных событий

Вероятность суммы двух или нескольких совместных событий A_i определяется по формуле

,

где В — событие, состоящее в появлении хотя бы одного из нескольких совместных событий A_i, а — событие, ему противоположное, состоящее в том, что не появится ни одно из событий A_i,т.е.

.

определяется по формуле , если события A_i независимы, и по формуле , если события A_i зависимы.

8 Многократные испытания. Формула бернулли

Если необходимо определить вероятность того, что при n независимых многократных испытаниях событие А появится ровно k раз, то применяем формулу Бернулли:

,

где — искомая вероятность;p — вероятность появления события А в каждом отдельном испытании (постоянная для всех испытаний); q — вероятность непоявления события А в отдельном испытании (очевидно, что );— число сочетаний изn по k.

;

; ;.

Если k придавать значения от 0 до n (т.е. ), а вероятностивычислять по формуле Бернулли, то получится совокупность вероятностей:, которая носит названиебиномиального распределения вероятностей.

Заметим, что .

Задача 1.5. По одной и той же мишени в одинаковых условиях произведено 3 независимых выстрела. Вероятность попадания в мишень при одном выстреле равна 0,3. Определить вероятности следующих событий:

1. Мишень будет поражена ровно k раз (причём ).

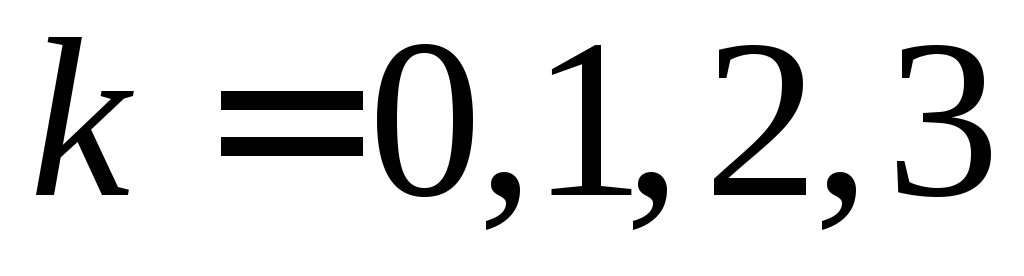Решение: так как ;;;, то имеем:

;

;

;

.

Контроль: 0,34+0,44+0,19+0,03=1,00.

2. В мишени будет не менее двух пробоин:

.

2. Мишень будет поражена не более двух раз:

.

4. Мишень будет поражена хотя бы один раз:

.