3. Вычисление двойного интеграла в полярных координатах

Переход к полярным координатам полезен, когда подынтегральная функция имеет вид ; область интегрированияD есть круг, кольцо или часть таковых.

Рис. 5

Пусть область D ограничена двумя лучами , выходящими из полюса, и двумя кривыми и , где и - однозначные функции при и (рис.5).

Преобразование двойного интеграла от прямоугольных координат x, y к полярным координатам , связанным с прямоугольными координатами соотношениями,, осуществляется по формуле

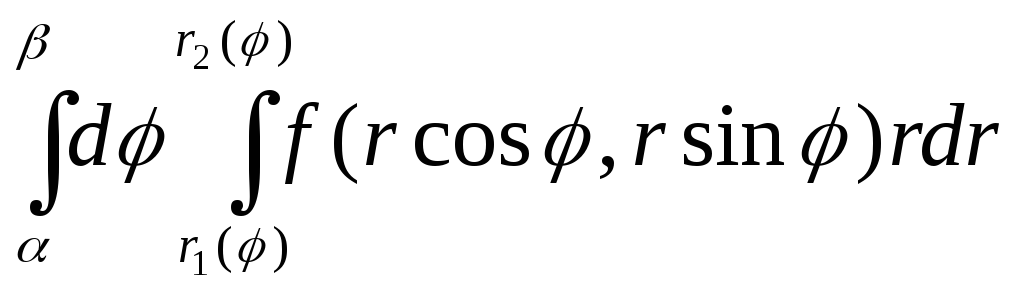= = , (9)

Причем сначала вычисляется интеграл ,в котором считается постоянным.

4. Приложения двойного интеграла

Приведем некоторые примеры применения двойного интеграла.

1. Объем тела,

Объем цилиндрического тела, ограниченного сверху поверхностью z=f(x,y)0, снизу – замкнутой областью D плоскости Oxy, с боков - цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (рис. 1) находится по формуле

V =

(10)

2. Площадь плоской фигуры.

Площадь S области D вычисляется по формуле

S = .

(11)

3. Масса плоской фигуры.

Масса плоской пластинки D с переменой плотностью находится по формуле

m = .

(12)

4. Статические моменты и координаты центра тяжести плоской фигуры.

Статические моменты фигуры D относительно осей Ox и Oy могут быть вычислены по формулам

= и =

(13)

где – переменная плотность; а координаты центра масс фигуры – по формулам

; .

(14)

5. Моменты инерции плоской фигуры.

Моменты инерции плоской фигуры относительно осей Ox и Oy могут быть вычислены по формулам:

= и =

(15)

где – переменная плотность.

Момент инерции фигуры относительно начала координат – по формуле

.

(16)

5. Примеры решения задач

1. Изменить порядок интегрирования (сделать чертеж области).

+ .

Решение.

Повторный интеграл является следствием двойного, поэтому

I = .

Для восстановления области D выписываем из данного повторного интеграла границы области:

y = -2, y = -1, x = , x =0;

y = -1, y = 0, x = .

Построим линии, ограничивающие область.

, следовательно () – уравнение параболы с вершиной в точке (0,-2).

, следовательно () – уравнение параболы с вершиной в точке (0,0) (рис. 6).

Рис. 6

Найдем точки пересечения парабол:

2 + y = – y,

2y = – 2,

y = – 1.

Подставляем в

, но ,

значит .

Производим переход в двойном интеграле к повторному, при этом внешнее интегрирование производим по x, внутреннее – по y. Т.е. возьмем постоянные пределы по переменной x. Для этого спроецируем область D на ось Ox. Проекцией будет отрезок [– 1; 0]. Если провести прямую, параллельную оси Oy (x = const), то она пересекает область D в точках A (назовем ее точкой входа) и B (назовем ее точкой выхода).

Точка A лежит на параболе x² = y + 2 (т.е. y = x² – 2). Точка B лежит на параболе (т.е.y = – x² ).

Получим I = ; инаходим из уравнений соответствующих парабол:

1. точка A лежит на параболе x² = y + 2 (т.е. y = x² – 2), значит , =x² – 2 ;

2. точка B лежит на параболе (т.е.y = – x² ), значит = –x² .

Окончательно получим: I =.

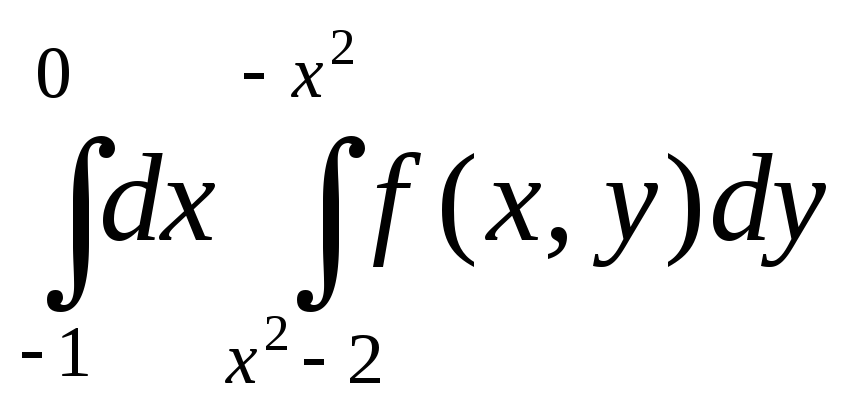Ответ: I =.

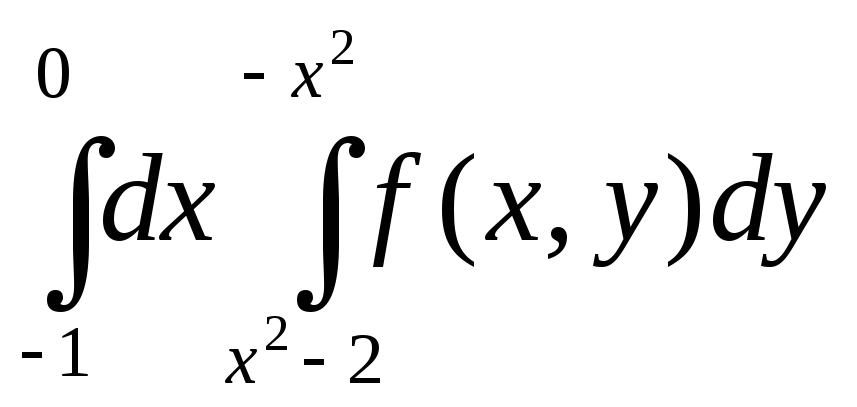2. Вычислить двойной интеграл по области D, ограниченной заданными линиями. Сделать чертеж.

2.1. I =, где область D, ограничена линиями y = x, y = 2x, x = 2, x = 3.

2.2. I =, где область D, ограничена линиями ,y = x .

Решение.

2.1. Изобразим область интегрирования D (рис. 7).

Рис. 7

Область интегрирования принадлежит к виду (4) (см. п.2), тогда

D : ,

.

Вычислим искомый интеграл:

I = =

= =.

Ответ: .

2.2. Изобразим область интегрирования D (рис. 8).

Рис. 8

Область интегрирования принадлежит к виду (4) (см. п.2).

Так как прямая y = x и парабола пересекаются в точкахO(0,0) и A(2,2), то область D определяется системой неравенств:

,

.

Теперь вычислим искомый интеграл:

I == =

==) = =

= .

;

Вычислим = =

dv = dx: v = x.

Применим формулу интегрирования по частям

(17)

=xarctg= =

= .

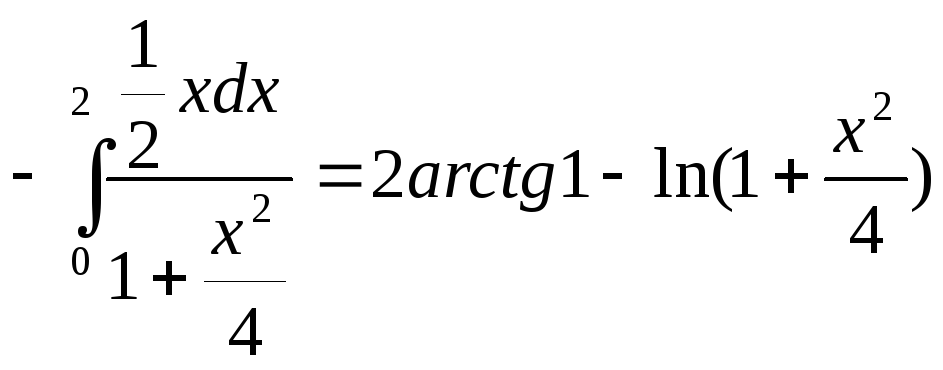
Итак, наш интеграл

I = 2.

Ответ: .

3. С помощью двойного интеграла вычислить площадь фигуры, ограниченной заданными линиями (сделать чертеж):

3.1. , ,y = 3, y = 4.

3.2. : ; (18)

: ; (19)

y = 0, y = x.

Решение.

3.1. Изобразим область интегрирования D (рис. 9).

Рис. 9

Область интегрирования принадлежит к виду (6) (см. п.2).

Выразим x из уравнений и : и.

Тогда область D определяется системой неравенств:

,

.

Для вычисления площади фигуры используем формулу (11).

S = –.

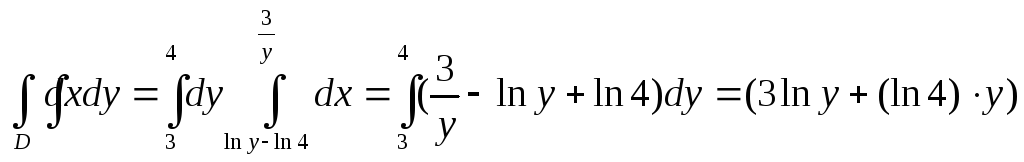
Вычислим

= =

Тогда

S = 1 (кв.ед.).

Ответ: 1 кв.ед.

3.2. Преобразуем данные уравнения окружностей:

–уравнение окружности ( C(1,0), R = 1);

–уравнение окружности ( C(3,0), R = 3).

Изобразим область интегрирования D (рис. 10).

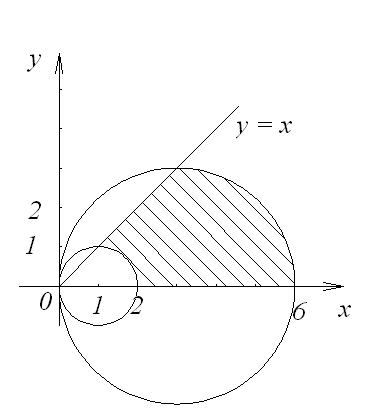
Рис. 10

Т.к. иявляются окружностями, то лучше перейти к полярным координатам.

Переводим уравнения окружностей в полярные координаты, используя формулы: тогда, подставляя соответственно в (16) и (17), получим:

,

,

,

.

,

,

,

.

Область D определяется системой неравенств:

Для вычисления площади фигуры используем формулу (11), а также формулу (9) для преобразования двойного интеграла от прямоугольных координат к полярным.

==

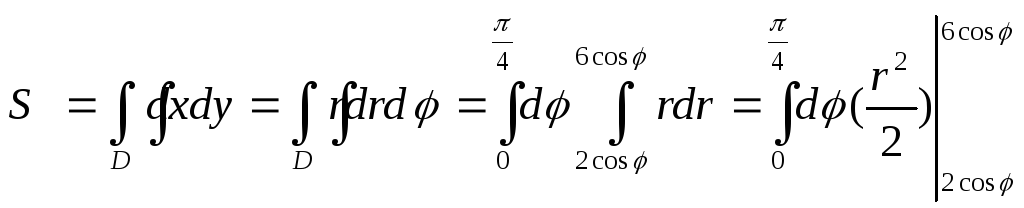= == 8(=.

Ответ: (кв. ед.).