Курсовая работа по ВСТИ
.docxСанкт-Петербургский институт машиностроения (ЛМЗ-ВТУЗ)
Курсовая работа по ВСТИ
Комплексное решение вопросов точности изготовления и контроля сопрягаемых деталей типа “вал-втулка”.
Решение размерной цепи различными методами с целью обеспечения сборки данного узла.
Выполнил: студент группы 4511 Кутузов М. А.
Проверил: Бебнев В. А.
СПБ 2011
Исходные данные
Ø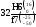
Отверстие: ES=16[мкм]=0.016[мм]; EI=0.
Вал: es=-25[мкм]=0.025[мм]; ei=-50[мкм]=0.05[мм].
Схема полей допусков данного сопряжения
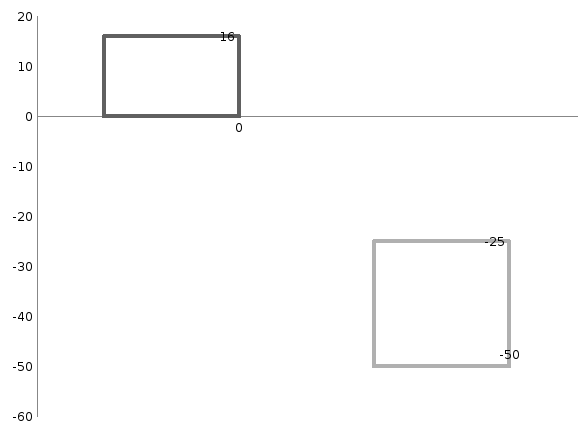
Посадка выполнена с зазором в системе отверстия т.к. поле допуска отверстия находится выше поля допуска вала, а нижнее предельное отклонение отверстия EI=0 и совпадает с нулевой линией сопряжения.
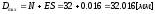
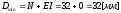
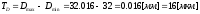
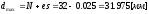
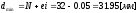
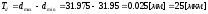
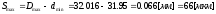- максимальный
зазор
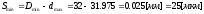- минимальный зазор
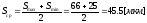- средний зазор
Проектируем рабочий калибр
Для отверстия с номинальным диаметром 32 мм и квалитетом допуска изделия 6 принимаем: H=2.5; y=2; z=2.5 мкм
Схема полей допусков рабочих калибров
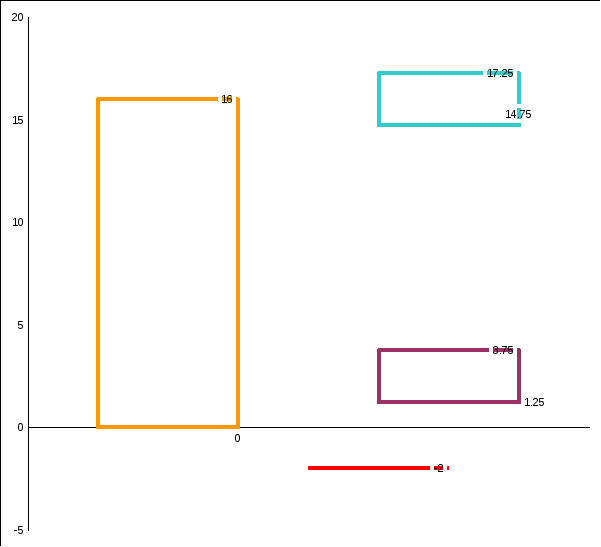
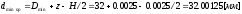
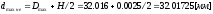
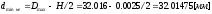
Размеры калибра:
ø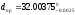
;
ø
;
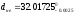ød=24;
;
;
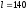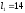Решение размерной цепи различными методами для обеспечения сборки заданного узла.
Решение размерной цепи методом максмумов-минимумов
Исходные данные:
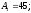
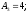
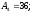
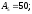
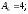
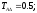мм.
Увеличивающие
звенья:
;
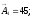
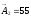мм.
Уменьшающие
звенья:
;
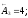
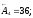
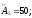
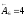мм.
Определяем
номинальный размер
:
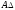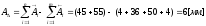
Определяем единицу допуска для размеров 1-500мм:
,
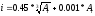мкм
;
;
;
;
;
.
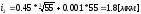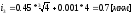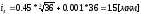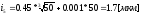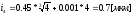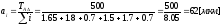, где
-
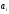средняя ед допуска.
Зная
,
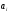определяем квалитет и на основании
таблиц СТ СЭВ 145-75 находим предельные
отклонения на все размеры сопрягаемых
деталей.
Тогда :
ув
звенья:
;
;
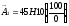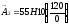ум
звенья:
;
;
;
.
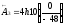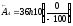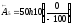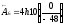Проверяем полученные значения предельных размеров, подставляя в уравнения:
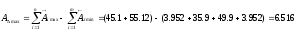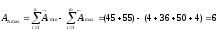[мм]
[мм]
Отсюда
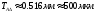совпадает с данным полем допуска,
следовательно выбранные предельные
отклонения нам подходят.
Решение размерной цепи теоретико-вероятностным методом.
Исходные данные:
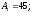
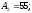
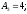
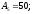
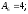
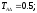мм.
Увеличивающие
звенья:
;
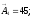
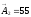мм.
Уменьшающие
звенья:
;
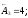
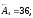
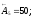
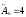мм.
Определяем
номинальный размер
:
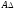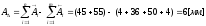
Определяем
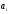из зависимости:
,
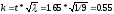где k
– коэф. относительного рассеивания;
t = 1.65 – коэф. зависящий от выбранного процента риска p=10%;
λ – коэф. учитывающий характер закона распределения случайных величин (закон Гаусса)