
Порядок старшей производной определяет порядок системы (звена) в целом.
Если n=1 – система первого порядка; n=2 – система второго порядка.
Передаточной функцией системы от данного входы к данному выходу – отношение изображения по Лапласу выходной переменной к изображению по Лапласу входной переменной при нулевых условиях и равенстве нулю прочих входов.
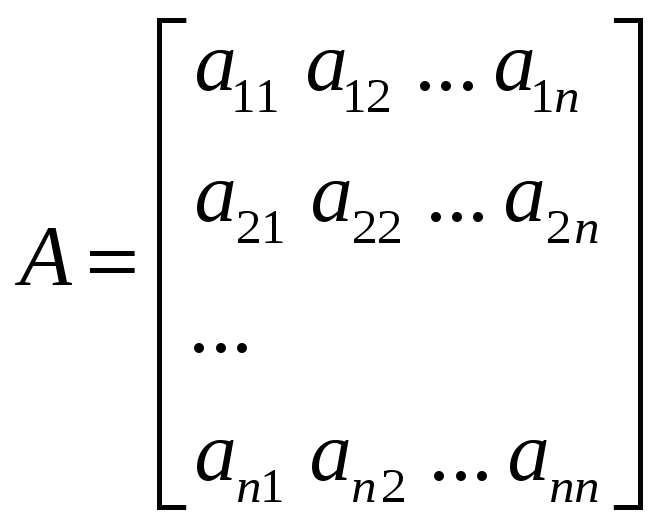 -
матрица
объекта,
размерность [n×n],
n – порядок системы.
-
матрица
объекта,
размерность [n×n],
n – порядок системы.
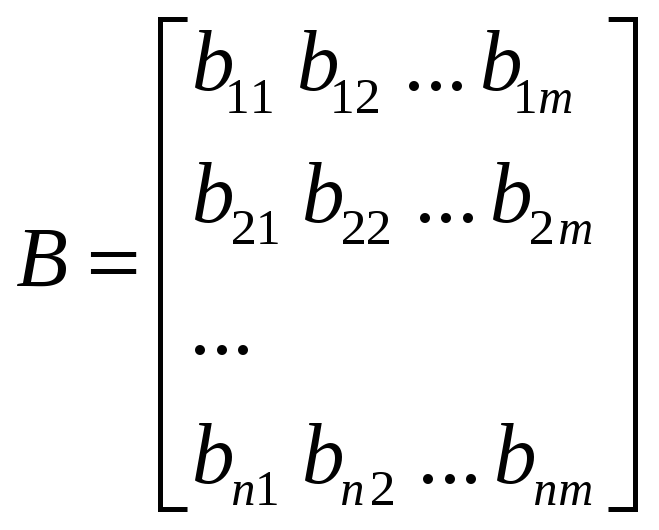 -
матрица
управления,
размерность [n×m].
-
матрица
управления,
размерность [n×m].
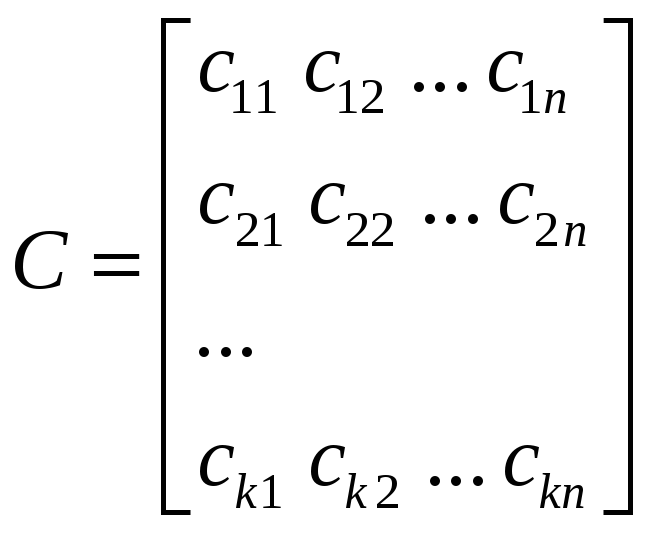 -
матрица
измерений (наблюдений),
размерность [k×n],
k
– количество входных сигналов.
-
матрица
измерений (наблюдений),
размерность [k×n],
k
– количество входных сигналов.
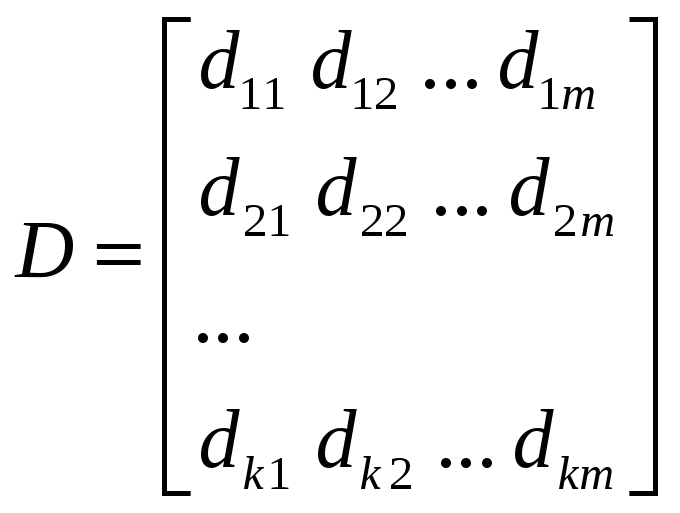 -
матрица
влияния входных сигналов на выходные,
размерность [k×m].
-
матрица
влияния входных сигналов на выходные,
размерность [k×m].
Знаменатель передаточной функции – есть характеристический полином системы. Характеристический полином системы – это уравнение, которое описывает свободной движение системы. Свободное движение системы – это движение при отсутствии внешних воздействий.
Переходная функция – это реакция системы на единичную ступенчатую функцию вида:
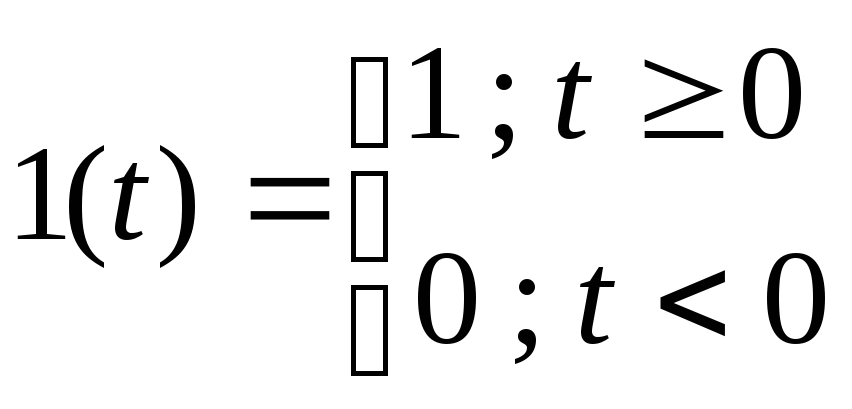
Весовая функция – это реакция системы на импульсную функцию Дирака вида:

Следствия из свойств дельта функции:
1.
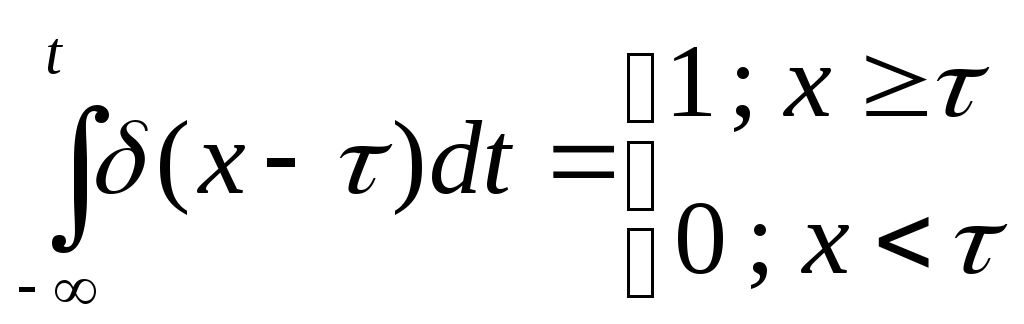
2.
![]()
Частотно-передаточной функцией от данного входа к данному выходу или комплексным коэффициентом передачи называется отношение изображения по Фурье выходной переменной к изображению по Фурье входной переменной при нулевых начальных условия и равенстве нулю прочих входов.
Частотно-передаточная функция представляет собой комплексное число, модуль которого равен отношению амплитуды выходного сигнала к амплитуде входного сигнала , а аргумент представляет собой сдвиг по фазе между выходом и входными сигналами.
Амплитудно-фазовая
частотная характеристика (АФЧХ)
– это годограф вектора частотно-передаточной
функции при изменении частоты w
от -![]() до +
до +![]()
Сопрягающая частота- это частота обратно пропорциональная постоянной времени звена
Устойчивость – способность системы возвращаться с некоторой степенью точности в исходное состояние после снятие внешних воздействий, выведших ее из этого состояния.
Определение устойчивости по Ляпунову:
Положение
равновесия xe
невозмущенной системы называется
устойчивым по Ляпунову, если для любой
положительной, сколь угодно малой
![]() окрестности существует
окрестности существует
![]() окрестность
окрестность
![]() такая, что для любого возмущения из
такая, что для любого возмущения из
![]() окрестности
окрестности
![]() справедливо выполнение условия
справедливо выполнение условия
![]()
![]() -
норма вектора
-
норма вектора
Положение
равновесия xe
невозмущенной
системы
называют асимптотически
устойчивым,
если во 1 оно устойчиво по Ляпунову, а
во 2 всякое возмущенное движение начатое
из
![]() окрестности стремиться к положению
равновесия
окрестности стремиться к положению
равновесия
![]()
Определение асимптотической устойчивости более строгое, чем устойчивость по Ляпунову.
Для того чтобы система была устойчива НЕОБХОДИМО И ДОСТАТОЧНО, чтобы ВСЕ корни характеристического полинома имели отрицательные вещественные части. Наличие ХОТЯ БЫ ОДНОГО корня с положительной вещественной частью приведет к неустойчивости всей системы в целом.
Необходимым, но недостаточным условием устойчивости линейных систем автоматического управления (САУ), является положительность ВСЕХ коэффициентов характеристического полинома (х.п.). Если хотя бы 1 коэффициент отрицателен – система неустойчива.
Критерий Гурвица.
Для того, чтобы линейная САУ была асимптотически устойчивой необходимо и достаточно, чтобы все определители Гурвица были положительны, если ao>0 или отрицательны, если ao<0.
Критерий Михайлова.
Для
того, чтобы система
была устойчивой необходимо и достаточно,
чтобы вектор годографа Михайлова D(jw)
при изменении w
от 0 до +![]() перевернулся против часовой стрелки
вокруг начала координат, нигде не
обращаясь в 0, на угол
перевернулся против часовой стрелки
вокруг начала координат, нигде не
обращаясь в 0, на угол
![]() ,
где
n
– порядок системы.
,
где
n
– порядок системы.
Для устойчивости системы необходимо и достаточно, чтобы корни вещественной и мнимой функции Михайлова чередовались, причем первый нулевой корень являлся корнем мнимой функции Михайлова.
Особенности критерия Найквиста:
Данный критерий позволяет судить об устойчивости замкнутой системы по частотным характеристикам разомкнутой системы.
Порядок х.п. замкнутой и разомкнутой систем равен n.
Если
разомкнутая
система устойчива, то для устойчивости
замкнутой системы необходимо и достаточно,
чтобы при изменении w
от -![]() до +
до +![]() АФЧХ разомкнутой системы не охватывала
точку на вещественной оси с координатами
(-1; j0).
АФЧХ разомкнутой системы не охватывала
точку на вещественной оси с координатами
(-1; j0).
Если разомкнутая система находиться на границе устойчивости, то для устойчивости разомкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы, дополненная на частоте w=0 окружностью бесконечно большого радиуса в направлении по часовой стрелке не охватывала точку на вещественной оси (-1;j0)
Если
разомкнутая
система неустойчива, то для устойчивости
замкнутой системы необходимо и достаточно,
чтобы разница между числом положительных
переходов осуществляемых АФЧХ разомкнутой
системы при изменении частоты w
от
0 до +![]() ,
через участок отрицательной вещественной
оси от -
,
через участок отрицательной вещественной
оси от -![]() до -1, и числом отрицательных переходов,
составляла величину
до -1, и числом отрицательных переходов,
составляла величину
![]() ,
где l-
число правых корней характеристического
полинома разомкнутой системы.
,
где l-
число правых корней характеристического
полинома разомкнутой системы.
Если
разомкнутая
система
неустойчива,
то для устойчивости замкнутой системы
необходимо и достаточно,
чтобы разница между числом положительных
переходов ЛФХ разомкнутой системы через
уровни ±![]() (2i+1),
совершаемых в области положительной
ЛАХ, и числом отрицательных переходов
составляет величину
(2i+1),
совершаемых в области положительной
ЛАХ, и числом отрицательных переходов
составляет величину
![]() ,
где l
-
число правых корней характеристического
полинома разомкнутой системы.
,
где l
-
число правых корней характеристического
полинома разомкнутой системы.
Порядок астатизма
Системой с астатизмом нулевого порядка или статической системой называется такая система, вынужденная установившаяся ошибка которой, при подаче на ее вход постоянного внешнего сигнала вида U(t)-U0=const постоянна и пропорциональна уровню входного сигнала.
еуст.=С0•U0=const
Системой с астатизмом первого порядка или астатической системой, называется такая система, вынужденная установившаяся ошибка которой, при подаче на ее вход линейно возрастающего сигнала U(t)=U0+Vt (U0=const,V=const) с постоянной скоростью, постоянна и пропорциональна скорости входного сигнала.
еуст.=С1•V; C0=0
Системой с астатизмом k-того порядка называется такая система, вынужденная установившаяся ошибка которой, при подаче на вход системы сигнала вида U(t)=U0+V1t +(V2/2)•t2+…+(Vk/2)•tk, где U0=const, Vi=const, 1,…,k, постоянна и пропорциональна Vk
еуст.=Сk•Vk; C0=0, C1=0,…, Ck-1=0
Порядок астатизма равен первому отличному от нуля коэффициенту в разложении ошибки.
Повышая порядок астатизма в системе, мы повышаем точность системы. Но при этом понижается запас устойчивости по фазе, т.к. за счет интегрирующего звена результирующая ЛФХ разомкнутой системы опускается на π/2.
Порядок астатизма можно увеличить путем введения интегрирующего звена в передаточную функцию разомкнутой системы.
