
- •Краткий курс сопротивления материалов
- •Часть 1
- •Глава 1. Введение
- •1.1. Задачи и методы сопротивления материалов
- •1.2. Реальный объект и расчётная схема
- •1.2.1. Модели материала
- •1.3. Классификация сил (модели нагружения)
- •1.4. Напряжения
- •1.5. Общие принципы расчёта на прочность
- •Глава 2. Центральное растяжение – сжатие прямого бруса
- •2.1. Усилия и напряжения в поперечном сечении бруса
- •2.2. Условие прочности
- •2.3. Деформации. Закон Гука
- •2.4. Расчёт стержня с учетом собственного веса
- •2.5. Статически неопределимые системы
- •2.5.1. Расчёт на действие нагрузки
- •2.5.2. Температурные напряжения
- •2.5.3. Монтажные напряжения
- •2.6. Механические характеристики материалов
- •2.6.1. Испытание на растяжение малоуглеродистой (мягкой) стали
- •Характеристики прочности
- •Характеристики пластичности
- •Разгрузка и повторное нагружение
- •Диаграммы напряжений
- •2.6.2. Испытание на сжатие различных материалов
- •2.6.3. Определение твёрдости
- •2.6.4. Сравнение свойств различных материалов
- •2.7. Допускаемые напряжения
- •2.8. Потенциальная энергия упругой деформации
- •Глава 3. Напряжённое и деформированное
- •3.1. Компоненты напряжений. Виды напряжённых состояний
- •3.2. Линейное напряжённое состояние
- •3.3. Плоское напряжённое состояние
- •3.3.1. Прямая задача
- •3.3.2. Обратная задача
- •3.4. Объёмное напряжённое состояние. Общие понятия
- •3.5.Деформации при объёмном напряжённом состоянии.
- •3.5.1. Обобщённый закон Гука
- •3.5.2. Относительная объёмная деформация
- •3.6. Потенциальная энергия упругой деформации
- •3.7. Теории прочности
- •3.7.1. Задачи теорий прочности
- •3.7.2. Классические теории прочности
- •3.7.3. Понятие о новых теориях прочности
- •Глава 4. Геометрические характеристики плоских сечений
- •4.1. Статические моменты.
- •4.2. Моменты инерции
- •4.3. Зависимость между моментами инерции при параллельном переносе осей
- •4.4. Зависимость между моментами инерции при повороте осей
- •4.5. Главные оси и главные моменты инерции
- •Глава 5. Плоский изгиб прямого бруса
- •5.1. Конструкция опор. Определение реакций. Внутренние усилия
- •5.2. Дифференциальные и интегральные зависимости между q, q и m
- •5.3. Построение эпюр поперечной силы q и изгибающего момента m
- •5.4. Нормальные напряжения при чистом изгибе
- •5.5. Условие прочности по нормальным напряжениям. Рациональные формы сечений
- •5.6. Касательные напряжения при поперечном изгибе
- •5.7. Распределение касательных напряжений в балках
- •5.8. Напряжённое состояние при поперечном изгибе.
- •5.9. Касательные напряжения в полках тонкостенных профилей. Центр изгиба
- •Нормальные напряжения:
- •5.10. Потенциальная энергия упругой деформации
- •Глава 6. Сдвиг
- •6.2. Проверка прочности и допускаемые напряжения при чистом сдвиге
- •6.3. Расчёт заклёпочных и сварных соединений
- •Глава 7. Кручение прямого бруса
- •7.1. Основные понятия. Определение крутящих моментов
- •7.2. Напряжения и деформации при кручении стержней круглого и кольцевого сечений
- •7.3. Расчёт валов на прочность и жёсткость
- •7.4. Разрушение валов из различных материалов. Потенциальная энергия упругой деформации
- •7.5. Кручение стержней прямоугольного сечения
- •7.6. Расчёт цилиндрических винтовых пружин с малым шагом
- •Оглавление
3.2. Линейное напряжённое состояние
Линейное напряжённое состояние имеет место в стержнях, испытывающих растяжение или сжатие, а также в некоторых точках стержня, работающего на изгиб. Рассмотрим растяжение стержня. Как указывалось в главе 2, в поперечных сечениях, удалённых от точек приложения внешних сил, нормальные напряжения распределены равномерно и равны (рис.3.5,а)
![]() . (3.3)
. (3.3)
Эти напряжения являются главными, т.к. касательные напряжения в поперечном сечении равны нулю. Напряжённое состояние при растяжении является однородным, поэтому размеры выделяемых элементов не играют никакой роли. Определим напряжения, действующие по наклонной площадке. Наклон площадки определяется острым углом α между направлением оси стержня и нормалью nα к площадке. Условимся считать угол α положительным, если он отсчитывается против часовой стрелки (рис.3.5,а). Элемент, находящийся в линейном напряжённом состоянии, изображаем в виде плоской фигуры, помня, однако, что в действительности он имеет вид, показанный на рис.3.4,а.
Рассмотрим равновесие нижней части стержня, отсечённой наклонной площадкой (рис.3.5,б). По наклонной площадке, площадь которой равна Fα, равномерно распределены напряжения pα, параллельные осевой силе N = P, следовательно, результирующая этих напряжений
pαFα = N.
Отсюда найдём pα,
подсчитав предварительно
![]() ,
,
![]() .
.
Проектируя pα на нормаль nα и на плоскость сечения, получим выражения для нормальных и касательных напряжений по наклонной площадке:
σα = pαcos α, τα = pαsin α
или
σα = σ1cos2α. (3.4)
![]() . (3.5)
. (3.5)
а б в

Рис.3.5
Как видно из формул (3.4) и (3.5), при α = 0 τα = 0 и σα = σ1, при α = π/2 σα = 0 и τα = 0. Таким образом, при растяжении действительно имеет место линейное напряжённое состояние: σ1 = N/F, σ2 = σ3 = 0. При сжатии σ3 = – N/F, σ1 = σ2 = 0.
Из выражения (3.5) видно, что касательные напряжения достигают своей наибольшей величины при α = ± 450, причём
![]() . (3.6)
. (3.6)
Определим теперь напряжения, действующие по площадке, перпендикулярной заданной наклонной, α1 = α + 900 (рис.3.5,в):
σα1 = σ1 ∙ cos2 (α + 90) = σ1sin2 α,
![]() .
.
Итак
σα+90 = σ1sin2 α. (3.7)
![]() . (3.8)
. (3.8)
3.3. Плоское напряжённое состояние
Плоское напряжённое состояние встречается в деталях машин и в строительных конструкциях очень часто. Например, это стержень при кручении (рис.3.6,а) и изгибе (рис.3.6,б), тонкостенный сосуд под действием внутреннего давления (рис.3.6,в).
а б в

Рис.3.6
Плоское напряжённое состояние также имеет место в тонкой пластине, нагруженной силами, параллельными её плоскости и равномерно распределёнными по толщине (рис.3.7): σх ≠ 0, σу ≠ 0, τху ≠ 0, σz = τzx = τzy = 0.
Рассмотрим два аспекта задачи о плоском напряжённом состоянии: найдём напряжения, действующие по наклонной площадке (прямая задача), и найдём величины и направления главных напряжений (обратная задача).

Рис.3.7
3.3.1. Прямая задача
Дано: напряжения σх, σу, τху, угол α > 0 (рис.3.8,а).
Определить: напряжения σα и τα (рис.3.8,б).
Рассмотрим равновесие элемента abc. При записи уравнений статики будем определять силу как произведение напряжения на площадь соответствующей грани:
площадь наклонной грани bc = dF;
площадь прямой грани ab = dF ∙ cos α;
площадь прямой грани ac = dF ∙ sin α.
а б в

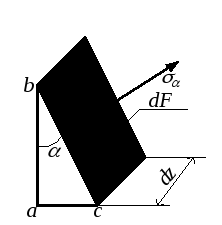
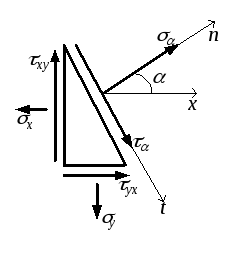
Рис.3.8
Теперь запишем уравнения проекций всех сил, действующих на элемент abc, на нормаль к наклонной площадке и на ось, совпадающую с этой площадкой (рис.3.8,в).
∑n = 0: σαdF – σx dF cos α ∙ cos α – σу dF sin α ∙ sin α + τxу dF cos α ∙ sin α + τух dF sin α ∙ cos α = 0,
∑t = 0: ταdF + σу dF sin α ∙ cos α + τуx dF sin α ∙ sin α – τxу dF cos α ∙ cos α – σх dF cos α ∙ sin α = 0.
После несложных преобразований и сокращения на dF получаем следующие выражения:
σα = σх cos2α + σy sin2α – τxy sin 2α , (3.9)
![]() . (3.10)
. (3.10)
|
Рис.3.9 |
Если исходные площадки являются главными (рис.3.9), то формулы (3.9) и (3.10) упрощаются: σα = σ1cos2α + σ2sin2, (3.11)
Из формулы (3.12) следует, что наибольшее касательное напряжение |
действует по площадке, наклонённой под углом 450 к главным площадкам:
![]() . (3.13)
. (3.13)
Преобразуем формулу (3.9), используя выражение для тригонометрических функций
![]() и
и
![]() .
.
Получим
![]() . (3.14)
. (3.14)
Теперь определим напряжения, действующие по площадке, перпендикулярной к заданной: α1 = α + 900. Воспользуемся формулой (3.14), учитывая, что cos 2α1 = – cos 2α и sin 2α1 = – sin 2α. Получим
![]() . (3.15)
. (3.15)
Сложим (3.14) и (3.15), чтобы найти сумму нормальных напряжений, действующих по взаимно перпендикулярным площадкам.
Получим
σα + σα + 90 = σх + σу = const, (3.16)
т.е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам инвариантна по отношению к наклону этих площадок.

