Методика составления формул для определения передаточного отношения планетарной передачи
Определим передаточное отношение iah от колеса a к водилу h в планетарной передаче с неподвижным колесом в (рис.14). Оно представляет собой отношение угловых скоростей колеса а и водила: iah = ωa / ω в .
Подготавливаем выражение для нахождения iah в зависимости от передаточного отношения при неподвижном водиле, для чего применяем формулу Виллиса. Для удобства практического применения формулы освобождаемся от знаменателя:
Применительно к нашей расчётной схеме полагаем ωв =0. Уравнение упрощается. Определяется
(13)
Для того чтобы
определить передаточное отношение
при неподвижном водиле в зависимости
от чисел зубьев зубчатых колёс, выполняем
обращение движения и вычерчиваем
кинематическую схему механизма,
полученного после обращения движения
(рис. 15).
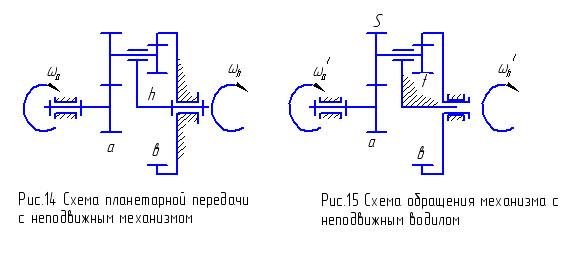
Этот механизм представляет собой двухступенчатую передачу с неподвижными осями зубчатых колёс, в которой
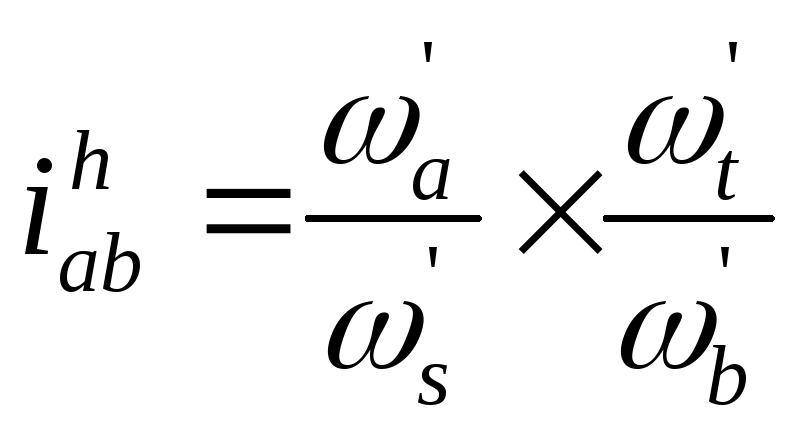, (14)
где ωs’ и ωt’ - угловые скорости сателлитов, ωs’ = ωt’ .
Заменяем отношения угловых скоростей обратными отношениями чисел зубьев с учётом знаков передаточных отношений:
. (15)
Путём подстановки выражения (15) в равенство (13) получаем формулу для определения передаточного отношения в планетарной передаче в зависимости от чисел зубьев зубчатых колёс:
.
Пусть, например, Za =16, Zs=48, Zt =16, Zb=80.
Тогда
=
16
.
Передаточное отношение имеет знак «плюс». Следовательно, ведомое звено (в данном случае – водило) вращается в ту же сторону, что и ведущее звено (колесо а ).
Порядок выполнения работы
1. Составьте и вычертите кинематическую схему заданной планетарной передачи. Обозначьте зубчатые колеса и водило. Укажите ведущее звено. Определите числа зубьев зубчатых колёс.
2. Составьте формулу передаточного отношения планетарной передачи в зависимости от передаточного отношения при неподвижном водиле при помощи формулы Виллиса.
3. Вычертите кинематическую схему многоступенчатой передачи, получаемой после обращения движения, и определите передаточное отношение при неподвижном водиле в зависимости от чисел зубьев зубчатых колёс.
4. Составьте формулу для определения передаточного отношения планетарной передачи в зависимости от чисел зубьев зубчатых колёс и выполните числовой расчёт.
Если лабораторная работа выполнилась по модели механизма, определите передаточное отношение, сосчитав число оборотов ведущего звена за один оборот ведомого. Сопоставьте результаты.
Содержание отчёта
В отчёте следует отразить все этапы выполнения лабораторной работы. Отчёт должен содержать:
1. Схему планетарной передачи.
2. Параметры зубчатых колёс.
3. Вывод расчётной формулы и вычисление передаточного отношения.
4. Результаты замера передаточного отношения экспериментальным путём.
Контрольные вопросы
1. Редуктор – это зубчатый механизм, …
а) понижающий угловую скорость вращения;
б) повышающий угловую скорость вращения;
в) имеющий планетарные зубчатые колёса.
2. Мультипликатор – это зубчатый механизм, …
а) имеющий планетарные зубчатые колёса;
б) повышающий угловую скорость вращения;
в) понижающий угловую скорость вращения.
3. Цилиндрическая зубчатая передача, в которой угловые скорости вращения колес имеют разные знаки – это …
а) внешнее зацепление;
б) внутреннее зацепление;
в) реечное зацепление;
4. Цилиндрическая зубчатая передача, в которой угловые скорости вращения колес имеют одинаковые знаки – это …
а) внешнее зацепление;
б) реечное зацепление;
в) внутреннее зацепление.
5. Передаточное отношение зубчатой пары определяется по зависимости …
а)
; б)
; в)
.
6. Передаточное отношение многоступенчатой передачи равно … передаточных отношений всех её ступеней.
а) сумме ; б) произведению ; в) разности .
7. Планетарная зубчатая передача отличается от обычной многоступенчатой тем, что …
а) обязательно используются колёса с внутренним зацеплением ;
б) имеются соосные колёса ;
в) имеются колёса, оси которых вращаются в пространстве .
8. Планетарный редуктор (с одной степенью свободы) можно получить из дифференциального механизма (с двумя степенями свободы), если …
а) сделать неподвижным водило ;
б) сделать неподвижным планетарное колесо ;
в) сделать неподвижным одно из центральных колёс.