Кинематический расчёт многоступенчатой передачи с неподвижными осями зубчатых колёс

Кинематический расчёт многоступенчатой передачи является составной частью кинематического расчёта планетарного механизма. В связи с этим необходимо предварительно усвоить методику этого расчета.

Многоступенчатая передача с неподвижными осями зубчатых колёс состоит из ряда зубчатых пар, связанных в единую кинематическую цепь. Каждую зубчатую пару называют ступенью передачи. Задача кинематического расчёта многоступенчатой передачи состоит в том, чтобы определить передаточное отношение от ведущего вала к ведомому и направление вращения ведомого вала по заданному направлению вращения ведущего.

Пусть требуется выполнить кинематический расчёт четырёхступенчатой передачи (рис. 12). Ведущим валом, получающим движение от двигателя, служит вал с зубчатым колесом Z₁. Зубчатое колесо Z₁, связанное с последним ведомым валом, имеет в нашем примере внутренний зубчатый венец и образуется с колесом Z₆ зубчатую пару внутреннего зацепления. Зубчатое колесо Z₆ участвует в двух зубчатых парах. Известны числа зубьев зубчатых колёс.

Определяем передаточное отношение i₁₇ = ω₁/ω₇ (где ω₁ и ω₇ - угловая скорость ведущего и ведомого валов), а также знак передаточного отношения.

Для того чтобы вывести формулу для определения передаточного отношения многоступенчатой передачи, его разбивают на сомножители по числу ступеней и заменяют отношения угловых скоростей зубчатых колёс на каждой ступени соответствующими обратными отношениями чисел зубьев с учётом знака передаточного отношения на каждой ступени.

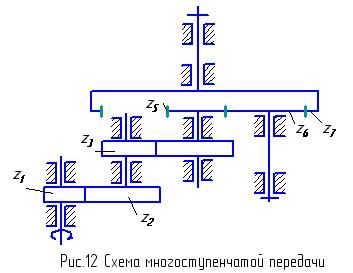
Передаточному отношению тех ступеней, где применяется внешнее зацепление, приписывается знак “минус” (так как при этом изменяется направление вращения ведомого вала), в случае внутреннего зацепления – знак “плюс”.

Для схемы, предоставленной на рис.11, передаточное отношение разбивается на четыре сомножителя:

Отношения угловых скоростей заменяются обратными отношениями чисел зубьев с учётом знаков передаточного отношения:

Здесь Z₁ - Z₇ - числа зубьев зубчатых колёс. После подстановок получаем:

ֹ

Передаточное отношение рассматриваемой четырёхступенчатой передачи имеет знак «минус», следовательно, ведущий и ведомый валы вращаются в разные стороны. Зубчатое колесо Z₆ не повлияло на числовое значение передаточное отношение, но изменило его знак. Такие зубчатые колёса называют паразитными колёсами. Их применяют для изменения направления вращения и для передачи движения между далеко отстоящими валами.

Метод обращения движения и формула Виллиса

Угловые скорости центральных зубчатых колёс и водило связаны в планетарных механизмах уравнением, которое называют формулой Виллиса. При составлении формулы применяется общее направление отсчёта положительных угловых скоростей основных звеньев, одинаковое для всех звеньев (рис.13, а).

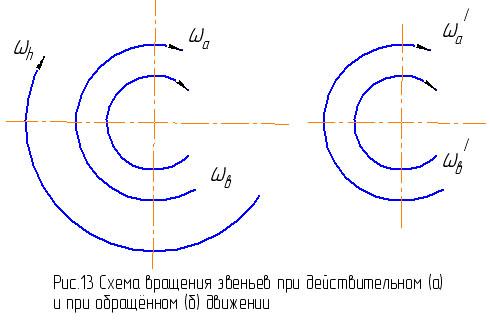
Если всем основным звеньям планетарного механизма сообщить дополнительное вращательное движение около их общей оси в направлении, противоположном направлению отсчёта угловых скоростей, с угловой скоростью, равной скорости водила, то водило станет неподвижным (рис.13, б), а угловые скорости ω_a^’ и ω_в^’ центральных зубчатых колёс будут определяться по формулам:

ω_a^’ = ω_a - ω_{h ,} ω_в^’ = ω _в - ω_h .

После обращения движения и остановки водила механизм представляет собой многоступенчатую передачу с неподвижными осями зубчатых колёс. В этой передачи передаточное отношение от колеса а колесу в будет определяться по формуле: = ω_a^’ / ω_в^’ . Подставляя ω_a^’ и ω_в^’ , получаем формулу Виллиса:

Здесь - передаточное отношение от колеса a к колесу b при неподвижном водиле, определяемое в зависимости от чисел зубьев зубчатых колёс.

Формулу Виллиса можно применять ко всем планетарным механизмам. В случае, если рассматривается механизм с одной степенью свободы, угловую скорость закреплённого центрального колеса полагают в формуле Виллиса равной нулю. Из полученного упростившегося уравнения можно вычислить требующееся передаточное отношение планетарной передачи в зависимости от передаточного отношения при неподвижном водиле.

Затем анализируется передача с неподвижными осями зубчатых колёс, полученная в результате обращения движения, и определяется передаточное отношение при неподвижном водиле в зависимости от чисел зубьев зубчатых колёс.