Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Санкт-Петербургский институт машиностроения (ВТУЗ-ЛМЗ)

Кафедра теории механизмов и деталей машин

ПРОФИЛИРОВАНИЕ ЭВОЛЬВЕНТНЫХ ЗУБЬЕВ

МЕТОДОМ ОГИБАНИЯ.

КИНЕМАТИЧЕСКИЙ РАСЧЁТ ПЛАНЕТАРНЫХ ПЕРЕДАЧ

Методические указания

к выполнению лабораторных работ

Санкт-Петербург

2008

Профилирование эвольвентных зубьев методом огибания. Кинематический расчёт планетарных передач: методические указания по выполнению лабораторных работ для студентов всех специальностей.

Изложены общие теоретический сведения для самостоятельной проработке по соответствующим разделам курса “Теория механизмов и машин”. Дано описание лабораторной установки, указываются порядок выполнения работы и содержание отчёта.

Составитель: канд. техн. наук, доц. В.А. Трубняков

Методические указания утверждены на заседании кафедры

Рецензенты: канд. техн. наук, доц. А.А.Янсон

Редактор Г.Л. Чубарова

П 21 (03)

Подписано в печать Формат 60x90 1/16

Бумага тип. № 3. Печать офсетная. Усл. печ. л.

Уч.-изд.л. Тираж 100 экз. Заказ №

Издание Санкт – Петербургского института машиностроения

195197, Санкт – Петербург, Полюстровский пр., 14.

ОП ПИМаш

Лабораторная работа №1

ПРОФИЛИРОВАНИЕ ЭВОЛЬВЕНТНЫХ ЗУБЬЕВ

МЕТОДОМ ОГИБАНИЯ

Цель работы – усвоение методики геометрического расчёта цилиндрического эвольвентного колеса.

Общие сведения

Метод огибания. В настоящее время большинство зубчатых колес нарезаются высокопроизводительным методом огибания. Суть его заключается в том, что на станке за счет согласованных движений инструмента и заготовки воспроизводится зацепление зубьев инструмента (чаще реечного типа) и нарезаемого колеса. При этом профиль зуба колеса получается как огибающая семейства профилей инструмента, образуемого в относительном движении. Наибольшее распространение в машиностроении получили зубчатые колеса с эвольвентным профилем, который получается методом огибания при прямолинейном профиле инструмента реечного типа.

Исходный контур. Формы и размеры зубьев колес, нарезаемых методом огибания, зависят от профиля применяемого при этом инструмента реечного типа. Реечный профиль называется исходным контуром. Параметры исходного контура для цилиндрических эвольвентных колес (рис.1) стандартизованы (ГОСТ 13755-81). Профиль зуба прямолинейный и сопрягается с линией впадин дугой окружности. Стандартом установлены следующие параметры и коэффициенты исходного контура:

угол профиля ⁰;

коэффициент высоты головки зуба h= 1;

коэффициент радиального зазора с^*= 0,25;

коэффициент радиуса кривизны переходной кривой = 0,38.

Абсолютные размеры исходного контура получают умножением соответствующего коэффициента на модуль m:

высота головки зуба h_аo=hm;

высота ножки зуба h_fo=(h+ c^*)m;

радиальный зазор с=с^*m;

радиус скругления во впадине =m;

шаг р= m; (1)

толщина зуба по делительной прямой s₀ = 0,5p = 0,5m;

ширина впадины по делительной прямой е_о = 0,5р = 0,5m.

Значение модулей (в мм) устанавливает ГОСТ 9563-60.

Производящий исходный контур, используемый для профилирования инструмента, имеет дополнительную часть (заштрихованную на рис.1).

Элементы зубчатого колеса. Базой для определения элементов зубьев и их размеров принята окружность радиуса r, которая называется делительной (рис.2).

Размеры зуба определяются толщиной зуба s по делительной окружности, а также высотой головки h_а и высотой ножки h_f, которые измеряются как расстояния от делительной окружности соответственно до окружности вершин радиуса r_a и окружности впадин радиуса r_f. Расстояние между зубьями определяется шириной впадины е или шагом р по делительной окружности, который равен шагу на исходном контуре (1).

Перечисленные размеры связаны очевидными соотношениями

r_a = r+h_a,, r_f = r-h_f, p=s+e.

Количество шагов, размещающихся на длине делительной окружности, равно числу зубьев z:

2r=zp,

откуда радиус делительной окружности, с учетом (1),

r = 0,5mz. (2)

Угол профиля в точке А на делительной окружности равен углу профиля исходного контура .

Главный профиль очерчен по эвольвенте основной окружности радиуса r_b. По свойству эвольвенты касательная AN к основной окружности является нормалью к эвольвенте. ПоэтомуAON = , как углы с параллельными сторонами (касательная AN перпендикулярна радиусу ON). Тогда из прямоугольного AON следует

r_b=rcos. (3)

Станочное зацепление. При нарезании зубчатого колеса инструментом реечного типа на станке воспроизводится реечное зацепление нарезаемого колеса с исходным контуром, которое называется станочным (рис.3). Начальная окружность колеса совпадает с делительной. Начальная прямая рейки I касается делительной окружности колеса в полюсе Р. Делительная прямая рейки 2 в общем случае не совпадает с начальной и ее положение определяется смещением xm, где m- модуль, х – коэффициент смещения. Показанное на рис.3 смещение считается положительным. Если делительная прямая рейки пересекает делительную окружность колеса, то х < 0. В частном случае, когда делительная и начальная прямые рейки совпадают, то х = 0.

Движения рейки и колеса согласовываются в соответствии с зависимостью

V_o= r,

где V₀ - cкорость поступательного движения рейки, - угловая скорость вращения колеса.

Точка касания К профиля зуба колеса с исходным контуром лежит на общей нормали к ним, проходящей через полюс. Эта нормаль КN совпадает с касательной к основной окружности и является линией зацепления, представляющей собой геометрическое место точек касания профиля зуба колеса с исходным контуром. По построению, угол PON равен углу профиля исходного контура .

Размеры зуба колеса определяются параметрами исходного контура и его расположением относительно нарезаемого колеса. Толщина зуба колеса s по делительной окружности равна ширине впадины e_wo рейки по начальной прямой.

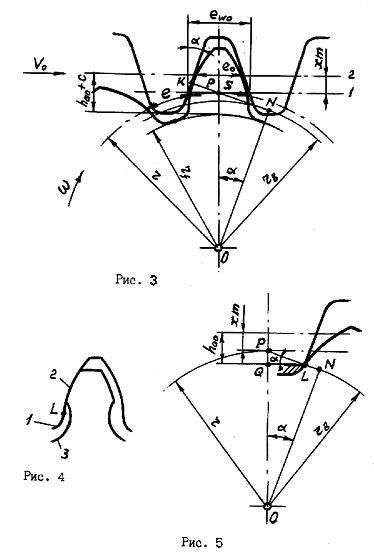
Из рис. 3

s = e_wo= e_o+2xmtg,

или

s = m(0,5+2xtg). (4)

Ширина впадины по делительной окружности

e = p - s = m(0,5-2xtg. (5)

Радиусы окружностей впадин и вершин.

r_f = m(0,5z - h- c^*+ x). (6)

r_а = m(0,5z+ x+ h)

Следует отметить, что радиус окружности вершин определяется по приведённой формуле только при реечном зацеплении.

Подрезание зубьев. Обычно переходная кривая I (рис.4), формируемая скругленной вершиной исходного контура, плавно сопрягается в точке L с главным эвольвентным профилем 2, образуемым прямолинейным участком исходного контура. Однако, в некоторых случаях переходная кривая 3 пересекает главный профиль. Такое явление называется подрезанием зуба. Подрезание уменьшает эвольвентную часть профиля зуба и его толщину у основания, что отрицательно сказывается на работоспособности колеса.

Для выявления условия отсутствия подрезания рассмотрим станочное зацепление в положении, когда формируется точка сопряжения L. При этом граница прямолинейного участка исходного контура располагается на линии зацепления (рис.5).

Подрезание отсутствует, если граница активного участка линии зацепления L лежит в пределах теоретической линии зацепления PN. Таким образом, условие отсутствия подрезания можно выразить неравенством

PLPN.

Угол PLQ равен , так как его стороны перпендикулярны сторонам угла PON. Тогда изPLQ

PL = (h_ao - xm)/sin,

а из PON PN = r ∙sin.

После подстановки этих выражений в исходное неравенство и выполнения преобразований получим 2(h-x)zsin² .

Из этого условия можно получить формулу для определения минимального числа зубьев колеса, при котором отсутствует подрезание

z_min=2(h-x)/sin² .

При х=0 имеем

z_{min o} =2h/sin² . (7)

Стандартному исходному контуру соответствует

z_{min o}=17.

Из того же условия можно получить формулу для определения минимального коэффициента смещения, при котором отсутствует подрезание

x_min= h- 0,5zsin ² ,

или с учетом формулы (7)

x_min=h(z_{min o} - z)/z_{min o}. (8)

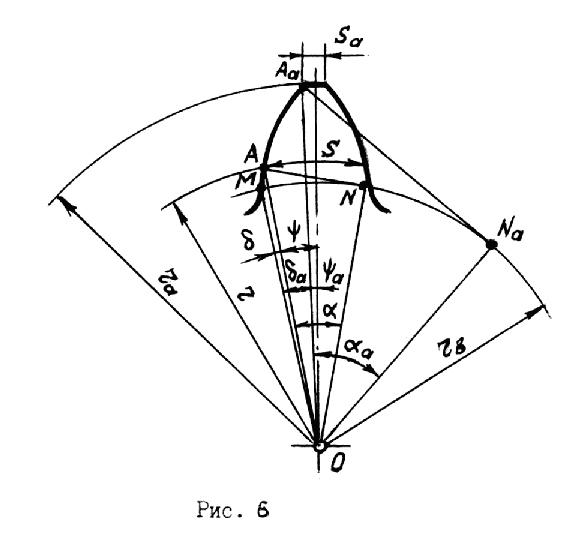
Заострение зубьев. Положительное смещение, применяемое для устранения подрезания при малом числе зубьев колеса, приводит к уменьшению толщины зуба на окружности вершин s_a. Если это уменьшение происходит ниже некоторого предела, снижается прочность вершинной части зуба. Такое явление называется заострением. На практике принимают

s_a 0,2m.

Для определения величины s_a рассмотрим рис.6. Точки М, А, A_a эвольвентного профиля, лежащие соответственно на окружностях основной, делительной и вершин, соединим с центром колеса О. Кроме того, из них проведены касательные AN и A_aN_a к основной окружности и точки касания также соединены с центром. При этом образуются следующие углы : половина угловой толщины зуба и на окружностях делительной и вершин, эвольвентный угол и в точках А и A_a, угол профиля и в точках A и A_a.

Исходя из принципа образования эвольвенты, длина касательной к основной окружности равна длине соответствующей дуги этой окружности AN = MN,

или r_btg = r_b(.

Отсюда

Аналогично = tg -= inv

Непосредственно из рис.6 следует

+.

Учитывая, что s = 2r, s_a = 2r_a_а ,

после преобразований получим

s_a = r_a (9)

Угол определяется из

(10)

Описание лабораторной установки

Схема установки изображена на рис.7. На основании 1 установлены диск 2 и рейка 3. Вращение диска и поступательное перемещение рейки связаны между собой: окружные скорости точек диска на его делительном цилиндре d совпадают со скоростью поступательного движения рейки. Совместное движение рейки и диска осуществляется при помощи шагового храпового механизма, приводящегося в действие от рычага 4. Рейка имеет также возможность поперечного перемещения. Благодаря этому её можно установить так, что по делительной окружности диска будет катиться по ней без скольжения любая начальная прямая рейки. Установка положения рейки осуществляется по шкале 5.

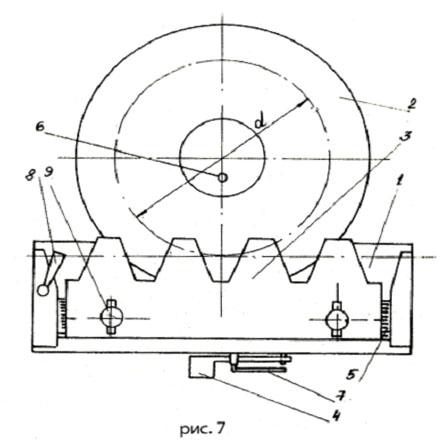
На верхней плоскости рейки приводится основные данные прибора: m – модуль, мм ; α – угол профиля рейки; d – диаметр делительной окружности.

Порядок выполнения работы и содержание отчёта

1. Ознакомиться с прибором. Опробовать механизм передвижения рейки. Средняя линия рейки должна быть установлена против нулевых значений шкалы 5.

2. Произвести расчёты, необходимые для выполнения работы:

а) определить число зубьев вычерчиваемого (нарезаемого) колеса по формуле: Z = d/m

б) определить диаметр основной окружности

dв = d cosα ;

в) определить радиус окружности выступов колеса, нарезанного без смещения инструмента.

,

где h= 1 – коэффициент высоты головки зуба;

г) определить минимальное число зубьев, при котором отсутствует подрезание при нарезании данной рейкой прямозубого колеса (формула 7)

д) сравнить полученные величины Z и Z_min и определить необходимое смещение рейки для устранения подрезания при нарезании донного колеса

;

е) определить величину радиуса r_a окружности выступов колеса, нарезанного со смещением.

3. С помощью приспособления вырезать из плотной бумаги круг диаметра, указанного на диске прибора. На круге провести циркулем следующем окружности:

а) основную диаметра dв;

б) окружность выступов нулевого колеса радиуса ( на одной половине круга);

в) окружность выступов колеса со смещением радиуса r_a (на второй половине круга).

4. Наложить круг на три иглы диска 2 и прижать его крышкой. При нарезании без смещения установить xm = 0. Поворотом рычага 7 влево отключить храповой механизм и отвести рейку в крайнее правое положение. Поворотом рукоятки 8 в крайнее левое положение освободить диск 2 и повернуть его таким образом, чтобы в контакт с рейкой вошла половина круга, предназначенная для вычерчивания (нарезания) некорригированного колеса. После этого вернуть рукоятку 8 в крайнее правое положение, обеспечивающее согласованное перемещение рейки и диска с кругом. Установка готова к работе.

В данном случае бумажный круг, укреплённый на диске, можно рассматривать как заготовку зубчатого колеса, закреплённую на столе зубострогального станка. Инструментом для нарезания служит рейка, поступательное движение которой связано с вращением заготовки. На станке инструментальная рейка получает возвратно-поступательное движение резания вдоль оси колеса.

5. Остро отточенным карандашом на бумажном круге прочерчивается контур зубьев рейки. Нажимом на рычаг 4 передвигают рейку (а вместе с ней поворачивается круг-заготовка) на один шаг храпового устройства и вновь очерчивают контур зубьев рейки. Так продолжают до тех пор; пока рейка не придёт в крайнее левое положение, а на бумажном круге будет получен (как огибающая семейства положений зубьев рейки) профиль двух-трёх зубьев нулевого колеса. На реальной заготовке за счёт движения резания весь материал впадин между зубьями будет выбран.

6. Повторить операции для вычерчивания (нарезания) зубьев колеса, нарезаемого со смещением, на второй половине круга. При этом рейку надо сместить от центра колеса на расчётную величину xm и зафиксировать винтами 9.

Содержание отчёта

1. Схема станочного зацепления (рис.3.)

2. Расчёты, проделанные при выполнении работы.

3. Результаты профилирования зубчатых колёс методом огибания.

Контрольные вопросы

1. Шаг зубьев по делительной окружности в цилиндрической передаче равен

а) р=m x π ; б) р=m/π ; в)р=2m x π .

2. Основная окружность эвольвентного колеса – это окружность, …

а) проходящая через основание зуба;

б) с которой образуется эвольвента профиля зуба;

в) проходящая через вершины зубьев.

3. Эвольвента образуется как след …

а) любой точки окружности, перекатываемой без скольжения по другой окружности;

б) любой точки окружности, перекатываемой без скольжения по прямой линии;

в) любой точки прямой линии, перекатываемой без скольжения по окружности.

4. Окружности цилиндрического колеса, на которой шаг зубьев р, модуль m и угол профиля α равны шагу, модулю и углу профиля исходного контура рейки, называется …

а) делительной ; б) основной ; в) начальной.

5. Размеры заготовки для зубчатого колеса определяет радиус …

а) окружности вершин зубьев;

б) начальной окружности;

в) основной окружности.

6. Радиус делительной окружности определяется по формуле …

а) r = 0.5m x Z ; б) r = πm x Z ; в) r = 2m x Z .

7. Размерность модуля m ...

а) М ; б) ММ ; в) безразмерная величина .

8. С увеличением коэффициента смещения при нарезании эвольвентных колёс опасность заострения зубьев …

а) увеличивается;

б) уменьшается;

в) смещение не влияет на заострение зубьев.

9. Подрезание зубьев при нарезании может возникнуть …

а) у основания зуба ; б) на вершине зуба ; в) в районе полюса зацепления .

10. Для избежания подрезания зубьев при нарезании необходимо …

а) перейти на другой модуль m;

б) использовать положительное смещение инструмента при нарезании;

в) увеличить твёрдость зубьев.

11. За счёт подбора коэффициентов смещения при нарезании колёс нельзя …

а) подобрать требуемое межосевое расстояние;

б) изменить передаточное отношение;

в) увеличить контактную и изгибную прочность зубьев;

г) устранить подрезание при нарезании.

12. При нулевом коэффициенте смещения инструмента (Х=0) средняя линия рейки и делительная окружность колеса …

а) касаются в полюсе ; б) не имеют общих точек ; в) пересекаются .

13. При положительном смещении инструмента (Х>0) средняя линия рейки и делительная окружность колеса …

а) касаются в полюсе ; б) не имеют общих точек ; в) пересекаются .

14. При отрицательном смещении инструмента (Х<0) средняя линия рейки и делительная окружность колеса …

а) касаются в полюсе ; б) не имеют общих точек ; в) пересекаются .

15. При нарезании прямозубого колеса по методу огибания рейкой её скорость совпадает со скоростью колеса на …

а) основной окружности;

б) делительной окружности;

в) окружности вершин.

Лабораторная работа №2

КИНЕМАТИЧЕСКИЙ РАСЧЁТ ПЛАНЕТАРНЫХ ПЕРЕДАЧ

Цель работы – усвоение методики определения передаточного отношения планетарной передачи.

При подготовки к практическому занятию необходимо усвоить разделы курса ТММ, касающиеся структуры и кинематики сложных зубчатых механизмов, а именно: кинематический расчёт плоских многоступенчатых передач с неподвижными осями вращения зубчатых колёс, разновидности плоских планетарных механизмов, метод обращения движения при кинематическом расчёте планетарных механизмов и уравнение связи угловых скоростей основных звеньев планетарного механизма (формула Виллиса).

Перечисленные теоретические вопросы составляют основу методики кинематического расчёта планетарных механизмов. Краткие справочные данные по упомянутым вопросам приводятся ниже.