Глава 9 Уравновешивание роторов

к δ1m

Значение критической угловой скорости вала можно считать как собственную частоту рассматриваемой системы. поскольку на вал действуют силы сопротивления, то при ω = ωк действительный прогиб вала х не

Из полученного выражения видно, что при ω < ωк прогиб х > 0 (дорезонансный режим). Таким образом, в зарезонансном режиме сдвиг фаз между колебаниями вынуждающей силы и собственными колебаниями равен π. С увеличением угловой скорости ω в зарезонансном режиме прогиб вала х уменьшается, а при ω → ∞ стремится к смещению rS. В зарезонансном режиме центробежная сила инерции будет равна /11/:

т.е. с увеличением угловой скорости происходит уменьшение дисбаланса. Если на валу укреплено несколько дисков, то такая колебательная система будет иметь несколько критических (резонансных) угловых скоро-

стей /11/.

Особенность балансировки такого ротора заключается в том, что плоскости коррекции не могут быть выбраны произвольно. По методическим указаниям к ГОСТ 22061-76 можно установить оптимальные плоскости коррекции. Установка корректирующих масс в оптимальных плоскостях коррекции вызывает минимальные прогибающие моменты в теле ротора и позволяет на частоте вращения ниже первой резонансной сохранить полученную уравновешенность ротора в широком диапазоне частот вращения /11/.

Согласно ГОСТ 19534-70 к «жестким» роторам относятся роторы, у которых после балансировки в двух произвольно выбранных плоскостях коррекции на частоте вращения ниже первой резонансной системы «ротор

– опоры» значение остаточных дисбалансов в плоскости опор не превзойдут допустимых значений на эксплуатационных частотах вращения. Все остальные роторы относятся к «гибким» /11/.

9.6. Станки для статической и динамической балансировки роторов

Даже полностью сбалансированный на стадии проектирования ротор после изготовления обладает некоторой неуравновешенностью. Появление неуравновешенности вызвано неоднородностью материала, отклонением фактических размеров от номинальных. Данная неуравновешенность уст-

раняется на специальных балансировочных станках /13/.

Для роторов, имеющих малые размеры вдоль оси вращения, можно ограничиться статической балансировкой. В этом случае определяется

только главный вектор дисбалансов D . Если не требуется высокая точность балансировки, то она может быть выполнена в статическом режиме, способом описанном выше (п.8.2). Существует другой, более точный способ определения статической неуравновешенности в динамическом режиме, т.е. в процессе вращения ротора /13/.

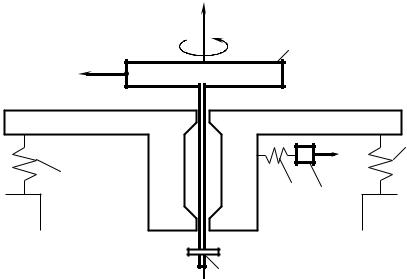
На рис. 9.9 показана схема балансировочного станка работающего по этому принципу. Ротор 1 закрепляется на шпинделе 4, который вращается с постоянной угловой скоростью относительно плиты 2. Через упругие элементы 3 плита опирается на станину. С помощью мягкой пружины 5 масса сейсмического датчика 6 связана с плитой 2. Жесткость пружины 5 выбирается таким образом, чтобы собственная частота колебаний массы датчика была значительно ниже частоты вращения ротора. Масса 6 может свободно совершать прямолинейное движение вдоль оси х, которая проходит через центр масс плиты. В процессе вращения шпинделя и ротора ось z ротора вследствие его неуравновешенности совершает пространственное движение. Горизонтальная составляющая, направленная вдоль оси z воспринимается массой 6. Сейсмический датчик преобразует вынужденные колебания массы 6 относительно плиты 2 в ЭДС. полученное значение ЭДС обрабатывается в электронном счетно-решающем устройстве, которое является неотъемлемой частью балансировочного станка. В результате

устройство выдает значения угловой координаты и модуля главного векто-

ра D дисбалансов ротора. После этого оператор устраняет неуравновешенность либо установкой дополнительной массы, либо удалением части

материала /13/.

Для роторов, имеющих значительные размеры вдоль сои вращения, необходима динамическая балансировка, поскольку главный момент дисбалансов будет значительным. Как уже отмечалось выше, такая неуравноr -

вешенность будет выражаться главным вектором дисбалансов D и глав-

ным моментом дисбалансов D . Динамическую неуравновешенность можно условно представитьr r в виде неуравновешенности двух точечных масс и

дисбалансами D1 и D2 /13/.

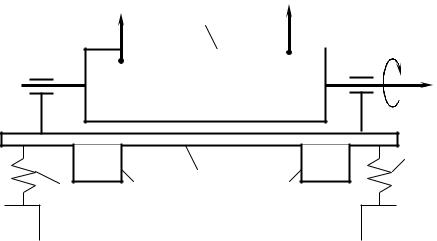
Рассмотрим динамическую балансировку ротора на балансировочном станке (рис. 9.10) у которого ось вращения балансировки ротора совершает пространственное движение. Ротор 1 вращается с постоянной угловой скоростью в подшипниках, смонтированных на плите 2. плита установлена на станине на четырех пружинах 3. На плите 2 установлены два сейсмических датчиках 4 и 5 /13/.

z

Рис. 9.10

В процесс вращения ротора, вследствие его неуравновешенности, ось z и плита 2 совершают пространственное движение. Датчики преобразуют механические колебания и преобразуют их в ЭДС. Счетно-решающее устройство (на рисунке не показано) обрабатывает сигналы с датчиков и вы-

дает отдельно величину дисбаланса D1 и дисбаланса D2 , т.еr. оба дисбаланса определяется одновременно. После определения D1 и D2 оператор

балансирует ротор в плоскостях коррекции удалением (добавлением) материала /13/.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК К ГЛАВЕ 9

1.Васильев Ю.М., Готлиб Я.Г., Филатов А.Е. Нормирование производственных вибраций в СССР и за рубежом. - М.: Машиностроение, 1976. - 20 с.

2.Вибрация в технике: Справочник: В 6 т. Защита от вибрации и ударов /Под ред. К.В. Фролова. - М.: Машиностроение, 1981. - Т.6. - 456 с.

3.Вибрация в технике: Справочник. В 6 т. Колебания машин, конструкций и их элементов/Под ред. Ф.М. Диментберга и К.С. Колесникова. – М.Машиностроение, 1980. –Т.3. – 544 с.

4.ГОСТ 12.1.012-90. Система стандартов безопасности труда. Вибрационная безопасность. Общие требования.

5.ГОСТ 22061-76 Система классов точности балансировки.

6.ГОСТ 25980–83. Вибрация. Средства защиты. Номенклатура параметров.

7.ГОСТ 26568–85. Вибрация. Методы и средства защиты. Классификация

8.Иванов Н.И. Борьба с шумом и вибрациями на путевых и строительных машинах. - М.: Транспорт, 1987. - 223 с.

9.Колесников А.Е. Шум и вибрация. – Л.:Судостроение, 1988. – 247 с.

10.Левитская О.Н., Левитский Н.И. Курс теории механизмов и машин. М.: Выс-

шая школа, 1978. – 269 с.

11.Левитский Н.И. Колебания в механизмах: Учеб. пособие для втузов. – М.: Наука, Гл. ред. физ.-мат. лит., 1988. – 336 с.

12.Снижение динамических воздействий на одноковшовый экскаватор: Монография / В.С. Щербаков, П.А. Корчагин. - Омск: Изд-во СибАДИ, 2000. - 147 с. Теория механизмов и механика машин: Учеб. для втузов/ К.В. Фролов, С.А. Попов, А.К. Мусатов и др.; Под ред. К.В. Фролова М.: Высш. шк., 1998. – 496 с.