Древнерусские меры длины могут быть сведены в следующую таблицу:

Виды саженей	Сажень (в см)	Доли саженей
		1/2	1/4 локоть	1/8 пядь	1/16
Простая, прямая	152,76	76,38	38,18	19	9,5
Мерная, маховая	176,4	88,2	44,1	22	11
«Морская»	~ 183	91,5	45,7	22,8	11,4
«Трубная»	~187	93,5	46,7	23,3	11,6
«Сажень без чети»	197,2	98,6	49,6	24,8	12,4
Косая, казенная	216	108	54	27	13,5
Великая, косая	249,46	124,73	62,36	31,18	15,6

2. Известен ряд случаев, когда одно и то же лицо производило измерение одного и того же объекта одновременно разными видами саженей.

Так, при ремонте Софийского собора в Новгороде в XVII в. измерения велись двумя видами саженей: «А внутри главы кругом где окна - 12 сажен (по 152 см), а от Спасова образа ото лбу до моста церковного - 15 сажен мерных (по 176 см)». Анализ архитектурных памятников XI—XV вв. позволил утверждать, что древнерусские зодчие широко применяли одновременное пользование двумя или даже тремя видами саженей.

3. Непонятное для нас одновременное пользование разными мерами длины объясняется заложенными в этих мерах при их создании строгими геометрическими соотношениями (рис. 34).

Геометрическая сопряженность древнерусских саженей особенно ясна в наименовании «прямой» и «косой» сажени. Оказалось, что прямая сажень есть сторона квадрата, а косая — его диагональ (216 = 152,7√2). Такое же соотношение существует между «мерной» и «великой» (косой) саженями: 249,4 = 176,4√2. «Сажень без чети» оказалась искусственно созданной мерой, являвшейся диагональю половины квадрата, сторона которого равна мерной сажени.

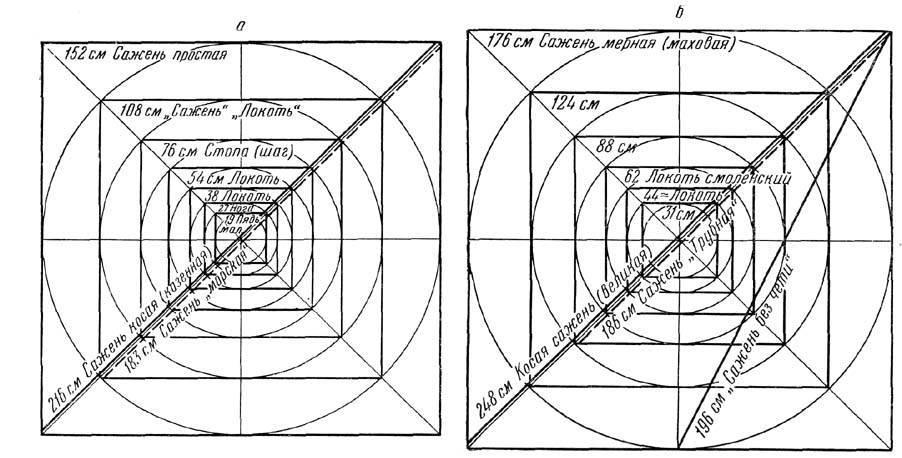
Рис. 34. Графическое изображение русских саженей и их долей по принципу «вавилона» (из статьи Б. А. Рыбакова, 1949)

4. Графическим выражением этих двух систем мер длины (одной, основанной на «простой» сажени, и другой, основанной на «мерной» сажени) являются хорошо известные по древним изображениям «вавилоны», представляющие собой систему вписанных квадратов. Наименование «вавилоны» взято из русских источников XVII в. (см. рис. 34).

5. Дошедшие до нас изображения «вавилонов» (рис. 35) в основе своей являются схемой плана священного храма-зиккурата с его ступенями и лестницами, но почти все они далеки от точности и могли служить лишь каким-то символом, например, символом зодческой мудрости. Этот древний символ давно уже нашел отражение в играх, и нам известны игральные доски, воспроизводящие «вавилон» (игра «мельница»).

Новые находки загадочных чертежей  «вавилонов»  на Таманском городище (древней Тмутаракани) и Старо-Рязанском городище, относящиеся к IXXII вв., позволяют значительно углубить анализ этих чертежей и установить их тесную связь с процессом архитектурного расчета.

Рис. 35. Кирпич IX в. со знаком «вавилона» (Саркел)

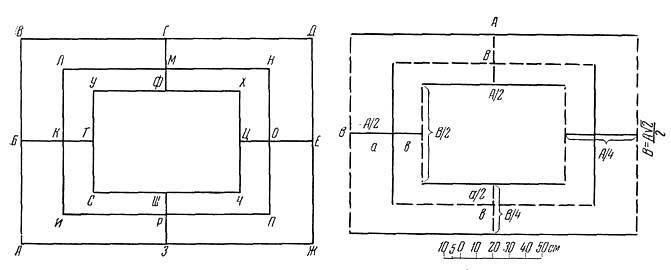
Рис. 36. Прямоугольный «вавилон». Соотношение сторон

«Вавилоны» тмутараканской церкви середины X в. мы должны рассматривать как два сопряженных между собой чертежа: три вписанных квадрата были вспомогательным чертежом (выполненным более небрежно), необходимым для построения второго чертежа, состоящего из прямоугольников.

Каким же целям должен был служить этот сложный чертеж, ради чего создавалась такая геометрическая композиция?

Ответить на эти вопросы можно лишь, ознакомившись с математическими свойствами этого чертежа. Оказывается, что стороны прямоугольников и расстояния между узловыми точками чертежа (углами и пересечениями линий) таят в себе множество различных соотношений, которые известны в архитектуре и прикладной геометрии средневековья.

Обозначим все точки нашей фигуры буквами русского алфавита (рис. 36) и перечислим соотношения линий. В основе фигуры лежат шесть пар прямых линий (сторон прямоугольников), разделенных пополам, и две пары пересекающих их линий, которые разделяются на две неравные части каждая. Если же учитывать не только изображенные на чертеже линии, но и те, которые могут быть проведены от точки к точке, то количество линий возрастет до 42.

Все линии «вавилона» можно подразделить на три группы.

1. Часть линий является долями длинных сторон ВД — АЖ внешнего прямоугольника:

ВГ = ГД = ВД/2 =АЗ = ЗЖ = АЖ/2= ЛИ=НП = УХ = СЧ;

БТ = ЦЕ =ВД/2=ВГ/2 и т. д.

2. Другие линии представляют собой фракции диагонали квадрата, сторона которого равна ВД или АЖ:

АВ=ДЖ=ЛН=ИП=(ВД√2)/2=(АЖ√2)/2;

СУ=ХЧ=АВ/2=ДЖ/2=(ВД√2)/4=(АЖ√2)/4;

ГФ=ШЖ=АВ/4=ДЖ/4=СУ/2=ХЦ/2=(ХФ√2)/2=(БТ√2)/2=(УХ√2)/4=(ВД√2)/8 и т.д.

3. Третья группа самых коротких линий тоже представляет сочетание сторон и диагоналей квадрата; эти линии получены как разность между длинными и короткими сторонами прямоугольников.

БК=ОЕ; ГМ=РЗ=КТ=ЦО=(БК√2)/2=ОЕ√2)/2;

ФМ=ШР=БК/2=ЩУ/2=(ГМ√2)/2 и т.д.

Если для простоты обозначить длинную сторону через А, то при помощи этой величины мы сможем выразить все линии «вавилона». Одни из них будут представлять последовательное деление на 2: А; А/2; А/4, другие могут быть представлены иррационально: (А√2)/2; (А√2)/4; (А√2)/8, третьи являются разностью: А/2 - (А√2)/4; А/4 - (А√2)/4; А/4 - (А√2)/8 (см. рис. 30 справа).

Линии «вавилона» образуют несколько пропорциональных рядов. Вот, например, один из них: МФ/МГ = МГ/БК = ГФ/БТ = УС/УХ = АВ/БД.

Среди линий «вавилона» нетрудно подыскать свыше десятка отношений, очень близких к «золотому сечению»: м/М = М/(м + М). Приближенность решений определяется только при математическом анализе, но практически она неуловима. Наиболее точным является отношение: ВК/АЛ = АЛ/(ВК + АЛ) = АЛ/БД. Здесь суммой двух отрезков является длинная сторона прямоугольника А.

Погрешность равна 0,003 этой стороны; при практических построениях она была мало заметна.

При помощи изучаемого нами графика можно быстро и с достаточной для практических целей точностью решить все важнейшие задачи средневековых геометров. Знаменитый персидский математик Абуль-Вафа, современник древнейших русских церковных построек, переводчик Эвклида и Диофанта (940—998 гг.) посвятил специальную книгу задачам на построение равновеликих фигур. Со всей строгостью настоящего ученого обрушился он на «методы, применяемые рабочими, не основанные на каких-либо началах», и дал взамен их математически безупречные, но необычайно сложные и громоздкие решения этих задач, руководствуясь «началами» Эвклида. Однако не все задачи, интересовавшие тогдашних практиков, могли быть решены строго математически - такова, например, была древняя задача о нахождении геометрическим путем квадрата, равновеликого кругу, задача «квадратуры круга».

Современный Абуль-Вафе тмутараканский график из трех вписанных прямоугольников позволяет с очень большой степенью точности (хотя и не всегда теоретически верно) почти моментально решать все подобные задачи, включая и «квадратуру круга».

Рассмотрим несколько примеров, взяв за основу квадрат, сторона которого равна длинной стороне внешнего прямоугольника «вавилона» (А).

1. Удвоение квадрата (рис. 37): сторона удвоенного квадрата равна удвоенной боковой стороне «вавилона» (т. е. 2 АВ или 2 ДЖ).

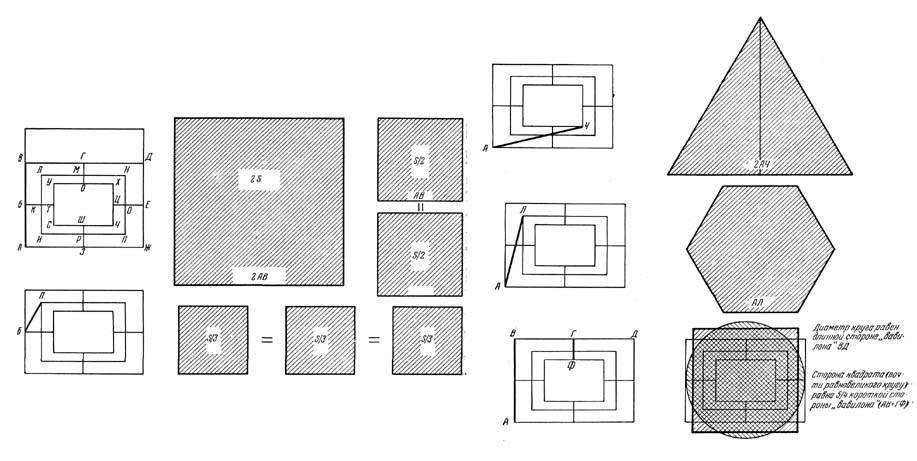
Рис. 37. Решение задач на построение при помощи «вавилона»: удвоение квадрата; деление квадрата на два; деление квадрата на три; построение треугольника, равновеликого квадрату; построение шестиугольника, равновеликого квадрату; приближенное решение квадратуры круга.

2. Построение двух равных квадратов, сумма площадей которых равна площади основного квадрата: сторона каждого малого квадрата равна АВ или ДЖ.

3. Построение трех квадратов на тех же условиях: удвоенная линия БЛ (или три других, ей соответствующих - БИ, БН, БП) является стороной искомого квадрата.

4. Построение равностороннего треугольника, равновеликого квадрату: сторона треугольника равна удвоенной линии АЧ. Высота его будет

равна удвоенной линии ТН.

5. Построение правильного шестиугольника, равновеликого квадрату: стороной шестиугольника будет больший отрезок стороны квадрата, разделенной в «золотом сечении», т. е. линия АЛ.

6. Построение квадрата, равновеликого кругу («квадратура круга»): примем диаметр окружности равным большой стороне «вавилона». Сторона искомого квадрата будет равна сумме боковой стороны «вавилона» и линии ГФ (поперечной линии, соединяющей длинные стороны всех трех прямоугольников). Погрешность здесь будет очень невелика и практически почти неощутима - 0,0023 диаметра; ошибки в задачах 3 и 5 тоже очень малы и не превышают 0,005-0,003. Наименее точно решение задачи 4 (ошибка равна 0,08). Задачи 1, 2 решаются точно.

Зная свойства «вавилона», можно было быстро, не производя ни расчетов, ни геометрических построений, сразу же разделить локоть в отношении «золотого сечения», найти фигуры, равновеликие квадратному локтю, дать несколько пропорциональных рядов, дать графическое изображение ряда иррациональных величин: а, a, a, a, a...

Неудивительно, что этот математически универсальный замечательный график мог стать еще в глубокой вавилонской древности символом зодческой мудрости, «хытрости храмоздательской» (рис. 38, 39) [7].

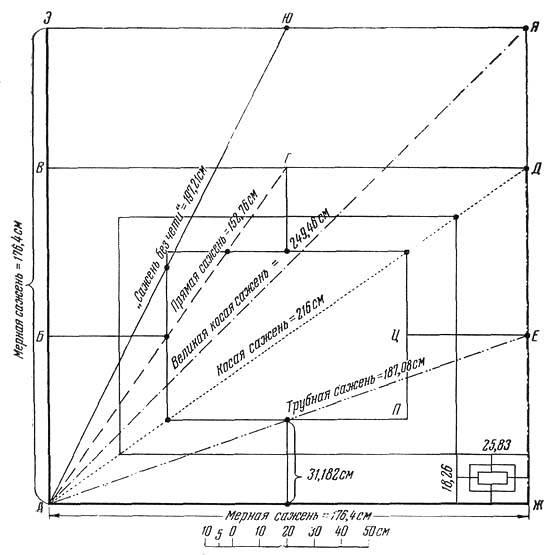
Рис. 38. Единая геометрическая система древнерусских мер длины

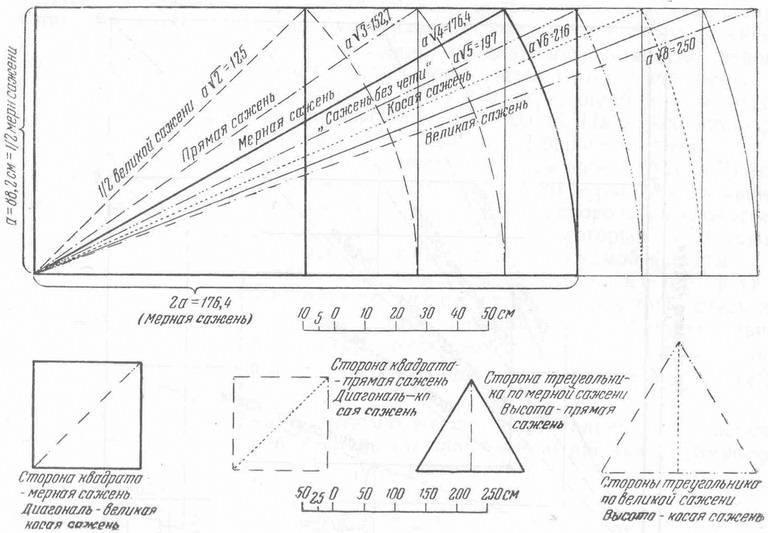
Рис. 39. Геометрические взаимоотношения древнерусских мер

По мнению И.Ш. Шевелева, можно представить себе примерную схему разбивки плана храма.

1. На приготовленной выровненной площадке устанавливаются по странам света оси храма. Их перекрестие дает центр построения, который может быть использован для отсчетов размеров.

2. Специально изготовленными эталонами длины, в связь размеров которых заложена основная соразмерность постройки, размечается положение наружных стен храма, причем западная ветвь оси храма устанавливается более протяженной, чем восточная.

Развитие внутреннего пространства в направлении север-юг определяется взаимосвязью размеров поперечных пространств. Чтобы достичь композиционного единства, мастер должен установить соответствие в ширине западной и восточной травей (рис. 40), прибавить к ним с востока глубину алтаря и с запада - ширину нартекса (рис. 41). Эти размеры обычно также подчинены размерам ядра храма. Но, кроме того, в сумме они ограничены положением уже намеченных наружных стен храма. Поэтому возможны некоторые неувязки между первоначально определенной длиной храма и длиной, полученной вследствие уточнения взаимодействия внутренних размеров.

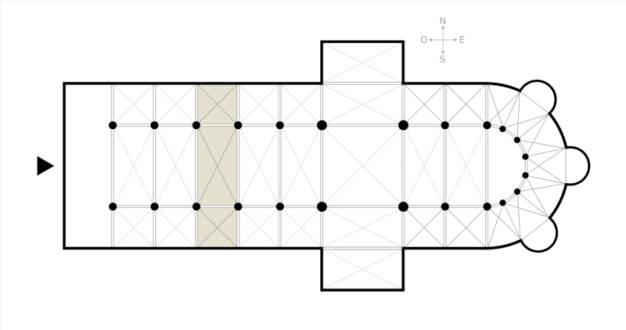
Рис. 40. Траве́я

Траве́я (фр. travée — пролет, ряд, лат. trabs — балка, деревянная кровля, пролет) — структурная секция внутреннего пространства нефа в некоторых христианских храмах. Как правило, имеет прямоугольную форму, ограниченную четырьмя (шестью) устоями, на которые опираются пяты арок, таким образом нервюры крестовых или стрельчатых сводов оказываются параллельными, что придаёт подобной планировке (называемой "связанной системой") свода большую прочность.

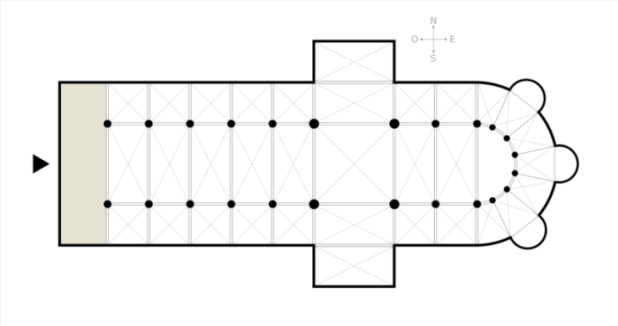
Рис. 41. Нартекс на условной схеме западноевропейского храма

Нартекс (от греч. νάρθηξ — ларчик, шкатулка гр. νάρθξ) — притвор храма или внутренняя закрытая, паперть-вестибюль, расположенный между атриумом (если он был) и наосом византийского храма, в древнехристианских храмах (базиликах) притвор, род сеней при входе в храм, в которых, при богослужении, стояли оглашенные, воссоединяемые с церковью, кающиеся и бесноватые; располагается с западной стороны и изнутри полностью открыт в основной объем храма.

Современный архитектор определяет размеры каждого элемента своего произведения в зависимости от его назначения, материала и конструкции. Он выражает их величины в отвлеченных измерениях метрической системы мер и фиксирует на чертеже. Строители, возводя постройку, соизмеряют величины ее элементов с чертежом и условной единицей - метром, а не в отношениях одного к другому. Таким образом, соразмерность потеряла свое прежнее практическое значение. И если в прошлом несоразмерная постройка была невозможна технически, то теперь строительный процесс не контролирует гармоничность частей сооружения. Правда, десятичная система исчисления, а также чертежные угольники в 45⁰ и 60⁰. которыми пользуются архитекторы, уже сами по себе вносят в каждый чертеж определенное единство масштаба и пропорций. Применяя пропорциональный циркуль, установленный в золотом сечении, и ограниченное число модульных размеров, можно сознательно получить желаемые соотношения. Применение компьютеров во многом лишило архитекторов и этой возможности. Отсюда возникла необходимость уделять большое внимание гармонизации при разработке архитектором проекта сооружения.

3. Определяются прямоугольник, очерчивающий столбы, толщина столбов и подкупольный прямоугольник. Эта операция имеет решающее значение для композиции внутреннего пространства храма: она устанавливает ширину пересекающихся в центре и образующих форму креста главного нефа и трансепта, определяя их взаимосвязь и связь в ширине продольных нефов (главного с боковыми). Одновременно с этим чертеж ядра на земле определил связь диаметра купола с размерами храма в плане, взятыми по стенам четверика.

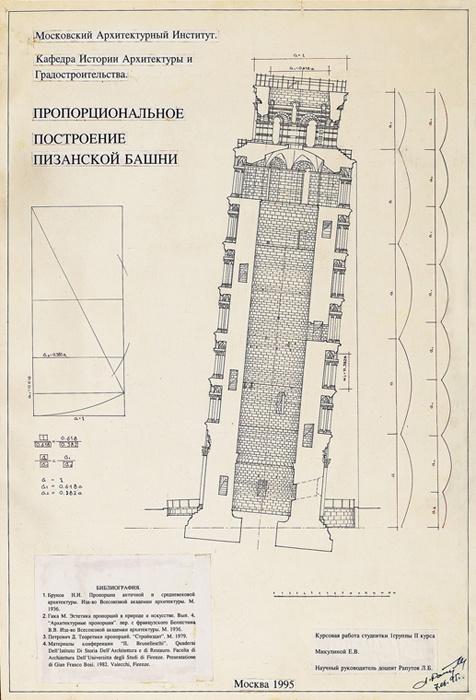
Рис. 42. Анализ соразмерностей и пропорций. Автор Микулина Е.В. Научный руководитель Рапутов Л.Б., 1995 г., МАРХИ

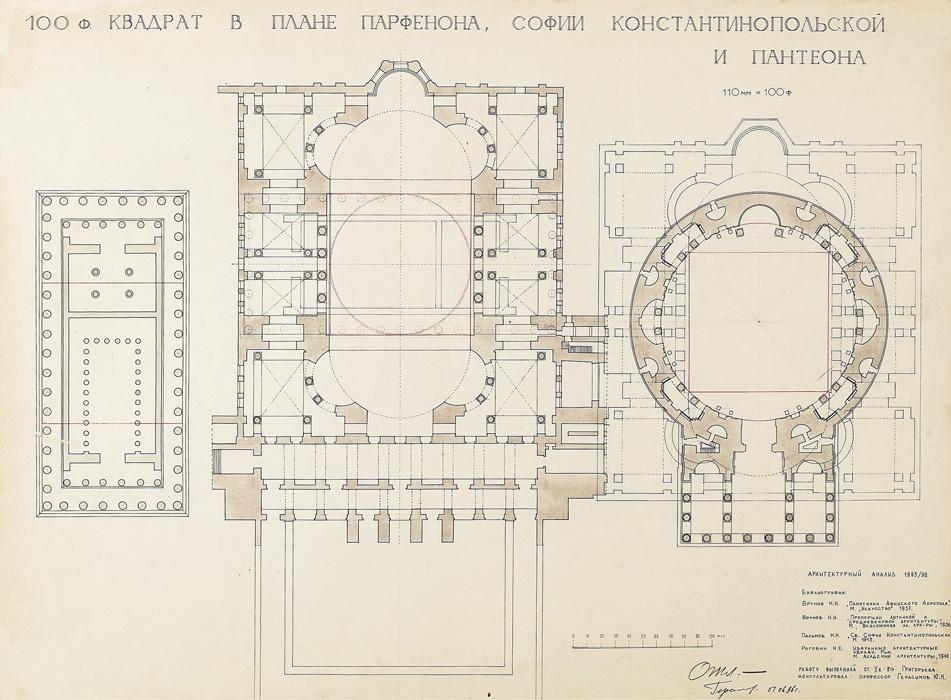
Рис. 43. Анализ соразмерностей и пропорций. Автор Григорьева. Научный руководитель Герасимов Ю.Н., 1996 г. МАРХИ

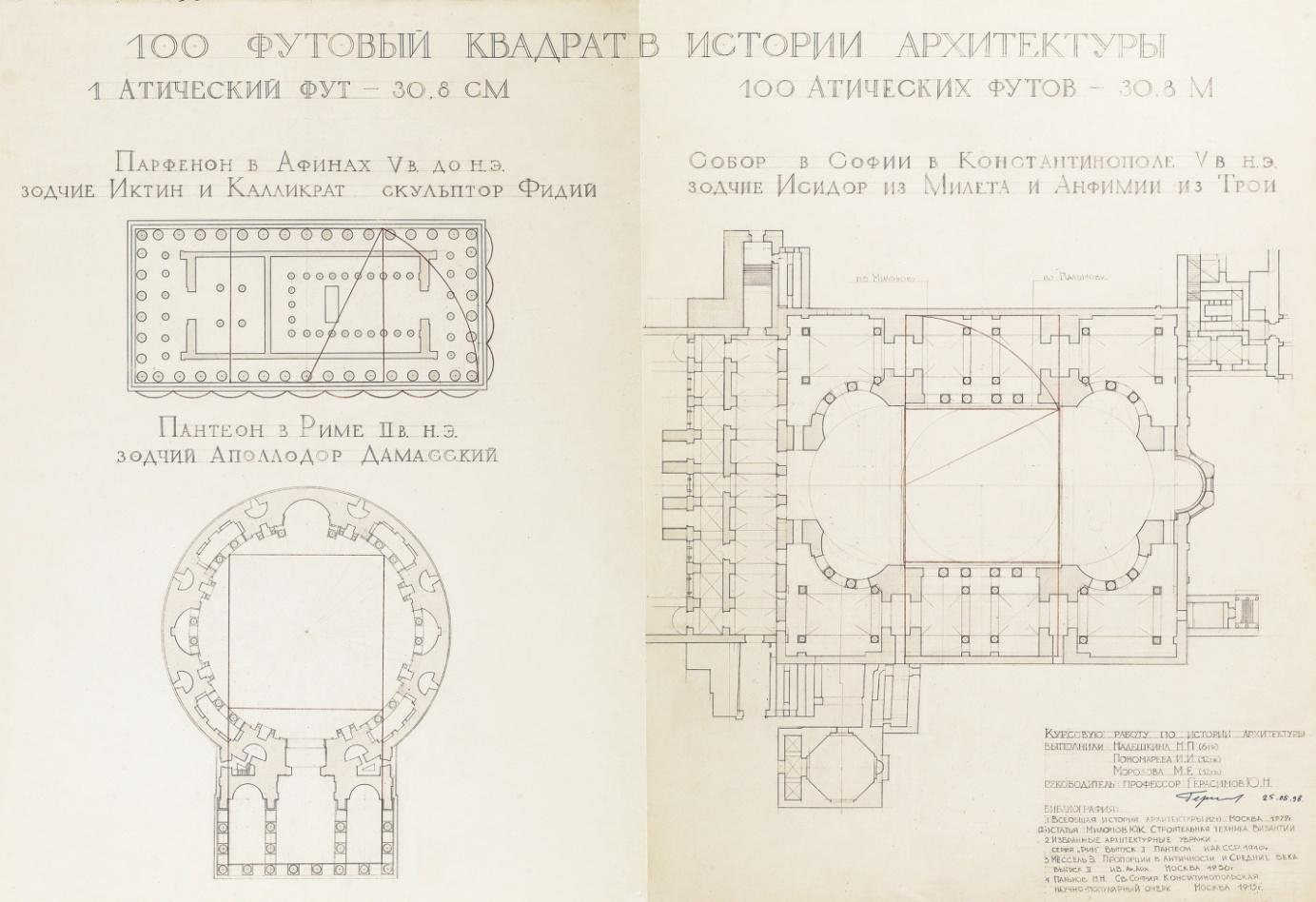
Рис. 44. Анализ соразмерностей и пропорций. Автор Надешкина Н.П., Пономарева И.И., Морозова М.Е. Научный руководитель Герасимов Ю.Н., 1998 г. МАРХИ

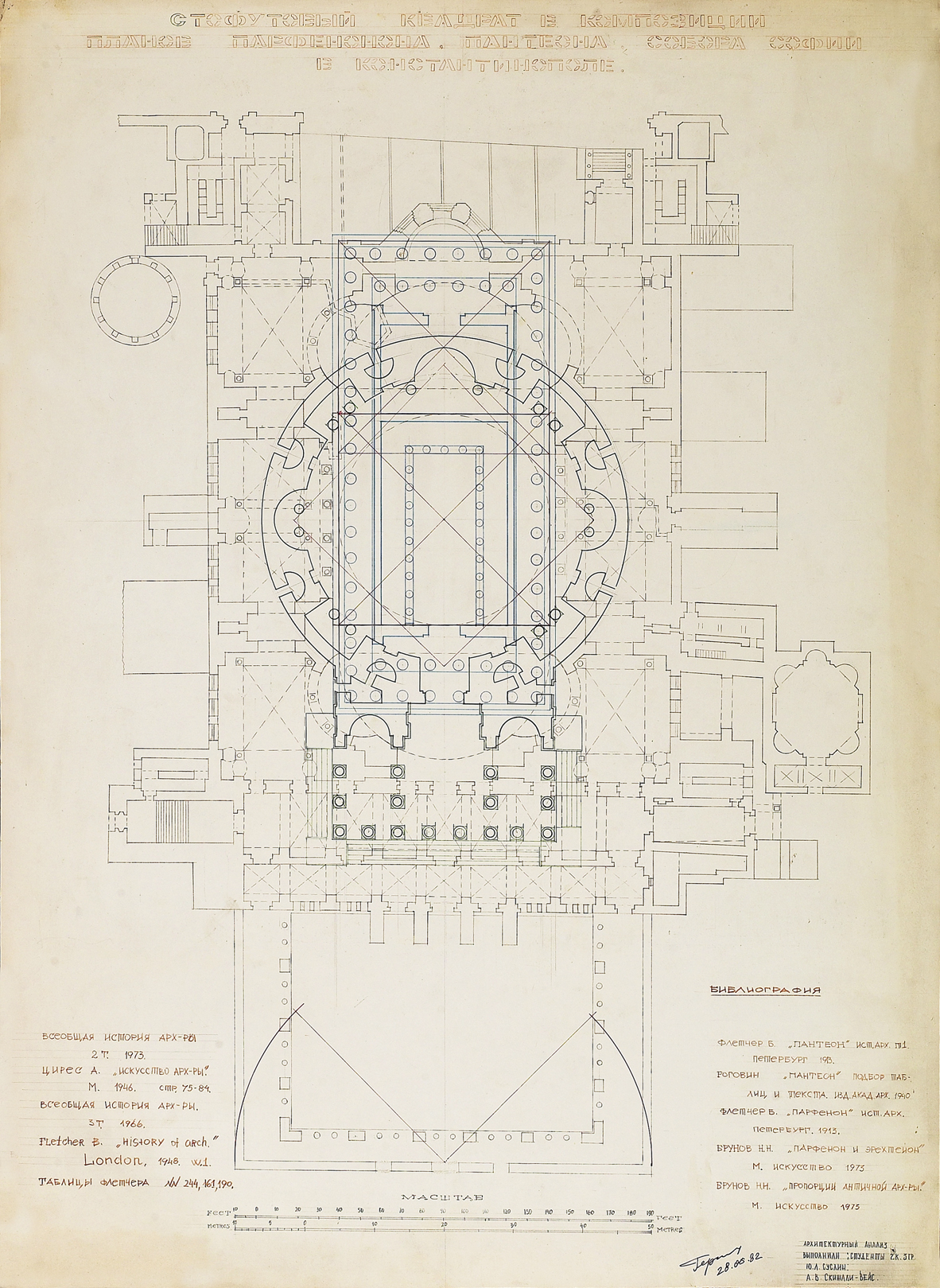
Рис. 45. Анализ соразмерностей и пропорций. Автор Суслин Ю.Л., Скижали-Вейс А.В. Научный руководитель Герасимов Ю.Н., 1982 г. МАРХИ

Рис. 46. Анализ соразмерностей и пропорций. Автор Шакурова Е.А, Николаенко Е.А. Научные руководители Герасимов Ю.Н., Рапутов Л.Б., 1988 г. МАРХИ

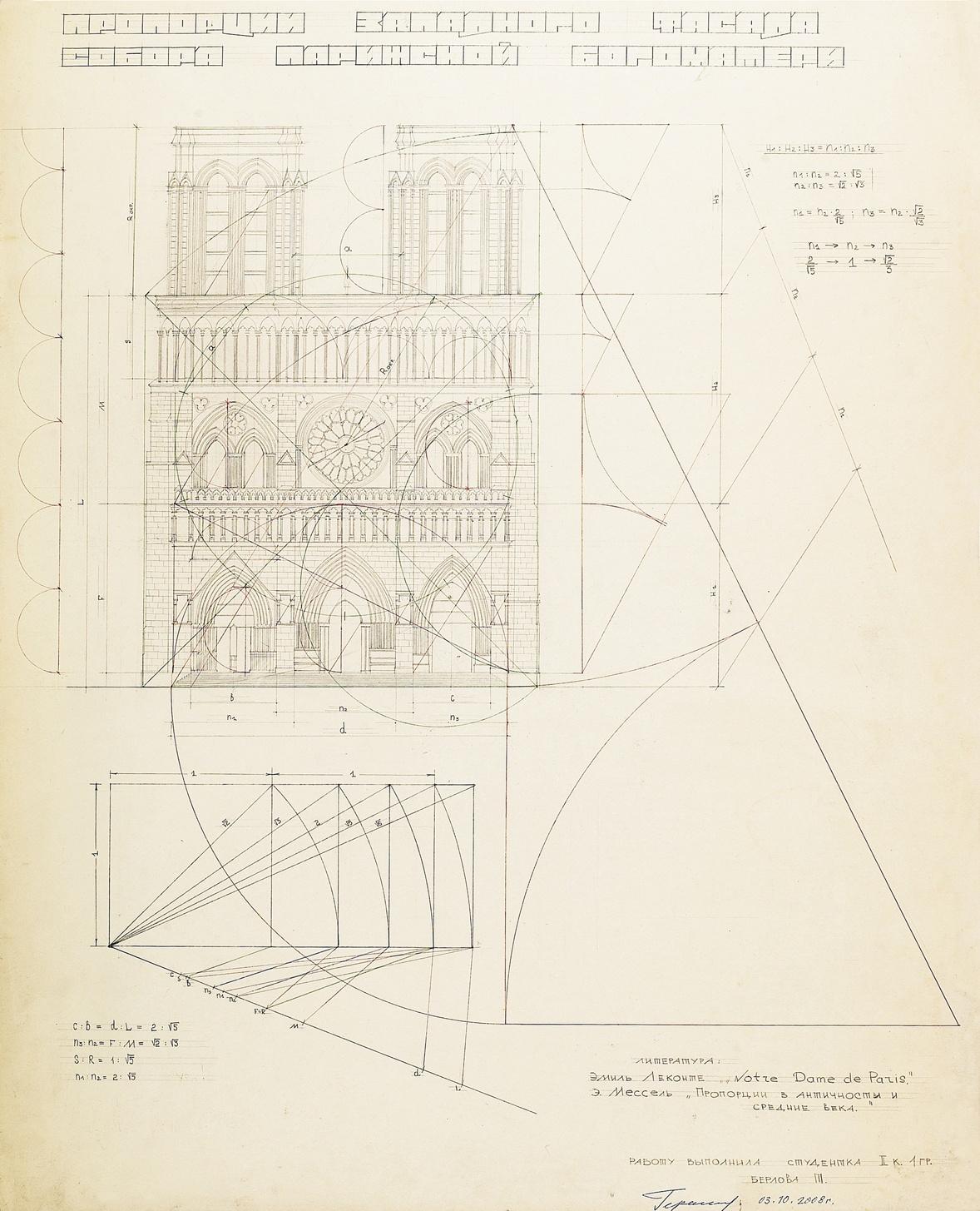
Рис. 47. Анализ соразмерностей и пропорций. Автор Берлова Т. Научный руководитель Герасимов Ю.Н., 2008 г. МАРХИ

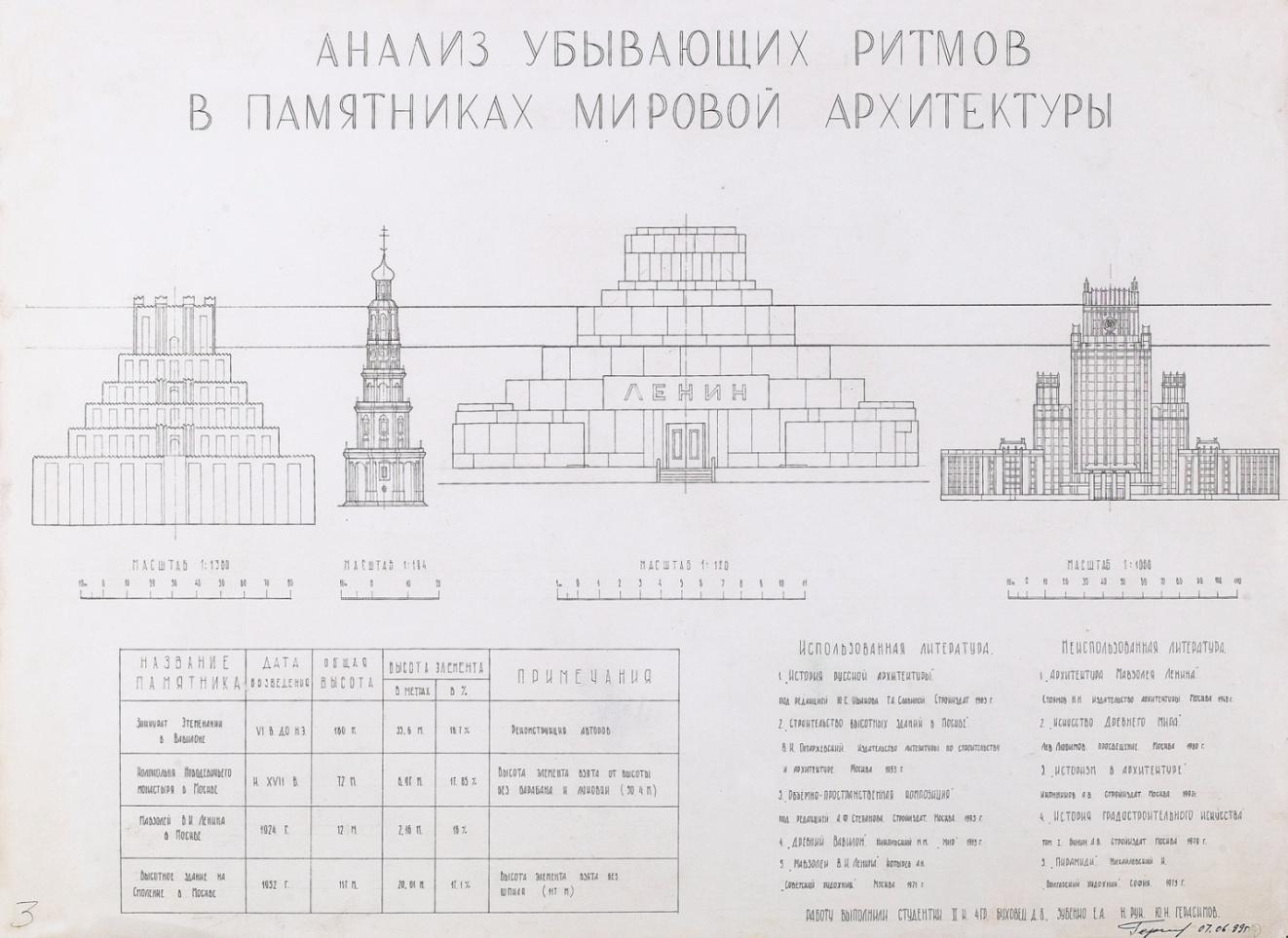
Рис. 48. Анализ метроритмических закономерностей. Авторы Буховец Д.В., Зубенко Е.А. Научный руководитель Герасимов Ю.Н., 1999 г. МАРХИ

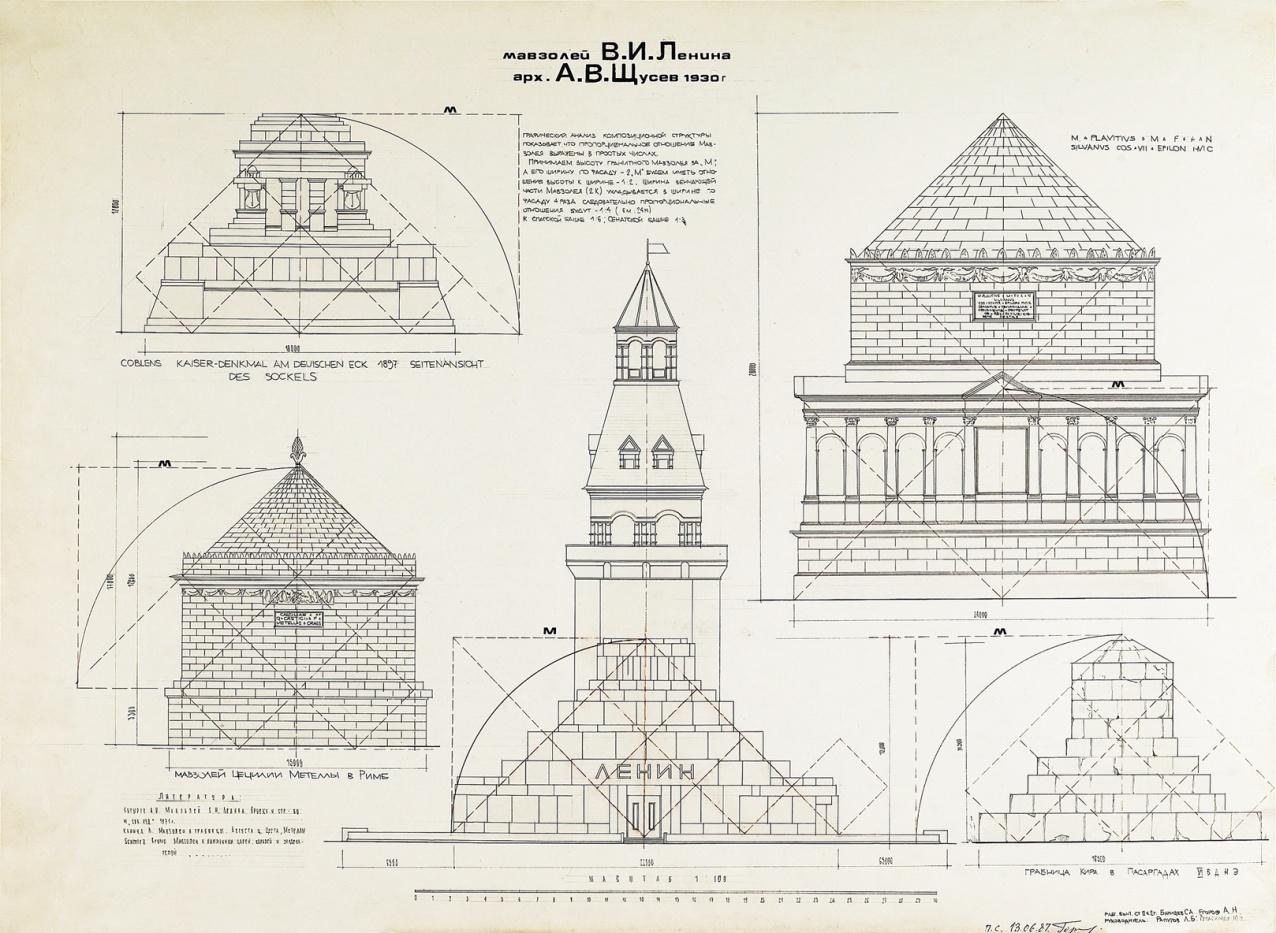
Рис. 49.Анализ соразмерностей и пропорций. Работу выполнили Батищев С.А., Егоров А.Н. Научные руководители: Рапутов Л.Б., Герасимов Ю.Н., 1987 г. МАРХИ

Рис. 50. Анализ соразмерностей и пропорций. Авторы Власова М.А. Колганова С.А. Научный руководитель Герасимов Ю.Н., 1993 г. МАРХИ

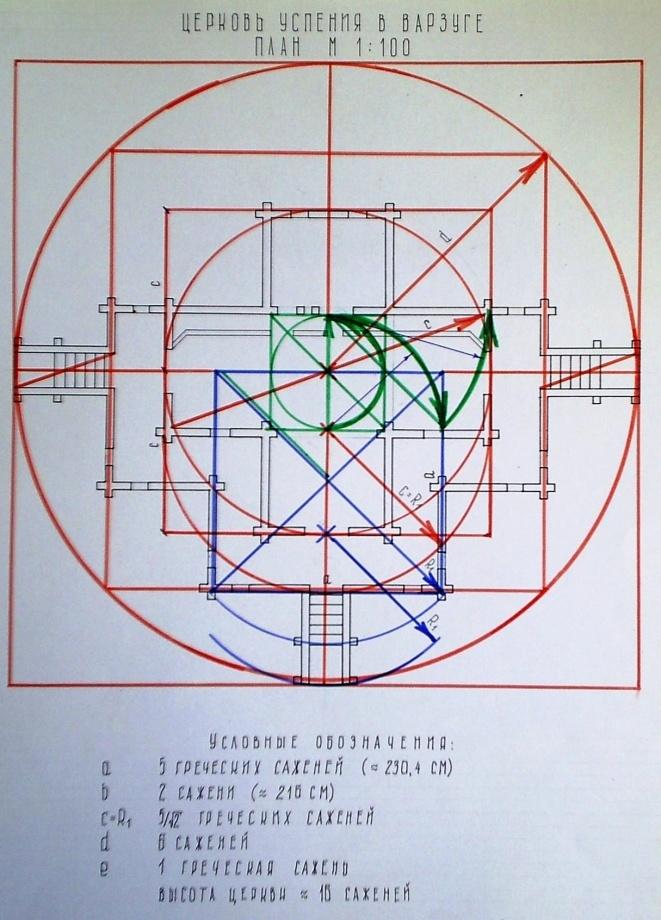
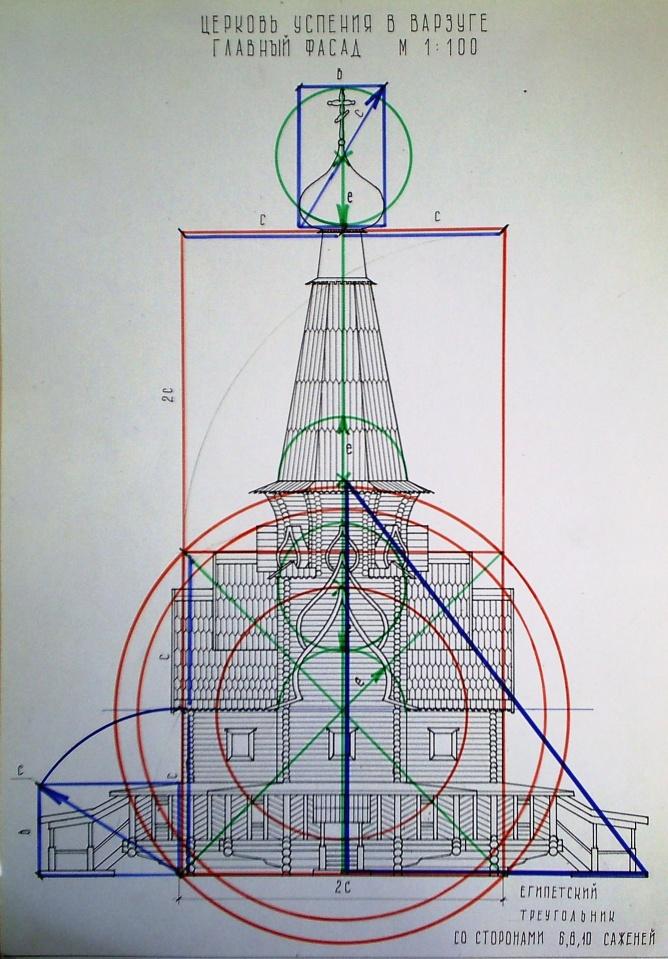
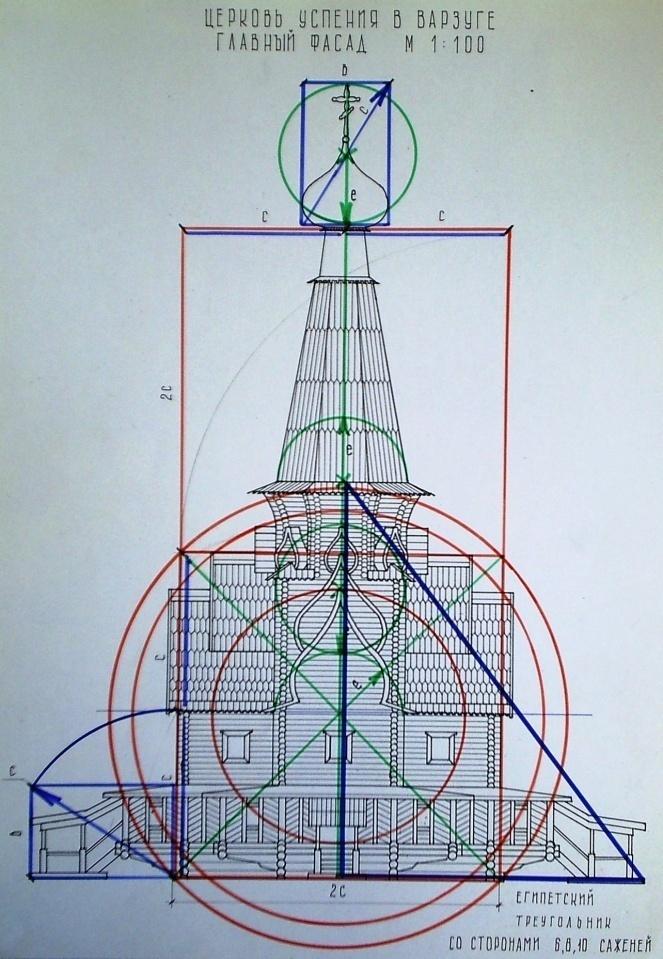
Рис. 51. Анализ соразмерностей и пропорций.

Автор Гордок Е. Руководитель Титова Е.А. 2010 г. СибАДИ

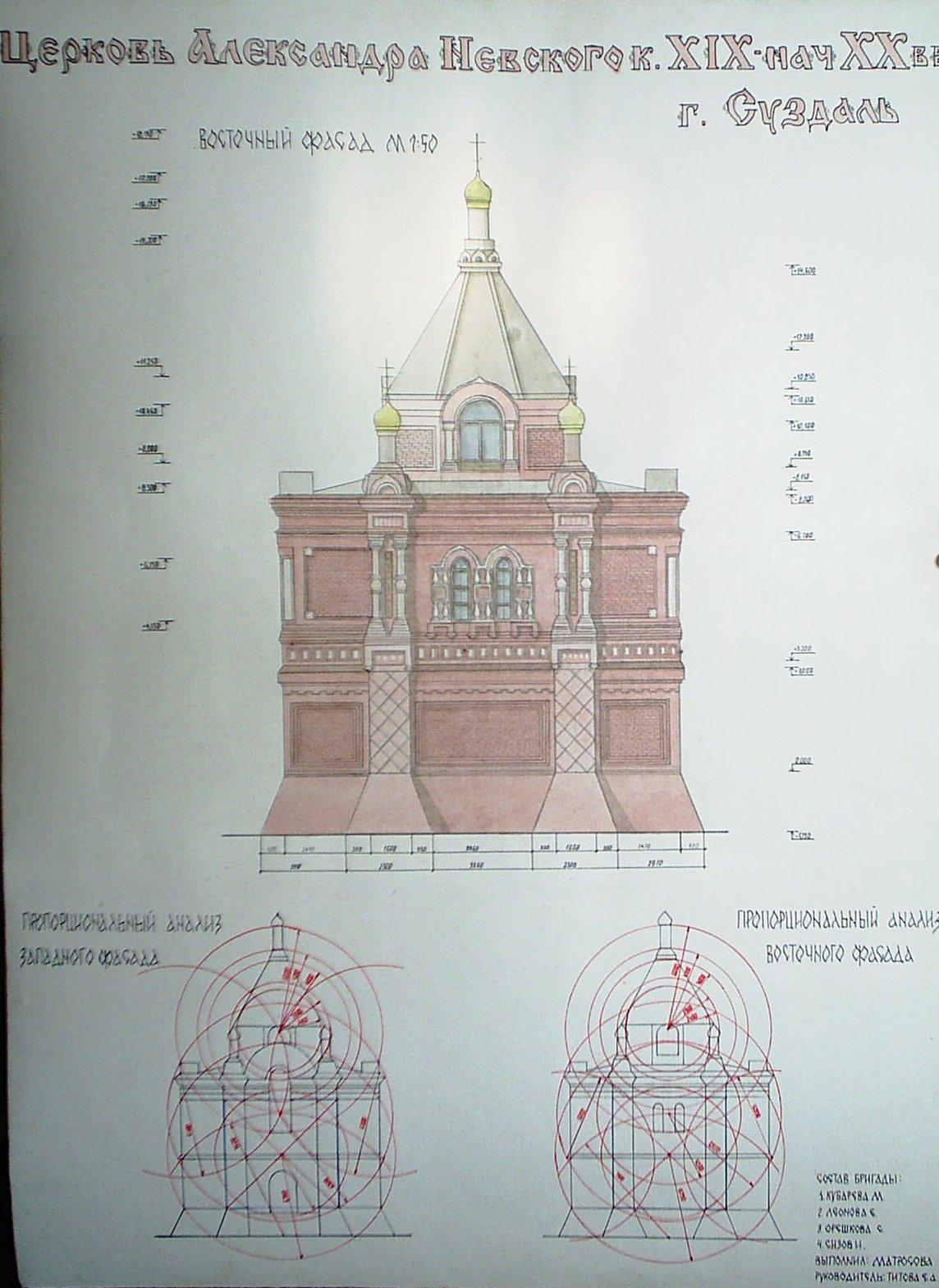
Рис. 52. Обмерные чертежи с анализом соразмерностей и пропорций.

Автор Матросова Е. Руководитель Титова Е.А. 2010 г. СибАДИ

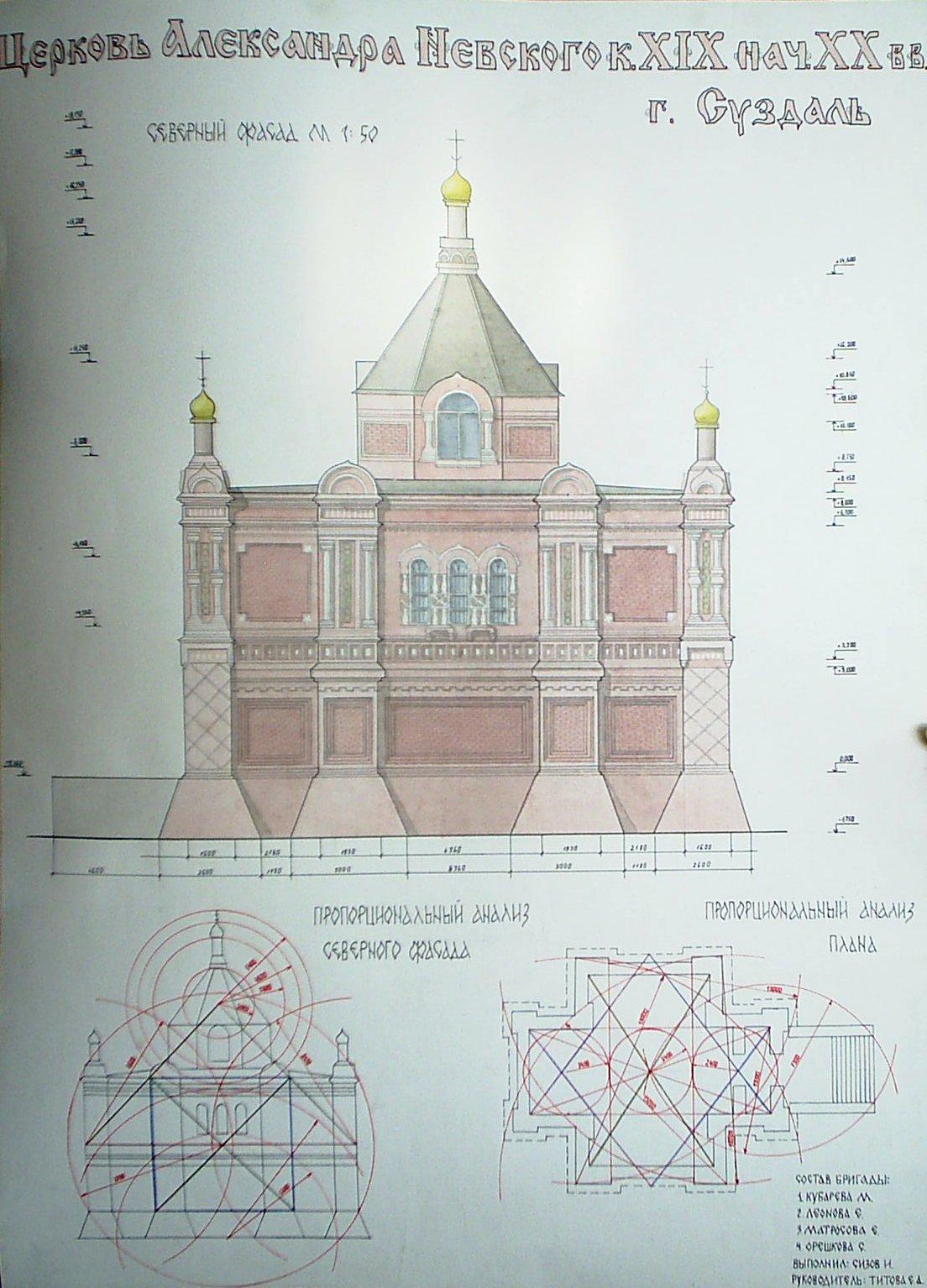
Рис. 53. Обмерные чертежи с анализом соразмерностей и пропорций.

Автор Сизов И. Руководитель Титова Е.А. 2010 г. СибАДИ

Рис. 54. Обмерные чертежи с анализом соразмерностей и пропорций.

Автор Клещенок Е. Руководитель Титова Е.А. 2010 г. СибАДИ

Рис. 55. Обмерные чертежи с анализом соразмерностей и пропорций.

Автор Бадмаева Р. Руководитель Титова Е.А. 2010 г. СибАДИ

Рис. 56. Анализ соразмерностей и пропорций.

Автор Кравец Н. Руководитель Титова Е.А. 2011 г. СибАДИ

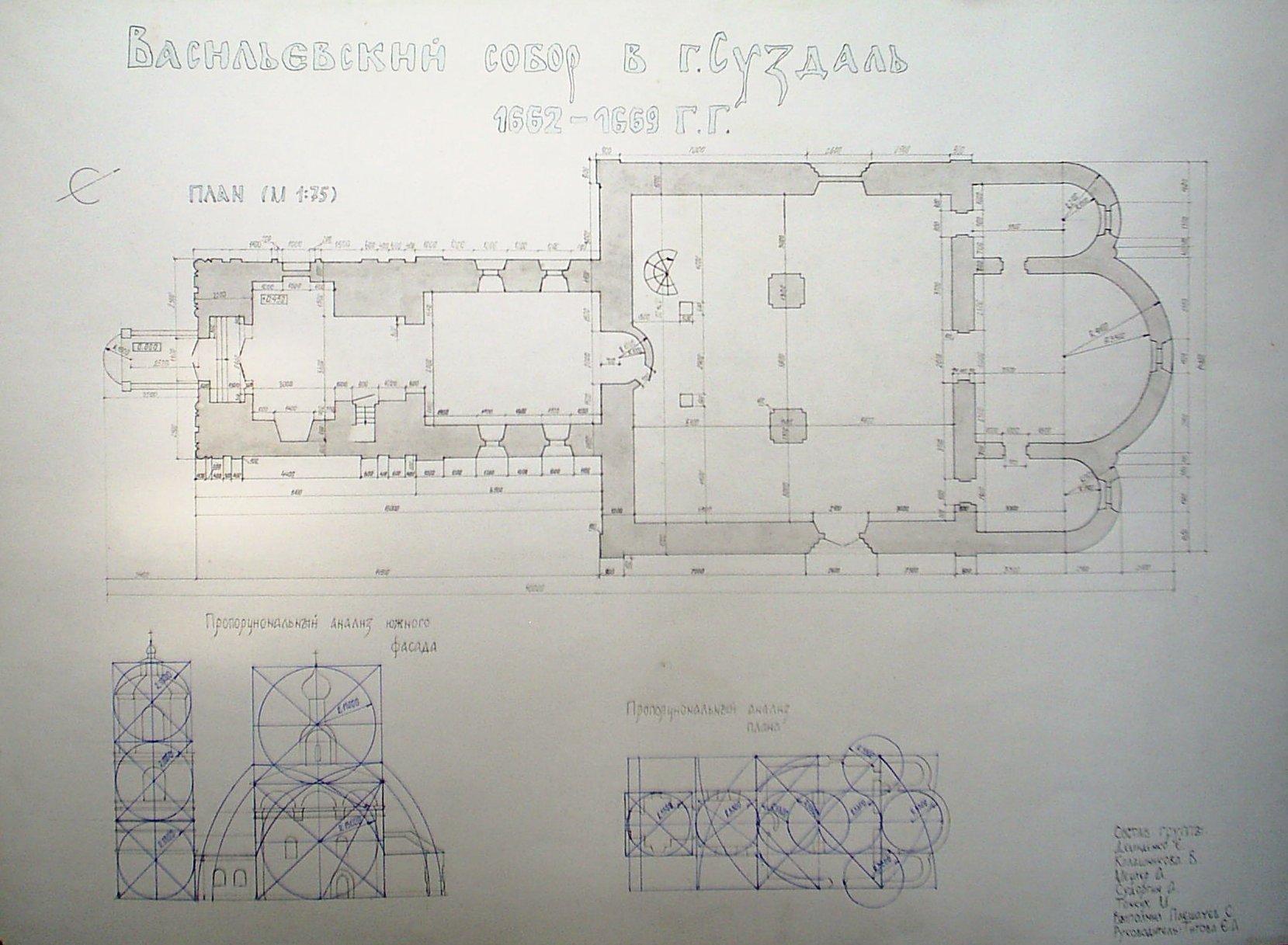
Рис. 57. Обмерные чертежи с анализом соразмерностей и пропорций.

Автор Плешачев С. Руководитель Титова Е.А. 2010 г. СибАДИ

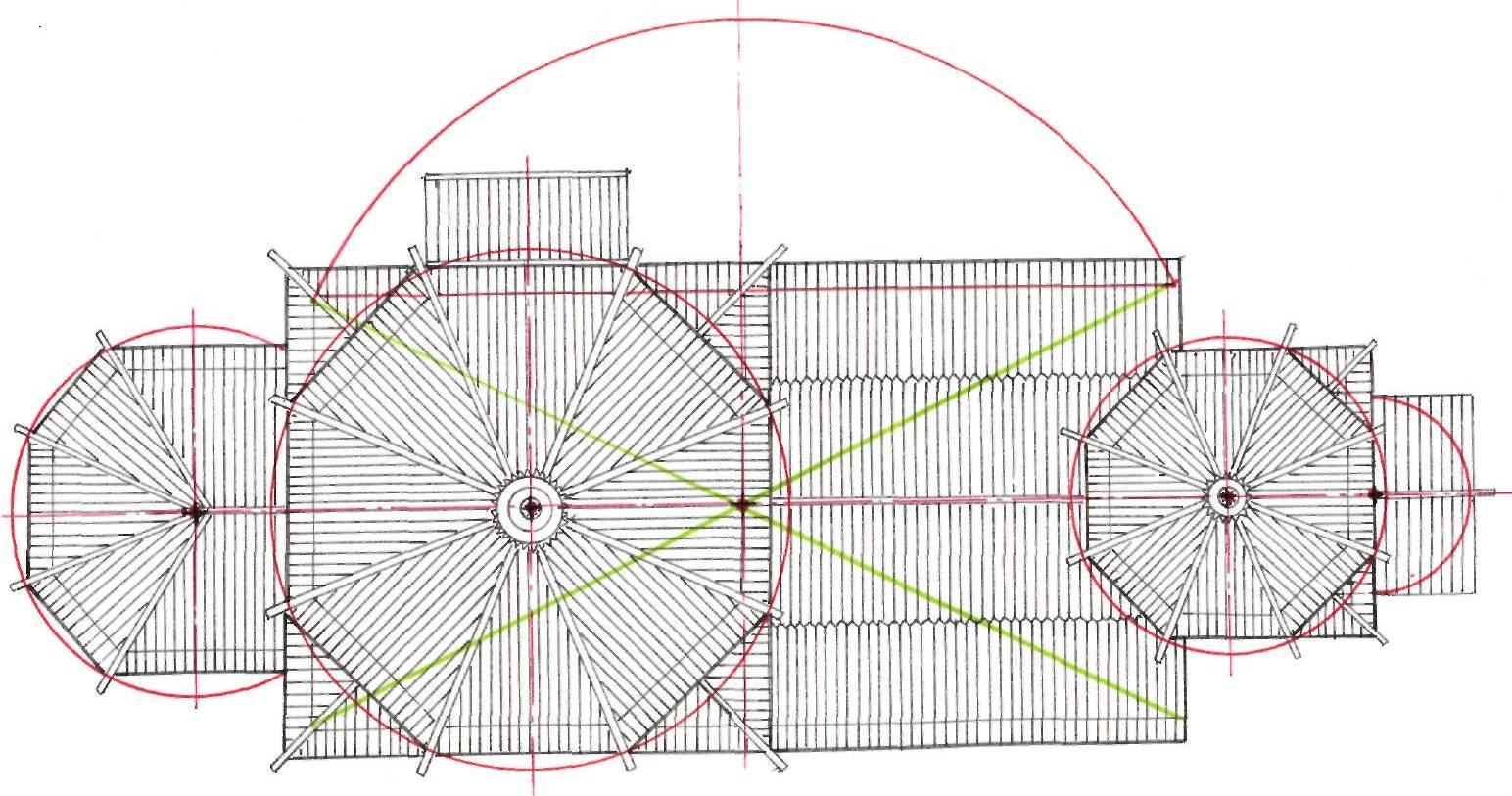
Рис. 58. Геометрический анализ пропорций церкви села Потакино. Автор: Шумилин Антон. Руководитель ст. преп. Титова Е.А. СибАДИ

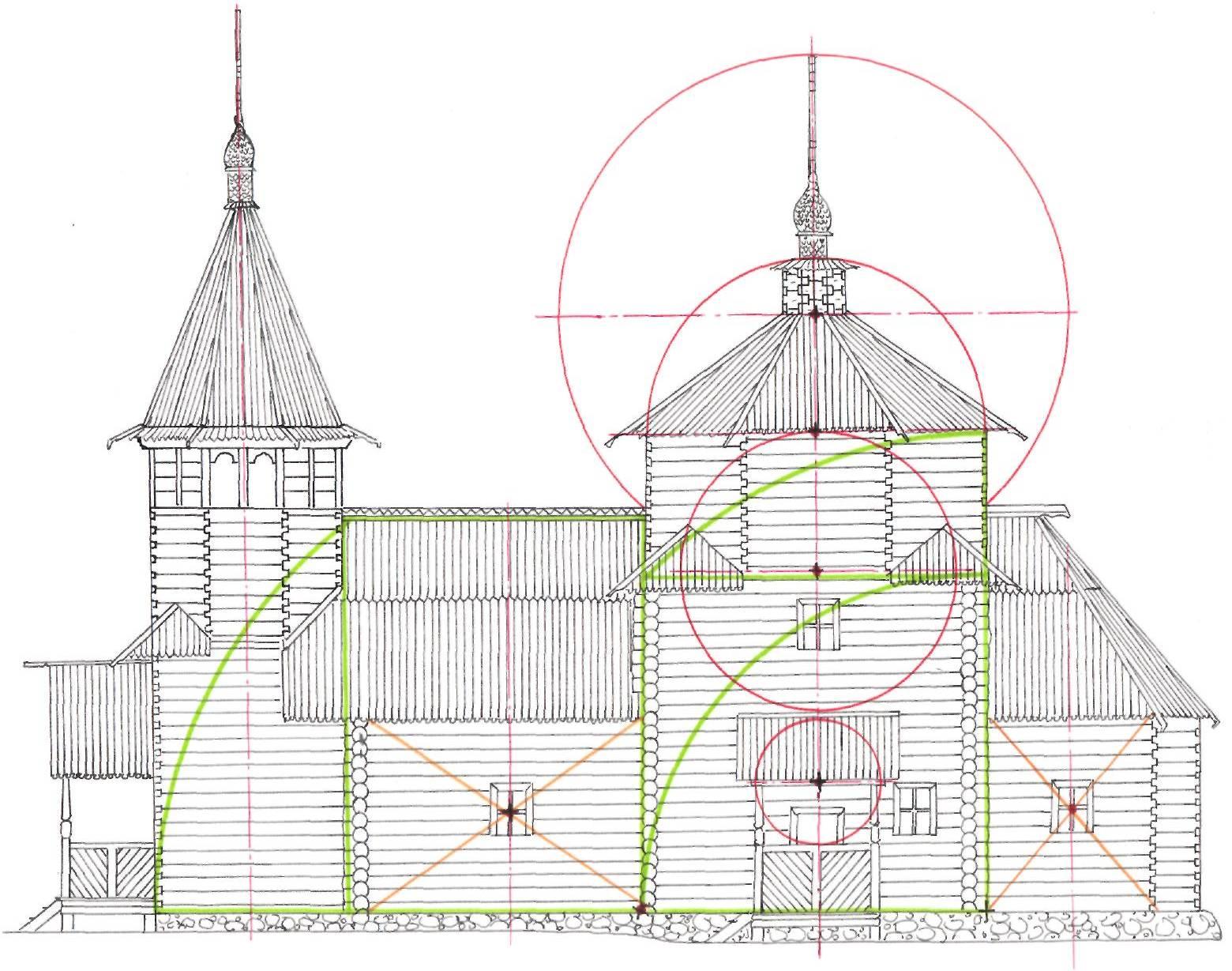
Главный фасад

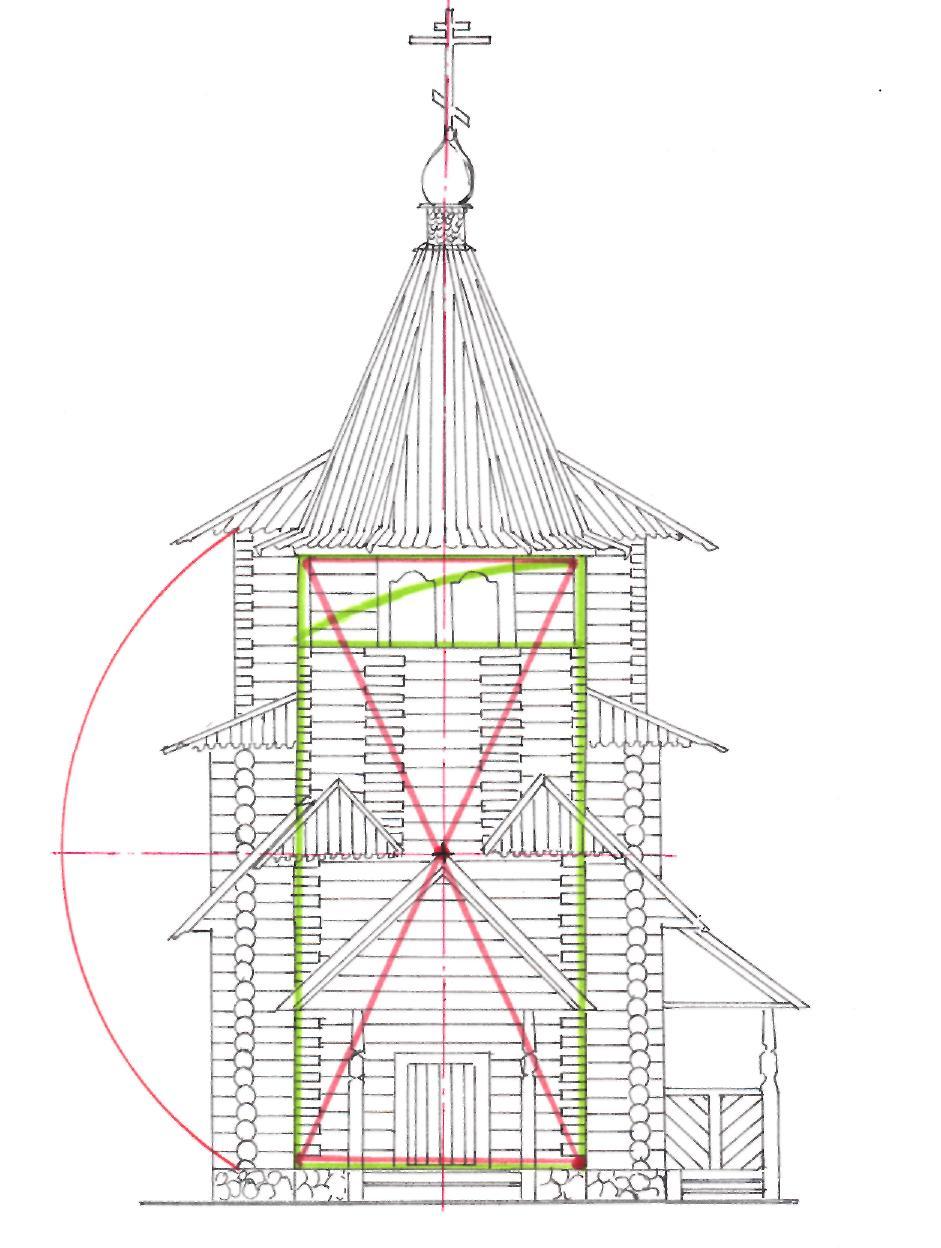
Рис. 59. Геометрический анализ пропорций церкви села Потакино. Автор: Шумилин Антон. Руководитель ст. преп. Титова Е.А. СибАДИ

Список литературы

1. Седова, Л.И. Основы композиционного моделирования в архитектурном проектировании [Текст]: учеб. пособие для вузов / Л.И. Седова; авт. вступ. ст. Л.И. Седова; М-во образования Рос. Федерации, Урал. гос. арх.-худ. акад. Екатеринбург: Издво УралГАХА, 2004.  129 с.: ил., 20 см.  Библиогр.: с.125128.  500 экз.  ISBN 5740800714.

2. Степанов, А.В. Объемно-пространственная композиция [Текст]: учеб. для вузов /А.В.Степанов, В.И. Мальгин, Г.И. Иванова и др.; под общ. ред. А.В.Степанова; авт. вступ. ст. А.В.Степанов; М-во образования Рос. Федерации.  Изд. 3-е, стер. – М.: Архитектура–С, 2004. – 256 с.: ил.; 25 см.  (Специальность «Архитектура»).  Библиогр.: с.255.  Предм. указ.: с. 254.  3000 экз.  ISBN 5964700039 (в пер.).

3. Черняев, А.Ф. Золото Древней Руси. Русская матрица – основа золотых пропорции [Текст] / А.Ф. Черняев; - М.: Белые альвы, 1998. - 144с.: ил. 25 см. - ISBN 5-7619-0062-9.

4. Шевелев, И.Ш. Принцип пропорции: о формообразовании в природе, мерной трости древнего зодчего, архитектурном образе, двойном квадрате и взаимопроникающих подобиях [Текст] / И.Ш. Шевелев; - М.: Стройиздат, 1986. – 200 с.: ил., 23 см. – 15000 экз.

5. Шевелев, И.Ш. Золотое сечение: три взгляда на природу гармонии [Текст]: научное издание / И.Ш. Шевелев, Марутаев М.А., И.П. Шмелев; - М.: Стройиздат, 1990. – 343 с.: ил., 27 см. – 20000 экз. - ISBN 5-274-00197-1 (в пер.).

6. Шевелев, И.Ш. Геометрическая гармония: опыт исследования пропорциональности в архитектуре [Текст] / И.Ш. Шевелев; - Кострома.: Областная типография им. М. Горького Костромского полиграфиздата, 1963. – 109 с.: ил., 23 см. – 1500 экз.

7. Рыбаков, Б.А. Архитектурная математика древнерусских зодчих [Текст]: /Б.А. Рыбаков; Советская археология. № 1, 1957 г.

8. Гримм, Г.Д. Пропорциональность в архитектуре [Текст] / Г.Д. Гримм; Главная ред. строит. лит-ры. - М.: Л.: 1935. – 148 с.: ил.; 20 см – 6000 экз.

9. Калмыкова, Н.В., Максимова. И.А. Макетирование из картона и бумаги [Текст]: учеб. пособие – Изд. 3-е / Н.В. Калмыкова, И.А. Максимова. – М.: Издательство «КДУ», 2007. – 80 с., ил.: 24 см.  10000 экз.  ISBN 978-5-98227-138-9.

10. Стасюк, Н.Г. Основы архитектурной композиции [Текст]: учеб. пособие для вузов / Н.Г. Стасюк, Т.Ю. Киселева, И.Г. Орлова; М-во образования Рос. Федерации, моск. арх. инс./гос. акад/.  Изд. 2е, стер.  М.: АрхитектураС, 2004, 96 с.: ил.; 30 см.  Библиогр.: с.9495.  10000 экз.  ISBN 5964700063.

11. Скуратовский, Г.М. Искусство архитектурного пропорционирования [Текст]: научное издание / Г.М. Скуратовский; - Новосибирск: Наука. Сиб. предприятие РАН, 1997. - 184 с. – 1000 экз. - 15ВК 5-02-031757-8.

12. Чинь, Ф.Д.К. Архитектура, форма, композиция [Текст]: учеб. для вузов / Ф.Д.К. Чинь;  Изд. 3-е, доп. – М.: АСТ, 2005. – 432 с.: ил.; 29 см.  (Специальность «Архитектура»).  3000 экз.  ISBN 978-5-17-053939-0 (в пер.).

13. Кудряшов, К.В.. Архитектурная графика [Текст]: учебн. пособие для вузов / К.В. Кудряшов; М-во образования Рос. Федерации.  Изд. 3-е, стер. – М.: Архитектура–С, 2006. – 312 с.: ил.; - Прил.:с. 248-301.-Библиогр.: с.302. - 25 см.  (Специальность «Архитектура»).  Библиогр.: с.255.  Предм. указ.: с. 254.  3000 экз.  ISBN 5-9647-0020-9 (в пер.).

14. http://marhiv.ru/glavnaya.htm

15. http://www.patriarchia.ru/db/text/142154.html

©Е.А.Титова