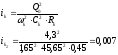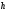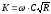2.2.2. Определение критического уклона

м

• 

Площадь живого сечения при критической глубине быстротока 0,75 м .

м

• 

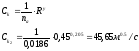
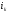<- бурное состояние потока

2.2.3. Определение нормальной глубины

Таблица 4. Определение расходных характеристик

Расчетные формулы	Ед. изм.	Назначаемые и определяемые величины
	м	0,8	0,9	1,0
	м2	1,76	1,98	2,2
	м	3,8	4,00	4,2
	м	0,463	0,495	0,524
	м0,5/с	45,91	46,55	47,09
	м3/с	54,98	64,85	74,99

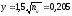
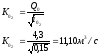График

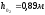По графику определяем, что- нормальная глубина

Глубина в конце входной части (на изломе) h_изл принимается равной критическойh_к , а при более чем двукратном превышении критической глубины над нормальной глубиной на водоскате, глубина на изломе дна равна.

Сравнивая и, назначаемм .

2.2.4. Расчет кривой свободной поверхности на быстротоке

Исследуя дифференциальное уравнение неравномерного движения в призматических руслах

, где (2.25)

П_к– параметр кинетичности,

можно сделать вывод о типе и форме кривой свободной поверхности на быстротоке.

Существует несколько методов расчёта кривой свободной поверхности на водоскате быстротока: Б.А. Бахметева, метод акад. Н.Н. Павловского и другие. В практике дорожно-мостового и аэродромного строительства приходится решать задачи по расчёту неравномерного плавноизменяющегося движения воды не только в призматических руслах, но и на непризматических участках каналов. Поэтому используется универсальный метод конечных разностей В.И. Чарномского..

Метод В.И. Чарномского заключается в следующем: зная глубину в одном из сечений канала, например глубину на изломе дна подводящего канала и лотка быстротока h_n=h_изл, задаёмся значением глубины в соседнем сечении и находим искомое расстояниеΔl между двумя соседними сечениями с известными глубинами по уравнению:

, где (2.26)

ΔЭ– изменение удельной энергии сечения в пределах выбранного участка;

i_тр- уклон трения (среднее значение гидравлического уклона в пределах рассматриваемого участка).[2].

рис.5

1) 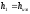=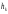*0.8=0,75*0,8=0,6 м;- последняя глубина на быстротоке принимается на 5% больше нормальной глубины, т.е.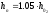; промежуточные глубины рекомендуется задавать с интервалом 0.1 м, опираясь на удобные при последующем построении числовые значения глубин.

2) , т.к. лоток прямоугольной формы и коэффициент откосаm= 0;

3) , т.к. лоток прямоугольной формы и коэффициент откосаm= 0;

4)

5) , (2.27)

где 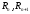- гидравлические радиусы, соответствующие соседним глубинам;

6) ,

где n_a – коэффициент шероховатости с учётом аэрации потока;

7) ,; (2.28)

где - коэффициенты Шези соседним глубинам

8) 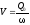, (2.29)

где - заданный расход воды, поступающий из подводящего канала;

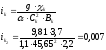
9) , (2.30)

где 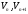- средние скорости в соседних сечениях;

10) ; (2.31)