Основные свойства определенного интеграла

1. Определенный интеграл с равными пределами равен нулю:

.

2. При перемене местами пределов интегрирования величина определенного интеграла изменяется на противоположную:

.

3. Если отрезок интегрирования разделен на конечное числоn частичных отрезков , то определенный интеграл от функциина отрезкеравен сумме определенных интегралов от этой функции на каждом из частичных отрезков (свойство аддитивности):

.

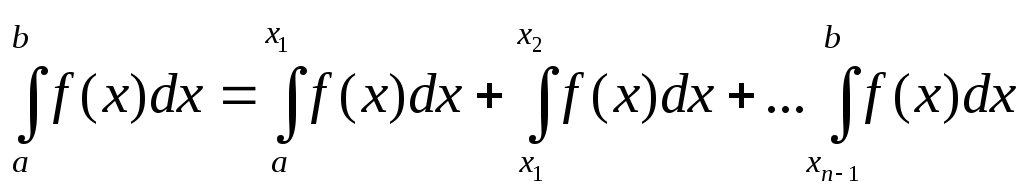4. ,

где - постоянный множитель.

5. Определенный интеграл от алгебраической суммы конечного числа функций, интегрируемых на отрезке , равен алгебраической сумме определенных интегралов этих функций на данном отрезке:

.

Величина определенного интеграла от функции , непрерывной на отрезке, равна приращению любой из первообразных для этой функции на данном отрезке:

, (23)

Формула (23) называется формулой Ньютона-Лейбница.

Из этой формулы следует, что для вычисления определенного интеграла достаточно найти какую-либо из первообразных для подынтегральной функции и из ее значения, соответствующего верхнему пределу интегрирования, вычесть значение, соответствующее нижнему пределу.

Пример 9. Вычислить определенный интеграл .

Решение. Первообразной для функции (имеющей наиболее простой вид), является. Поэтому в соответствии с формулой Ньютона-Лейбница имеем.

10. Основные методы вычисления определенных интегралов Метод разложения (непосредственного интегрирования)

Этот метод основан на использовании свойств определенного интеграла, знании формул простейших неопределенных интегралов и применении формулы Ньютона-Лейбница.

Пример 10. Вычислить определенный интеграл .

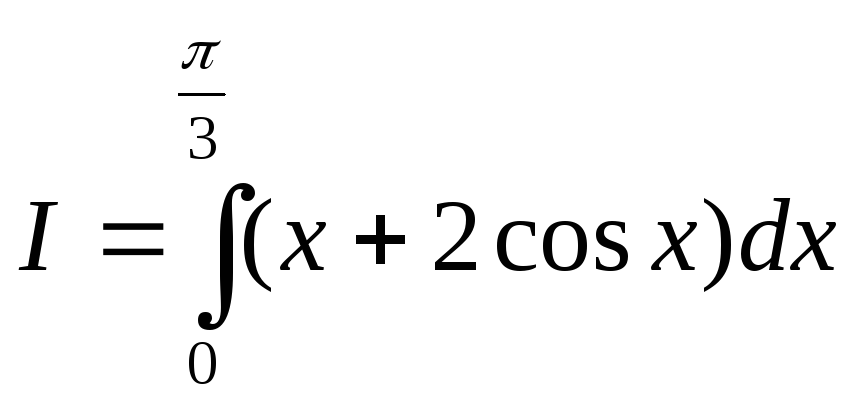Решение. Воспользуемся свойствами (3) и (4) определенных интегралов:

.

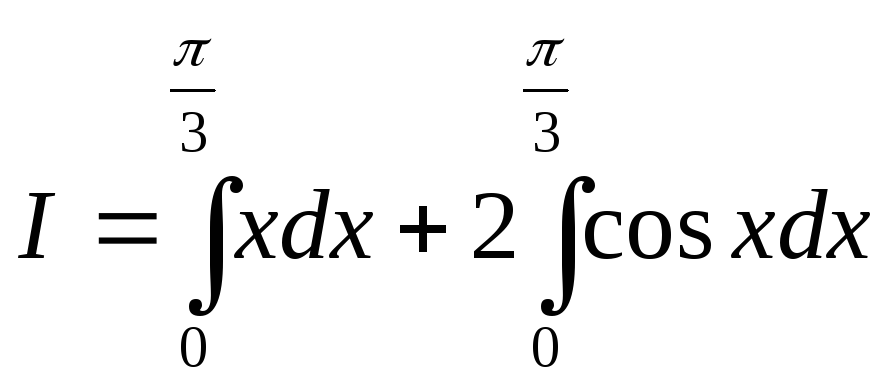Первообразные для подынтегральных функций найдем с помощью формул простейших определенных интегралов. Далее, используя формулу Ньютона-Лейбница, получим

.

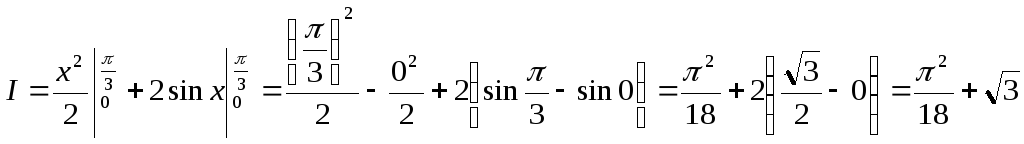Метод замены переменной (метод подстановки)

Этот метод основан на замене переменной интегрирования в определенном интеграле с целью свести его вычисление к вычислению такого определенного интеграла, который может быть вычислен методом разложения.

Пример 11. Вычислить интеграл .

Решение. Введем новую переменную ; Тогда, откуда.

При замене переменной интегрирования в определенном интеграле необходимо одновременно заменить пределы интегрирования на соответствующие . Имеем: при , при. Отсюда следует, что новым нижним пределом интегрирования будет значение 2, а новым верхним – значение 6. Таким образом

.

Замечание. Если при замене переменной в неопределенном интеграле мы от новой переменной возвращались к первоначальной переменной, то при замене переменной в определенном интеграле в этом нет необходимости.