
Задание 3 Циклические алгоритмы
.pdf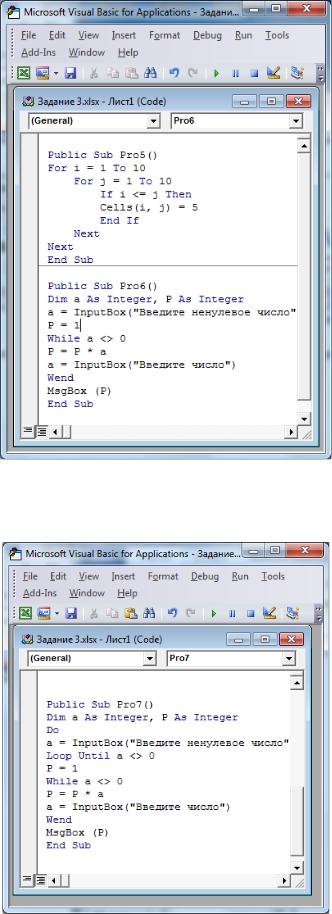
Задание №3. Циклические алгоритмы
1.Запустите редактор VBA и создайте процедуры, иллюстрирующие работу с циклами.
2.Выясните смысл процедуры. В чем отличие от предыдущей процедуры?

Задачи для самостоятельного решения
1.Найти наибольшее целое n такое, что
1)3n4 730n 5 ;
2)en 1000ln n 10 .
2. Дано целое число m 1. Получить наибольшее целое k, при котором
4k m .
3.Дано натуральное число n. Получить наименьшее число вида 2r , превосходящее n.
4.Числа Фибоначчи определяются формулами:
f0 f1 1; fn fn 1 fn 2 , |
n 2,3, . |
1)Найти f - первое число Фибоначчи, большее m (m>1);
2)вычислить s - сумму всех чисел Фибоначчи, которые не превосходят
1000.
5.Вычислить бесконечную сумму с заданной точностью 0.
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
1) |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
( 1) |
|
|
; |
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
i 1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
i! |
|
|
|
|
|
|
|
|
|
|
||||||
2) |
|
1 |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
4) ( 2) |
. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|||||
|
i 1 i(i 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
i! |
|
|
|
|
|
|
|
|
|
|
||||||||||
6. Составить |
программы |
вычисления |
значений функций с помощью |
||||||||||||||||||||||||||||||||||||
разложений в ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
k |
||||||
1) |
ln(1 x) x |
|
|
|
|
|
|
|
( 1)k 1 |
|
|
, |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
k |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2n 1 |
||||||||
2) |
sin x x |
|
|
|
|
|
|
|
( 1)2n 1 |
|
|
|
|
|
|
, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
3! |
|
|
|
|
|
5! |
|
|
|
|
|
n 1 |
|
|
(2n 1)! |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
x |
2n |
|
|
|
|
|||||||||||
3) |
cos x 1 |
|
|
|
|
|
|
|
( 1)n |
|
|
|
|
|
|
, |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
2! |
|
|
|
|
|
4! |
|
|
|
|
|
n 0 |
|
(2n)! |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4) |
ex 1 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
1! |
|
|
|
2! |
|
|
|
|
|
|
|
|
n 0 |
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Вычислять с точностью до члена ряда, меньшего . Сравнить с табличными значениями функций.

7.Задано действительное число a. Среди чисел вида: 1; 1 12 ; 1 12 13 ;...
найти первое, большее а.
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
8. |
Найти |
|
предел последовательности |
|
{yk }, если |
y0 2(2 2), |
||||||||||||||
|
y |
|
3 |
y |
|
1 |
xy3 , (число x -задано) |
с точностью . |
|
|
|
|||||||||
|
2 |
|
|
|
|
|||||||||||||||
|
n 1 |
|
n |
2 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9. |
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x 1; |
x |
2 x3 |
|
i 1,2,... |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
i 1 |
|
; |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
i |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
10 5 . |
|
|
|
||||||||||||
|
Найти первый член x |
, для которого |
x |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
n 1 |
|
|
|
|
||
10. Дано натуральное число n.
1)Сколько цифр в этом числе?
2)Чему равна сума его цифр?
3)Чему равно произведение его цифр?
4)Определить максимальную и минимальную цифру этого числа.
5)Определить первую и последнюю цифру этого числа.
6)Определить цифры, которых нет в этом числе.
7)Выяснить, входит ли цифра 3 в запись числа n.
8)Поменять порядок цифр числа n на обратный.
9)Переставить первую и последнюю цифры числа n.
10)Сколько раз входит 0 |
в запись этого числа? |
11)Проверить, будет ли сумма квадратов цифр, составляющих это число, |
|
больше самого числа. |
|
12)Определить количество различных цифр этого числа. |
|
13)Определить цифры, повторяющиеся в числе ровно М раз. |
|
14)Определить цифры, встречающиеся в n наиболее часто. |
|
11. Заданы числа x , h , |
n (n - целое). Определить количество и |
|
просуммировать т.е. |
члены |
последовательности: cos x, |
cos(x h), |
||||
|
cos(x 2h), ...,cos(x nh), которые по абсолютной величине меньше 0,5. |
|||||||
12. |
Заданы |
|
числа a, |
b, h. |
Вычислить |
сумму значений |
функции |
|
|
|
|
|
|
|
|
||
|
f (x) |
1 2x 3x3 |
для x , принадлежащих отрезку |
[a,b] и |
||||
|
изменяющихся с шагом h . |
|
|
|
||||
13. |
Вычислить значения многочлена 2a5 2a2 |
1.7a 12 для а=0, 1.5, 3, 4.5, |
||||||
|
6, 7.5, 9, 10.5. |
|
|
|
|
|
||

14. |
Вычислить последовательность значений функции y |
3x 2 |
2 |
для |
|
4 |
|||||
|
|
|
|||
|
значений аргумента х=0, 0.05, 0.1, …, 10. |
|
|
|
|
1. |
Даны целые числа n , k (n k 0) . Вычислить |
|
|
|
|
n(n 1)...(n k 1)
k! |
. |
16 Пусть n |
- натуральное число и пусть n!! означает 1 3 5 ... n для |
нечетного n и 2 4 6 ... n для четного n . Для заданного натурального n вычислить
1)n!!;
2)(1)n 1 n!!.
17.Вычислить:
100 |
1 |
|
50 |
|
|
1 |
|
|
|
|
|
|
|
|
10 |
|
1 |
|
|
|
|
|
|
|
|
128 |
1 |
|
|
|||||
1) |
; |
2) |
; |
|
|
|
|
3) |
; |
|
|
|
|
4) |
|
. |
||||||||||||||||||
2 |
3 |
|
|
|
|
|
(2i) |
2 |
||||||||||||||||||||||||||
i 1 |
i |
|
|
i 1 |
|
|
i |
|
|
|
|
|
|
i 1 |
i! |
|
i 1 |
|
|
|||||||||||||||
18. Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
5 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
101 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
19. Дано действительное число x 0. Вычислить |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
x2 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
256 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103 |
|
|
|
|
|
|
|
|
|||||||||
|
|
b |
|
|
|
1.8 |
|
|
|
|
|
|
ex |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
20. Вычислить |
S f (x)dx |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
по формуле правых |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
1 |
x |
0.4x |
2 |
|
|
|||||||||||||||||||||||||||||
|
|
a |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
прямоугольников с разбиением на N частей:

|
|
|
N |
|
|
|
|
b a |
|
|
|
|
|
|
|
|
|
|
S h f (xi ), |
|
|
h |
, |
xi a ih. |
|||||||||
|
|
|
|
|||||||||||||
|
|
|
i1 |
|
|
|
|
N |
|
|
|
|
|
|
||
|
|
b |
1.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
21. |
Вычислить |
S f (x)dx |
1 x2 0.4sin xdx |
по формуле левых |
||||||||||||
|
|
a |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямоугольников с разбиением на N частей: |
|
|
|
||||||||||||
|
|
|
N 1 |
|
|
|
|
b a |
|
|
|
|
|
|
|
|
|
|
S h f (xi ), |
|
|
h |
, |
xi a ih. |
|||||||||
|
|
|
|
|
||||||||||||
|
|
|
i0 |
|
|
|
|
N |
|
|
|
|
|
|
||
|
|
b |
1.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
20. |
Вычислить |
S f (x)dx lg |
|
1 0.2x x2 dx по |
|
формуле срединных |
||||||||||
|
|
a |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямоугольников с разбиением на N частей: |
|
|
|
||||||||||||
|
|
|
N |
|
|
|
b a |
|
|
|
|
|
|
h |
|
|
|
|
S h f (xi ), h |
, xi |
a ih |
. |
|||||||||||
|
|
|
|
|||||||||||||
|
|
|
i1 |
|
|
|
N |
|
|
|
2 |
|
||||
