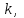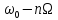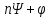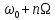Некоммерческое акционерное общество
«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ »
Кафедра телекоммуникационных систем
КУРСОВАЯ РАБОТА
по дисциплине: Теория электрической связи
На тему «Амплитудная, частотная модуляции»
Специальность:050719 Радиотехника, электроника и телекоммуникации.
Выполнила: Нурдильдаулы Б. Группа: БРЭ-10-13 № зач.кн. 103232
Руководитель: Богомолова Л.Г.
Алматы,2012
Содержание
Введение...................................................................................................................3
Задача№1..................................................................................................................4
Задача№2................................................................................................................14
Заключение……………….....................................................................................23
Список использованной литературы…………………………………………...24

Введение
Данная курсовая работа предусматривает изучение различных видов модуляции: амплитудной, фазовой, частотной, импульсной. При выполнении этой работы необходимы знания принципов работы составных элементов системы связи: модулятора и демодулятора, АЦП и ЦАП, кодера и декодера.
Существуют три основные схемы модуляции: 1) амплитудная модуляция(AM); 2) угловая модуляция, подразделяющаяся на два очень похожих метода: частотную модуляцию (ЧМ) и фазовую модуляцию (ФМ); 3) импульсная модуляция (ИМ). Различные схемы модуляции совмещают два этих метода или более, образуя сложные системы связи. Телевидение, например, использует как AM, так и ЧМ для различных типов передаваемой информации. Импульсная модуляция совмещается с амплитудной, образуя импульсно-амплитудную модуляцию (АИМ), и т.д. Не всегда возможно найти четко выраженные основания для использования того или иного метода модуляции. В некоторых случаях этот выбор предписывается законом (в США контроль осуществляет Федеральная комиссия по связи — ФКС). Необходимо строго придерживаться правил и инструкций независимо от того, какая схема модуляции используется.
Задача оптимизации систем передачи информации сводится к нахождению наилучшего варианта системы при заданных условиях и ограничениях, при котором потребителю в единицу времени доставляется максимальное количество информации при заданной верности передачи. Для повышения эффективности систем используются сокращение избыточности источника, помехоустойчивое кодирование и др.

Задача 1
Заданы: несущее колебание
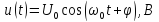 (1.1)
(1.1)
модулирующий сигнал
 (1.2)
(1.2)
где
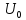 - амплитуда несущего колебания;
- амплитуда несущего колебания;
 – частота несущего колебания;
– частота несущего колебания;
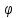 – начальная фаза несущего колебания;
– начальная фаза несущего колебания;
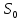 – амплитуда модулирующего колебания;
– амплитуда модулирующего колебания;
 –
частота модулирующего колебания;
–
частота модулирующего колебания;
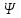 – начальная фаза модулирующего колебания.
– начальная фаза модулирующего колебания.
Требуется:
а)
в соответствии с вариантом записать
аналитическое выражение
амплитудно-модулированного колебания
с коэффициентом глубины модуляции М;
частотно-модулированного колебания с
девиацией частоты
 ;
фазо-модулированного колебания с
индексом модуляцииm.
;
фазо-модулированного колебания с
индексом модуляцииm.
б) колебаний изобразить качественно графики модулирующего и модулированного сигналов АМ, ЧМ, ФМ (временные диаграммы колебаний);
в) построить амплитудно-частотный и фазо-частотный спектры АМ, ЧМ и ФМ колебаний.
Исходные данные (см. таблица 1.2 и 1.3) выбираем по номеру зачетной книжки.
Исходные данные
Таблица 1 – Исходные данные к задаче 1
|
|
1,5 |
|
|
3,6 |
|
|
|
|
|
0,5 |
|
|
0,8 |
|
|
|
|
|
1,3 |
|
m |
2 |
|
Глубина
модуляции
|
65 |
Решение задачи 1
а) Рассчитаем частоты несущего и модулирующего колебаний:
 рад/с
рад/с
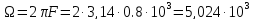 рад/с
рад/с
Несущее колебание
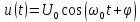

Модулирующий сигнал
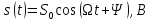
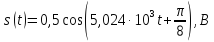
Коэффициент модуляции

Аналитическое выражение для мгновенных значений тонально-модулированных колебаний в общем случае имеет вид
АМК:
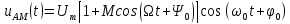
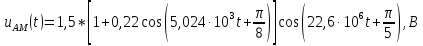 (1)
(1)
ФМК:
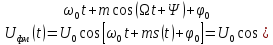 )
)
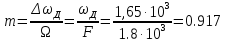
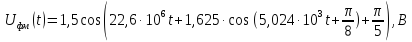 (2)
(2)
ЧМК:

 ,
В (3)
,
В (3)
б) изобразить качественно графики модулирующего и модулированного сигналов АМ, ЧМ, ФМ (временные диаграммы колебаний);
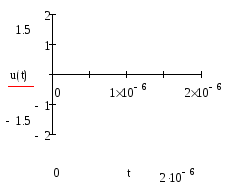
Рисунок 1.1а

Рисунок 1.1б
Рисунок 1.1а - Временная диаграмма модулирующего сигнала; Рисунок 1.1б - Временная диаграмма несущей.
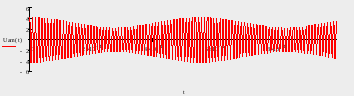
Рисунок 1.2 - Временная диаграмма колебаний модулируемого сигнала АМ

Рисунок 1.3 - Временная диаграмма колебаний модулируемого сигнала ФМ

Рисунок 1.4 - Временная диаграмма колебаний модулируемого сигнала ЧМ
в) построить амплитудно-частотный и фазо-частотный спектры АМ, ЧМ и ФМ колебаний.
Для построения спектров аналитические выражения (1), (2) и (3) следует представить в развернутом виде.
для АМ:

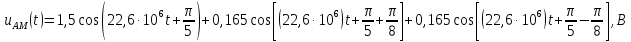
АЧ и ФЧ спектры АМК, построенные в MathCad 14, будут выглядеть следующим образом (рисунки 1.5 и 1.6):
![]()
![]()
![]()
![]()
![]()
![]()

Рисунок 1.5 – График АЧ спектра АМ колебания
![]()
![]()
![]()
![]()
![]()
![]()

Рисунок 1.6 – График ФЧ спектра АМ колебания
Для фазовой модуляции воспользуемся соотношениями функций Бесселя и получим:
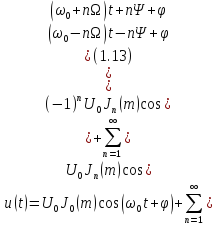
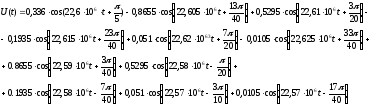
где Jn(m) – функция Бесселя первого рода порядка n с индексом модуляции m в качестве аргумента. Значение функций Бесселя для разных n и m=2 приведены в таблице 2, а также амплитуды и фазы.
Таблица2 - Функции Бесселя для m=6, амплитуды и фазы
|
N |
Jn(2) |
|U0*Jn(2)|, B |
|
|
|
|
|
0 |
0,224 |
0.336 |
22600 |
22600 |
π/5 |
π/5 |
|
1 |
0,577 |
0.8655 |
22605 |
22595 |
13π/40 |
3π/40 |
|
2 |
0,353 |
0.53 |
22610 |
22580 |
18π/40 |
-2π/40 |
|
3 |
0,129 |
0.19 |
22615 |
22585 |
23π/40 |
-7π/40 |
|
4 |
0,034 |
0.051 |
22620 |
22580 |
24π/40 |
-12π/40 |
|
5 |
0,007 |
0,01 |
22625 |
22575 |
33π/40 |
-17π/40 |
АЧ и ФЧ спектры ФМК, построенные в MathCad 14, будут выглядеть следующим образом (рисунки 1.7 и 1.8):
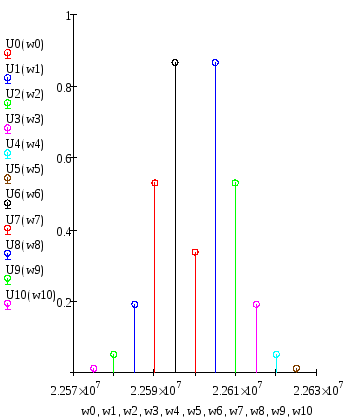
Рисунок 1.7 – График АЧ спектра ФМ колебания
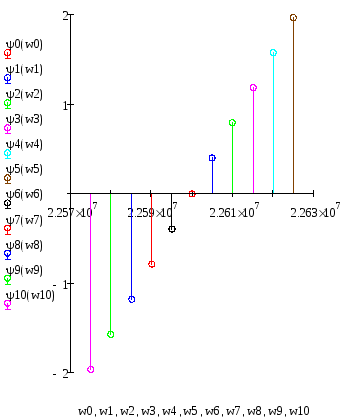
Рисунок 1.8 – График ФЧ спектра ФМ колебания
Для получения аналитического выражения ЧМ-колебания вычислили индекс угловой модуляции m, равный 0.146. Воспользуемся соотношениями функций Бесселя и получим:
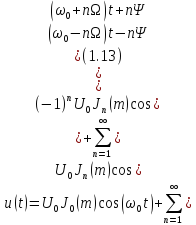
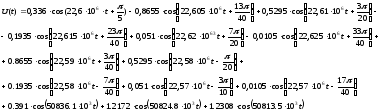
где Jn(m) – функция Бесселя первого рода порядка n с индексом модуляции m в качестве аргумента. Значение функций Бесселя для разных n и m=2 приведены в таблице 2, а также амплитуды и фазы.
Таблица2 - Функции Бесселя для m=6, амплитуды и фазы
|
N |
Jn(2) |
|U0*Jn(2)|, B |
|
|
|
|
|
0 |
0,224 |
0.336 |
22600 |
22600 |
0 |
0 |
|
1 |
0,577 |
0.8655 |
22605 |
22595 |
π/8 |
-π/8 |
|
2 |
0,353 |
0.53 |
22610 |
22580 |
2π/8 |
-2π/8 |
|
3 |
0,129 |
0.19 |
22615 |
22585 |
3π/8 |
-3π/8 |
|
4 |
0,034 |
0.051 |
22620 |
22580 |
4π/8 |
-4π/8 |
|
5 |
0,007 |
0,01 |
22625 |
22575 |
5π/8 |
-5π/8 |
АЧ и ФЧ спектры ЧМК, построенные в MathCad 14, будут выглядеть следующим образом (рисунки 1.9 и 1.10):

Рисунок 1.9 – График АЧ спектра ЧМ колебания
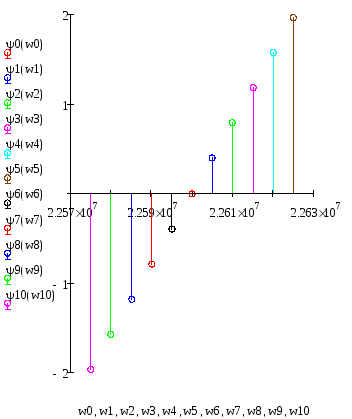
Рисунок 1.10 – График ФЧ спектра ЧМ колебания

 ,
В
,
В ,
МГц
,
МГц
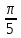
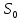 ,
В
,
В ,
кГц
,
кГц ,
рад
,
рад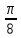
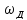 ,
кГц
,
кГц