Matem_2_Komp_test

D)

@183

Действительная часть комплексного числа равна:

183@

A)

B)

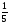
C)

D)

@184

Действительная часть комплексного числа равна:

184@

A)

B)

C) 2

D)

@185

Мнимая часть комплексного числа равна:

185@

A)

B)

C)

D)

@186

Мнимая часть комплексного числа равна:

186@

A)

B)

C)

D)

@187

Мнимая часть комплексного числа равна:

187@

A)

B)

C)

D)

@188

Мнимая часть комплексного числа равна:

188@

A)

B)

C)

D)

@189

равен:

189@

A)

B)

C)

D)

@190

равен:

190@

A)

B)

C)

D)

@191

равен:

191@

A)

B)

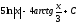
C)

D)

@192

равен:

192@

A)

B)

C)

D)

@193

Внести под знак дифференциала

193@

A)

B)

C)

D)

@194

Внести под знак дифференциала :

194@

A)

B)

C)

D)

@195

Внести под знак дифференциала

195@

A)

B)

C)

D)

@196

Внести под знак дифференциала

196@

A)

B)

C)

D)

@197

Вынести из-под знака дифференциала

197@

A)

B)

C)

D)

@198

Вынести из-под знака дифференциала

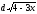
198@

A)

B)

C)

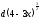
D)

@199

Вынести из-под знака дифференциала

199@

A)

B)

C)

D)

@200

Вынести из под знака дифференциала

200@

A)

B)

C)

D)

@201

Повторный интеграл равен:

201@

A)

B)

C)

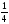
D)

@202

Повторный интеграл равен:

202@

A)

B)

C)

D)

@203

Повторный интеграл равен:

203@

A)

B)

C)

D)

@204

Повторный интеграл равен:

204@

A)

B)

C)

D)

@205

Повторный интеграл равен:

205@

A)

B)

C)

D)

@206

Повторный интеграл равен:

206@

A)

B)

C)

D)

@207

Повторный интеграл равен:

207@

A)

B)

C)

D)

@208

Повторный интеграл равен:

208@

A)

B)

C)

D)

@209

Повторный интеграл равен:

209@

A)

B)

C)

D)

@210

Повторный интеграл равен:

210@

A)

B)

C)

D)

@211

Повторный интеграл, к которому сводится двойной интеграл есть:

211@

A)

B)

C)

D)

@212

Повторный интеграл, к которому сводится двойной интеграл ,

есть:

212@

A)

B)

C)

D) п.о.н

@213

Повторный интеграл, к которому сводится двойной интеграл есть:

213@

A)

B)

C)

D)

@214

Повторный интеграл, к которому сводится двойной интеграл есть:

214@

A)

B)

C)

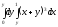
D)

@215

Якобиан преобразования в двойном интеграле равен:

215@

A)

B)

C)

D)

@216

Якобиан преобразования в двойном интеграле равен:

216@

A)

B)

C)

D)

@217

Якобиан преобразования в двойном интеграле равен:

217@

A)

B)

C)

D)

@218

Якобиан преобразования в двойном интеграле равен:

218@

A)

B)

C)

D)

@219

Якобиан преобразования в двойном интеграле равен:

219@

A)

B)

C)

D) -1

@220

Якобиан преобразования в двойном интеграле равен:

220@

A)

B)

C)

D)

@221

Якобиан преобразования в двойном интеграле равен:

221@

A)

B)

C)

D)

@222

после замены , есть:

222@

A)

B)

C)

D)

@223

после замены, есть:

223@

A)

B)

C)

D)

@224

после замены есть:

224@

A)

B)

C)

D)

@225

после замены есть:

225@

A)

B)

C)

D)

@226

после замены есть

226@

A)

B)

C)

D)

@227

после замены есть:

227@

A)

B)

C)

D)

@228

после замены есть:

228@

A)

B)

C)

D)

@229

после замены есть:

229@

A)

B)

C)

D)

@230

, после замены есть:

230@

A)

B)

C)

D)

@231

Повторный интеграл, к которому сводится тройной интеграл есть:

231@

A)

B)

C)

D)

@232

Повторный интеграл, к которому сводится тройной интеграл есть:

232@

A)

B)

C)

D)

@233

Повторный интеграл, к которому сводится тройной интеграл есть:

233@

A)

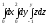
B)

C)

D)

@234

Повторный интеграл, к которому сводится тройной интеграл есть:

234@

A)

B)

C)

D)

@235

Повторный интеграл, к которому сводится тройной интеграл есть:

235@

A)

B)

C)

D)

@236

равен:

236@

A)

B)

C)

D)

@237

равен:

237@

A)

B)

C)

D)

@238

равен:

238@

A)

B)

C)

D)

@239

равен:

239@

A)

B)

C)

D)

@240

равен:

240@

A)

B)

C)

D)

@241

Объем тела равен:

241@

A)

B)

C)

D)

@242

Объем тела равен:

242@

A)

B)

C)

D)

@243

Объем тела равен:

243@

A)

B)

C)

D)

@244

Объем тела равен:

244@

A)

B)

C)

D)

@245

Объем тела равен:

245@

A)

B)

C)

D)

@246

Объем тела 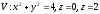равен:

246@

A)

B)

C)

D)

@247

Объем тела равен:

247@

A)

B)

C)

D)

@248

Объем тела равен:

248@

A)

B)

C)

D)

@249

Объем тела равен:

249@

A)

B)

C)

D)

@250

Объем тела равен:

250@

A)

B)

C)

D)

@251

Поверхностный интеграл по поверхности S; где - часть плоскости отсеченная координатными плоскостями , приводится к двойному:

251@

A)

B)

C)

D)

@252

Поверхностный интеграл по поверхности S; где - часть плоскости отсеченная координатными плоскостями , приводится к двойному:

252@

A)

B)

C)

D)

@253

Поверхностный интеграл по поверхности S; где - часть плоскости отсеченная координатными плоскостями , приводится к двойному:

253@

A)

B)

C)

D)

@254

Поверхностный интеграл по поверхности S; где - часть плоскости отсеченная координатными плоскостями , приводится к двойному:

254@

A)

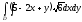
B)

C)

D) п.o.н.

@255

Поверхностный интеграл по поверхности S; где - часть плоскости отсеченная координатными плоскостями , приводится к двойному:

255@

A)

B)

C)

D) п.о.н.

@256

Криволинейный интеграл первого рода , где - отрезок прямой от точки до точки, приводится к определенному интегралу вида:

256@

A)

B)

C)

D)

@257

Криволинейный интеграл первого рода , где - отрезок прямой от точки до точки, приводится к определенному интегралу вида:

257@

A)

B)

C)

D)

@258

Криволинейный интеграл первого рода 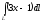, где- отрезок прямой от точки до точки, приводится к определенному интегралу вида:

258@

A)

B)

C)

D)

@259

Криволинейный интеграл первого рода , где L - отрезок прямой от точки до точки, приводится к определенному интегралу вида:

259@

A)

B)

C)

D)

@260

Криволинейный интеграл первого рода , где - отрезок прямой от точки до точки, приводится к определенному интегралу вида:

260@

A)

B)

C)

D)

@261

Криволинейный интеграл второго рода , где - отрезок прямой от точки до точки , в виде определенного интеграла есть:

261@

A)

B)

C)

D)

@262

Криволинейный интеграл второго рода где - отрезок прямой первая арка циклоиды, в виде определенного интеграла есть:

262@

A)

B)

C)

D)

@263

Криволинейный интеграл второго рода где отрезок прямой первая арка циклоиды, в виде определенного интеграла есть:

263@

A)

B)

C)

D)

@264

Криволинейный интеграл второго рода , где дуга параболы от точки до точки , в виде определенного интеграла есть:

264@

A)

B)

C)

D)

@265

Криволинейный интеграл второго рода , где - верхняя половина эллипса , в виде определенного интеграла есть:

265@

A)

B)

C)

D)

@266

Криволинейный интеграл второго рода по замкнутому контуру в виде двойного интеграла по формуле Грина есть:

266@

A)

B)

C)

D)

@267

Криволинейный интеграл второго рода по формуле Грина приводится к двойному интегралу вида: