lab1

Алматинский университет энергетики и связи

Кафедра ТОЭ

ОТЧЕТ по лабораторной работе №1

Исследование цепей постоянного тока

Работа выполнена: 17.09.13

Студентом: Кужагулов М.Б.

Группа: АУ-12-6

Совместно со студентами:

Тен А.

Умирзакова А.

Ельтиндинова Ж.

Отчет принят:

Преподаватель:ст. преп. Креслина С.Ю.

Алматы 2013

Лабораторная работа №1. Исследование цепей постоянного тока

Цель работы: Получение навыков экспериментального исследования цепей постоянного тока.

Подготовка к работе

Письменно ответить на следующие вопросы:

1. Привести формулировки законов Ома и Кирхгофа.

Закон Ома – сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна его сопротивлению.

Законы Кирхгофа

1-ый закон: алгебраическая сумма токов. Сходящихся в узле электрической цепи, равна нулю.

2-ой закон: в любом замкнутом контуре алгебраическая сумма падений напряжений на резистивных элементах равна алгебраической сумме ЭДС.

2. Каковы особенности применения законов Кирхгофа при анализе цепей с источниками тока?

Правила Кирхгофа имеют прикладной характер и позволяют решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами для расчета разветленных цепей, т.е. для определения тока на любом участке цепи, и для определения напряжения в любой точке цепи.

3. Какой источник энергии называется источником напряжения (ЭДС) и какой источником тока? Привести электрические схемы реальных и идеальных источников напряжения и тока.

Источником напряжения, у которого внутреннее сопративление равно нулю. Источником тока называется источник постоянного или переменного тока, у которого внутреннее сопротивление равно бесконечности.

4. В чем суть принципа наложения?

Суть этого метода состоит в том, что в сложной схеме с несколькими источника последовательно рассчитываются частные токи от каждого источника в отдельности, оставляя в схеме по одной э.д.с., считая все остальные э.д.с. источники равными нулю, но при этом сохраняя в схеме их внутреннее сопротивление.

5. Как записать ток в какой-либо ветви при помощи ЭДС источников и входных, и взаимных проводимостей ветвей?

Входная проводимость любой ветви определяется отношением тока к э.д.с. в этой ветви при равных нулю э.д.с. в остальных ветвях, а входное сопротивление ветви обратно входной проводимости.

Взаимная проводимость двух любых ветвей определяется отношением тока в одной ветви к э.д.с. в другой при равных нулю э.д.с. в остальных ветвях, а взаимное сопротивление двух ветвей обратно взаимной проводимости тех же ветвей.

6. Что такое потенциальная диаграмма цепи?

Распределение потенциала вдоль неразветвленной электрической цепи можно наглядно представить при помощи графика, который называют потенциальной диаграммой.

7. Привести формулы расчета эквивалентного сопротивления при последовательном, параллельном, смешанном соединении сопротивлений, а также формулы преобразования треугольника сопротивлений в эквивалентную звезду сопротивлений и наоборот.

1.При последовательном соединении n резисторов с сопротивлением R1, R2, ..Rn, эквивалентное сопротивление равно сумме сопротивлений этих резисторов:  Rэ = R1+R2+...+Rn 

2. При параллельном соединении n резисторов с сопротивлением R1, R2, ..Rn, эквивалентное сопротивление цепи вычисляется из формулы:  1/Rэ = 1/R1 + 1/R2 +..+1/Rn

На рис. 2.9 а между точками 1, 2 и 3 некоторой сложной цепи включены три участка с сопротивлениями Z₁, Z₂ и Z₃, соединенные звездой.

Решая эти уравнения относительно токов и , получим:

  

где

D=Z₁Z₂+Z₂Z₃+Z₃Z₁.

Для соединения треугольником имеем уравнения:

    

Например, формула для Z₁ получается, если заметить, что

  и  

При эквивалентном преобразовании треугольника в звезду и наоборот возможны случаи, когда

Упрощение расчета сложной цепи при помощи эквивалентного преобразования конфигурации цепи можно проследить на примере расчета цепи, изображенной на рис. 2.10 а.

Рис. 2.10. Упрощение расчета сложной цепи при помощи эквивалентного преобразования конфигурации цепи

В этой цепи упрощение достигается преобразованием треугольника Z₁₂, Z₂₃, Z₃₁ (рис. 2.10 а) в эквивалентную звезду Z₁, Z₂, Z_З (рис. 2.10 б). После такого преобразования получаем простую цепь с последовательно-параллельным соединением участков.

Порядок выполнения работы

2. Измерить сопротивления всех резисторов, заполнить таблицу 1.1

Таблица 1.1

Резистор
Oм	75,3	526,3	285	200	1014	821

Согласно варианту задания, рисунок 1, изобразить исследуемую схему, задаться положительными направлениями токов в ветвях. Собрать цепь из резисторов, и источников напряжения. При сборке предусмотреть клеммы для подключения измерительных приборов. Ампервольтметры подключить в соответствии с выбранными направлениями токов.

Рисунок 1

3. Токи в ветвях.

Таблица 1.2

33,98	23,8	10,8	33,25	9,15	1,6

4. Принять условно потенциал одного из узлов за нуль. Измерить потенциалы всех точек, указанных на схеме. Результаты занести в таблицу 1.3.

Таблица 1.3

,	,	,	,	,	,
0	-19,53	-16,23	-6,82	-22,19	-1,6

4. Оформление и анализ результатов работы

4.1. Проверить выполнение 1 закона Кирхгофа для цепи. Рассчитать для каждого узла погрешность измерения токов.

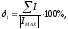
где - наибольший из токов данного узла. Результат занесен в таблицу 1.5

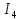+ – = 0

1,6 +33,25 –33,98 = 0,87

*100 = 2,56 < 5%

+ – = 0

10,8 + 23,8 – 33,98 = 0,62

*100 = 1,82 < 5%

+ – = 0

1,6 + 9,15 – 10,8 =0,05

*100 = 0,4 < 5%

4.2 Проверить выполнение второго закона Кирхгофа для цепи. Рассчитать для каждого контура погрешность измерения напряжений.

где - наибольшее из напряжений данного контура. Результаты занести в таблицу 1.6.

= 21,9

++=

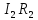33,98*75,3 + 33,25*200 + 23,8*526,3= =21,7

= 21,9 - 21,7 = 0,2

= 14,61

+=

33,25*200 + 9,15*1014 – 1,6*821 = = 14,6

= 14,61 – 14,6 = 0,01

Е= 0

++=

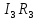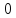
–23,8*526,3 + 9,15* 1014 +10,8* 285 = = -0,17

= 0,17 – 0 = 0,17

Таблица 1.5

Узлы		1	2	3
Сумма токов	мA	0,87	0,62	0,05
Максимальный ток в узле	мА	33,98	33,98	10,8
Погрешность	%	2,56	2	0,4

Таблица 1.6

Контуры		1	2	3
Сумма напряжений	В	21,7	14,61	-0,17
Максимальное напряжение в контуре	В	12518	6796	9278,1
Погрешность	%	0,2	0,01	0,17

5. Построить потенциальную диаграмму для внешнего контура исследуемой цепи

6. Выводы о проделанной работе.

Результаты проведенных исследований цепи постоянного тока показывают экспериментальное подтверждение расчетных методов . Отличия результатов эксперимента и расчетные значения лежат в допустимых пределах (не превышают 5 %) и объясняются погрешностью измерения токов и напряжений, разбросом параметров сопротивлений.
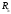
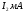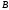
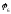