Некоммерческое акционерное общество

«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»

Кафедра «Электрические станции, сети и системы»

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 3

По дисциплине: «Электротехническое материаловедение»

Специальность: 5B071800 Электроэнергетика

Выполнил: Ибатаев Данияр Группа: Э-13-9

№ зачетной книжки – 124381

Руководитель: доцент, Оспанова Г.Ж.

Алматы 2015

Содержание:

Задача 1 3

Задача 2 5

Заключение 6

Список использованной литературы 7

Задача 1

К диэлектрику прямоугольной формы размерами а·b и высотой h приложено постоянное напряжение U = 1000 В. Напряжение подводится к противоположным граням аb, покрытым слоями металла. Известны размеры диэлектрика: а = 320 мм, b = 145 мм, h = 4 мм, удельное объемное сопротивление и удельное поверхностное сопротивление , =3,1 - относительная диэлектрическая проницаемость, тангенс угла диэлектрических потерь при 20.

1) Требуется определить ток утечки, мощность потерь и удельные диэлектрические потери.

2) Требуется определить мощность потерь и удельные диэлектрические потери температурах и при переменном напряжении U=1000 В и частоте f=100 Гц. Коэффициент, характеризующий температурную зависимость тангенса угла диэлектрических потерь,

Решение:

1. Ток утечки протекает как через объем диэлектрика, так и по поверхностям четырех боковых граней (через две грани a и через две грани b). Поэтому сопротивление между электродами определяется параллельным соединением объемного и поверхностного сопротивлений. Объемное сопротивление равно:

Поверхностное сопротивление равно:

Полное сопротивление изоляции равно:

Ток утечки:

Мощность потерь:

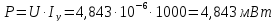
Удельные диэлектрические потери:

Определим емкость плоского конденсатора, образованного металлическими гранями, между которыми находится диэлектрик, полагая, что εr не зависит от температуры:

Мощность диэлектрических потерь при температуре 20°С будет равна:

Удельные диэлектрические потери при температуре 20°С:

Учтем, что тангенс дельта изменяется с температурой по экспоненциальному закону: Тогда мощность диэлектрических потерь при температуре 100°С будет равна:

Удельные диэлектрические потери при температуре 100°С:

Задача 2

Расстояние между плоскими токоведущими частями заполнено диэлектриком, имеющим значение относительной диэлектрической проницаемости и электрической прочности E_пр1 = 30 кВ/мм. Какое предельное напряжение можно приложить к токоведущим частям и насколько снизится это напряжение, если между токоведущими частями появится микротрещина – воздушная прослойка толщиной ? Электрическая прочность воздуха Е_пр2 = 3 кВ/мм, а относительная диэлектрическая проницаемость равна .

Решение:

Предельное напряжение между токоведущими частями при отсутствии микротрещин равно:

При наличии микротрещины – воздушной прослойки напряжение между токоведущими частями будет равно:

Зная, что напряженности в различных слоях обратно пропорциональны диэлектрическим проницаемостям, т.е:

Выразим напряженность E_пр1 в диэлектрике:

И подставим это значение в уравнение для напряжения:

Отсюда следует, что значение предельного напряжения уменьшилось в 17 раз, что, естественно, приведет к преждевременному пробою изоляции.

Заключение

Электротехнические материалы имеют существенное значение в конструкциях самых разнообразных электротехнических и радиотехнических устройств и аппаратов. Учитывая тенденцию в современной электротехнике к увеличению напряжений и мощностей, уменьшению габаритов и веса отдельных машин и аппаратов и повышению их надежности, роль электроматериалов становится более значительной.

Список использованной литературы

1.Богородитский Л.П., Пасынков В.В., Тареев Б.М, Электротехнические материалы. 2-е изд. – Л.: Энероатомиздат, 1985. -304 с.;

2.Корицкий Ю.В. Электротехнические материалы. 3-е изд.- М.:Высшая школа, 1990.-306 с.;

3.Конспект лекций по «Электротехническому материаловедению».