Регрессионный анализ

Смоленск 2009

Регрессией Y на X или условным математическим ожиданием случайной величины Y относительно случайной величины X называется функция вида

Регрессией X на Y называется функция вида

= φ(y).

Оценками этих функций являются выборочные уравнения регрессии, или условные средние,

= φ^*(y).

На практике часто используются выборочные уравнения линейной регрессии в виде

.

Для определения параметров ρ и β в уравнении используется получаемая на основании метода наименьших квадратов система двух уравнений

Аналогично находятся параметры ρ₁ и β₁ для функции

Для оценки связи между случайными величинами обычно используется выборочный коэффициент корреляции:

Выборочный коэффициент корреляции представляет собой отношение

.

В том случае, когда варианты парной выборки встречаются по нескольку раз, причём с одним значением варианты x_i может встретиться несколько вариант y_i, их обычно представляют в виде корреляционной таблицы. На пересечении строк и столбцов этой таблицы отмечается частота выбора соответствующей парыа частоты вариантнаходятся как суммы значенийпо соответствующей строке или столбцу. Например, в корреляционной таблице

xi yj	10	20	30
5	3	–	2	5
10	5	4	2	11
	8	4	4	n = 16

пара (10; 5) встречается 3 раза, т.е. а частота появления величинынаходится как сумма

Очевидно, что

Для коэффициента корреляции случайных величин X и Y в случае сгруппированных данных используется выражение

где

После подсчёта получают выборочное уравнение линейной регрессииY на X в виде

или выборочное уравнение линейной регрессии X на Y в виде

Для упрощения расчетов часто используются условные варианты, которые подсчитываются по формулам

где С₁, С₂ – ложные нули (выбираемые значения);

h₁, h₂ – разности между соседними значениями X и Y.

Соответственно, для обратного перехода применяются выражения

где – средние значения условных вариант;

средние квадратичные отклонения условных вариант.

Для подсчёта выборочного коэффициента корреляции в этом случае используются формула

где

Подсчитав выборочный коэффициент корреляции через условные варианты и осуществив переход к условным переменным, получают соответствующие уравнения регрессии.

Цель занятия: 1.Уяснить различие между функциональной и статистической зависимостью двух переменных.

2.Объяснить общую идею подбора эмпирических уравнений регрессии методом наименьших квадратов

К занятию по данной теме должны быть подготовлены следующие вопросы:

1.Что называется модельным уравнением регрессии Y на X?

2.Что называется эмпирическим уравнением регрессии Y на X? Пояснить его смысл.

3.Какие основные задачи корреляционного анализа и регрессионного анализа?

4.Какие критерии применяются для проверки гипотез относительно коэффициента корреляции генеральной совокупности?

Задача 1. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты X и числа уволившихся за год рабочих Y:

X	100	150	200	250	300
Y	60	35	20	20	15

Найти линейную регрессию X на Y и выборочный коэффициент корреляции.

Решение. Составим расчётную таблицу:

i	xi	yi
1	100	60	10000	6000	3600
2	150	35	22500	5250	1225
3	200	20	40000	4000	400
4	250	20	62500	5000	400
5	300	15	90000	4500	225
	1000	150	225000	24750	5850

Определяем ρ и β:

Выборочное уравнение регрессии примет вид

Из расчетной таблице следует, что

По формуле находим

Найдём по формулам

Откуда

Таким образом,

Задача 2. В магазине постельных принадлежностей в течение пяти дней подсчитывали число покупок простыней X и подушек Y:

xi	10	20	25	28	30
yi	4	8	7	12	14

(В данной таблице значения X расставлены в возрастающем порядке.) Найти выборочное уравнение линейной регрессии и выборочный коэффициент корреляции.

Решение. Составим таблицу подсчётов.

Номер опыта i
1 2 3 4 5	10 20 25 28 30	4 8 7 12 14	100 400 625 784 900	40 160 175 336 420	16 64 49 144 196
	113	45	2809	1131	469

Находим ρ и β:

Уравнение регрессии запишется в виде

Подсчитаем корреляционный момент:

Находим

Определим выборочную дисперсию величин X и Y:

Откуда

Задача 3. Найти выборочное уравнение линейной регрессии X на Y на основании корреляционной таблицы

xi yj	15	20	25	30	35	40
100	2	1	–	7	–	–
120	4	–	2	–	–	3
140	–	5	–	10	5	2
160	–	–	3	1	2	3

Решение. Для упрощения расчётов введём условные варианты

и составим преобразованную корреляционную таблицу с условными вариантами, в которую внесём значения и:

ui vj	-3	-2	-1	0	1	2
-1	2	1	–	7	–	–	10
0	4	–	2	–	–	3	9
1	–	5	–	10	5	2	22
2	–	–	3	1	2	3	9
	6	6	5	18	7	8	n=50

Затем составим новую таблицу, в которую внесём посчитанные значения в правый верхний угол заполненной клетки ив левый нижний угол, после чего суммируем верхние значения по строкам для получения значенийи нижние значения по столбцам дляи подсчитаем величиныи(табл.).

ui vj	-3	-2	-1	0	1	2
-1	-6 2 -2	-2 1 -1	–	0 7 -7	–	–	-8	8
0	-12 4 0	–	-2 2 0	–	–	6 3 0	-8	0
1	–	-10 5 5	–	0 10 10	5 5 5	4 2 2	-1	-1
2	–	–	-3 3 6	0 1 2	2 2 4	6 3 6	5	10
	-2	4	6	5	9	8	–
	6	-8	-6	0	9	16		–

Подсчитываем суммы иПараллельный подсчёт этих сумм осуществляется для контроля правильности расчетов. В данном случае

Находим и:

Находим :

Определяем :

Вычисляем выборочный коэффициент корреляции :

Осуществляем переход к исходным вариантам:

Находим уравнение регрессии X на Y:

или

Задача 4. Найти выборочное уравнение линейной регрессии Y на X на основании корреляционной таблицы.

yj	xi						ny
	10	20	30	40	50	60
15 25 35 45 55	5 – – – –	7 20 – – –	– 23 30 10 –	– – 47 11 9	– – 2 20 7	– – – 6 3	12 43 79 47 19
nx	5	27	63	67	29	9	n=200

Решение. Введём условные варианты:

Для подсчёта можно использовать преобразованные корреляционные таблицы. Вначале составляют таблицу, в которой записывают условные варианты(C₁ = 40, C₂ = 35).

vj	ui						nv
	-3	-2	-1	0	1	2
-2 -1 0 1 2	5 – – – –	7 20 – – –	– 23 30 10 –	– – 47 11 9	– – 2 20 7	– – – 6 3	12 43 79 47 19
nu	5	27	63	67	29	9	n=200

После этого составляют таблицу, в которой подсчитывают произведения и.

vj	ui
	-3	-2	-1	0	1	2
-2	-15 5 -10	-14 7 -14	–	–	–	–	-29	58
-1	–	-40 20 -20	-23 23 -23	–	–	–	-63	63
0	–	-30 30 0	–	0 47 0	2 2 0	–	-28	0
1	–	–	-10 10 10	0 11 11	20 20 20	12 6 6	22	22
2	–	–	–	0 9 18	7 7 14	5 3 6	13	26
	-10	-34	-13	29	34	12	–
	30	68	13	0	34	24		–

Таким образом,

Находим также и:

Таким образом,

По формулам

определяем средние квадратичные отклонения:

Подставляем рассчитанные данные в формулу для :

Затем рассчитываем по формулам

получаем

Подставляем полученные значения в уравнение регрессии:

окончательно получаем

Задача 5. Из двухмерной нормальной генеральной совокупности извлечена выборка объемом n = 122. Найден выборочный коэффициент корреляции r_в = 0,4. Проверить нулевую гипотезу Н₀ о равенстве нулю генерального коэффициента корреляции при уровне значимости =0,05 и конкурирующей гипотезе Н₁.

Решение. Находим

По условию конкурирующая гипотеза Н₁: r₁0, поэтому критическая область – двусторонняя. По уровню значимости =0,05 и числу степеней свободы l = 122 – 2 = 120 находим из таблицы значений распределения Стьюдента для двусторонней критической области t_кр= (0,05 ,120) = 1,98.

Так как Т_набл > t_кр, т.е. 4,79 > 1,98, нулевую гипотезу отвергаем, т.е. выборочный коэффициент значимо отличается от нуля, следовательно. X и Y коррелируемы.

Дополнительные задачи.

Задача 1.В результате измерений отклонений от номиналов высот моделей (х_i) и отливок к ним (у_j) получены следующие результаты:

0,9	1,22	1,32	0,77	1,3	1,2	1,32	0,95	0,45	1,3	1,2
-0,3	0,1	0,7	-0,3	0,25	0,02	0,37	-0,7	0,55	0,35	0,32

Cоставить корреляционную таблицу и вычислить коэффициент корреляции.

Решение. Разобьем весь интервал, в котором заключены значения признаков, на пять частей. Возьмем для х_i наименьшее значение 0,40 и наибольшее – 1,40, тогда ширина одного интервала будет равна 0,20. Наименьшее y_j=-0,7, а наибольшее – 0,7. Ширина интервала 0,28. Откладываем интервалы изменений х_i по горизонтали, а у_j – по вертикали; данные заносим в табл.

0,5 0,7 0,9 1,1 1,3 Таблица

xi yj	0,4-0,6	0,6-0,8	0,8-1	1-1,2	1,2-1,4	ny
-0,7- -0,42 -0,42- -0,14 -0,14-0,14 0,14-0,42 0,42-0,7	- - - - 1	- 1 - - -	1 1 - - -	- - - 2 -	- 1 1 2 1	1 3 1 4 2
nx	1	1	2	2	5	n=11

- 0,56

- 0,28

0

0,28

0,56

Определим коэффициент корреляции. Для этого найдем средние значения и, предполагая, чтох_i и у_j - середины соответствующих интервалов:

,

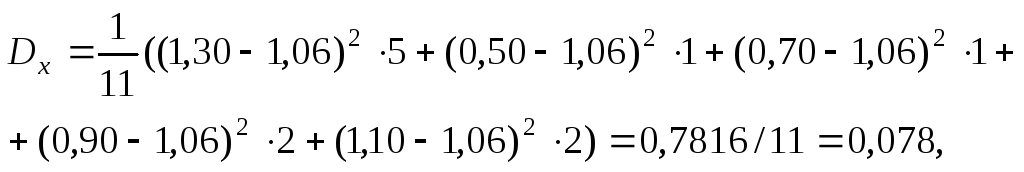
Коэффициент корреляции близок к единице, следовательно, между случайными величинами Х и Y достаточно тесная корреляционная связь.

Задача 2. Распределение 40 заводов области по количествуY ремонтных слесарей и числу X станко-смен представлено следующей корреляционной таблицей (табл.7)

Таблица 7

Y X	10 – 15	15 – 20	20 – 25	25 – 30	30 – 35	35 – 40	nx
0 – 0,2 0,2 – 0,4 0,4 – 0,6 0,6 – 0,8 0,8 – 1,0 1,0 – 1,2	4 2 - - - -	- 2 - 6 - -	- - 2 - - -	- - - 4 - -	- - - 4 6 -	- - - - 6 4	4 4 2 14 12 4
ny	6	8	2	4	10	10	n= 40

Составить уравнение прямой регрессии, установить тесноту связи между признаками. Для каждого интервала значений Y вычислить фактические значения частных средних y_x и теоретические значения, найденные из уравнений регрессии.

Решение. За значения признаков примем середины интервалов и составим корреляционную таблицу в условных вариантах, приняв в качестве условных нулей C₁ = 0,7 и C₂ = 27,5. (Эти варианты имеют частоту, равную 4, и находятся в середине корреляционной таблицы.)

Таблица

 u	-3	-2	-1	0	1	2	nu
-3 -2 -1 0 1 2	4 2 - - - -	- 2 - 6 - -	- - 2 - - -	- - - 4 - -	- - - 4 6 -	- - - - 6 4	4 4 2 14 12 4
n	6	8	2	4	10	10	n= 40

Находим:

Найдем искомый коэффициент корреляции:

Вычислим :

Подставим полученные значения в уравнение регрессии:

или

Вычислим для каждого интервала изменения х фактические значения частных средних:

,

,

,

,

.

Вычислим для каждого интервала изменения х теоретические значения из полученного уравнения:

,

,

,

,

,

.

Cравнивая полученные значения, видим, что они близки к фактическим.

Задача 3. Найти уравнение параболической регрессии Y и Х для экспериментальных данных, помещенных в табл.

Таблица

хi уj	1	2	3	4	5	6	ny
1 2 3 4 5 6	2 1 - - - -	1 2 3 1 - -	- - 1 3 2 -	- - - 1 2 1	- - - - 2 1	- - - - 1 1	3 3 4 5 7 3
nx	3	7	6	4	3	2	n=25
	1,33	2,57	4,17	5,0	5,33	5,50

Решение. Ищем уравнение регрессии в виде

.

Для определения неизвестных коэффициентов а, b по МНК записываем систему нормальных уравнений:

(1)

и составляем вспомогательную таблицу (10).

Таблица 10

n x	x	nxx	nxx2	nxx3
3 7 6 4 3 2	1 2 3 4 5 6	3 14 18 16 15 12	3 28 54 64 75 72	3 56 162 256 375 432
nx=25	21	78	296	1284

Таблица 10

nxx4	yx	nxyx	nxxyx	nxx2yx
3 112 486 1024 1875 2592	1,33 2,57 4,17 5,0 5,33 5,50	3,99 17,99 25,02 20,00 15,99 11,00	3,99 35,98 75,06 80,00 79,95 66,00	3,99 71,96 225,18 320,00 399,75 396,00
6092	23,9	93,99	340,98	1416,88

Теперь уравнения (1) примут вид:

Для упрощения расчетов разделим каждое уравнение на коэффициент при с:

Решив полученную систему, найдем: a= - 0,19, b= 2,21, c = 0,89.

Уравнение регрессии имеет вид

y_x = -0,19х² + 2,21х – 0,89.

Подставив в это уравнение в место х его значения, получим теоретические значения средних :

х	1	2	3	4	5	6
	1,14	2,78	4,07	4,91	5,41	5,52

Сравнивая теоретические значения частных средних с экспериментальными, видим, что они достаточно близки.

Задача 4. Зависимость между суточной выработкой продукции Y (т) и величиной основных производственных фондов X (млн руб.) для совокупности 50 однотипных предприятий представлена в таблице.

Вели- чина ОПФ, млн. руб.(X)	Середи- ны интер - валов	Суточная выработка продукции, т (Y)	Всего ni	Группо- вая сре - няя, т
		7-11 11-15 15-19 19-23 23-27
	yj xi	9 13 17 21 25
20-25 25-30 30-35 35-40 40-45	22,5 27,5 32,5 37,5 42,5	2 1 – – – 3 6 4 – – – 3 11 7 – – 1 2 6 2 – – – 1 1	3 13 21 11 2	10,3 13,3 17,8 20,3 23,0
Всего ni		5 11 17 14 3	50	–
Групповая средняя млн руб. 25,5 29,3 31,9 35,4 39,2 – –

Проверить значимость коэффициента корреляции между переменными X и Y.

Решение. Статистика критерия:

Для уровня значимости и числа степеней свободынаходим критическое значение статистики(см. табл. приложений). Посколькукоэффициент корреляции между суточной выработкой продукцииY и величиной основных производственных фондов Xзначимо отличается от нуля.

Домашнее задание.

Задача 1. Распредление 60 предприятий химической промышленности по энерговооружённости труда Y (кВт ∙ ч) и фондовооружённости X (млн руб.) дано в таблице

x y	0 – 4,5	4,5 – 9	9 – 13,5	13,5 – 18	18 – 22,5	Итого
0 – 1,4 1,4 – 2,8 2,8 – 4,2 4,2 – 5,6 5,6 – 7,0 7,0 – 8,4	4 4 2 – – –	1 2 8 1 – –	– – 1 20 3 –	– – – 4 3 1	– – – – 3 3	5 6 11 25 9 4
Итого	10	12	24	8	6	60

Необходимо: а) Построить эмпирические линии регрессии; б) оценить тесноту и направление связи между переменными с помощью коэффициента корреляции; проверить значимость коэффициента корреляции на уровне и построить для него 95%-ный доверительный интервал; в) вычислить эмпирические корреляционные отношения и оценить их значимость на 5%-ном уровне; г) на уровне значимости 0,05 проверить гипотезу о линейной корреляционной зависимости между переменнымиY и X; д) найти уравнения прямых регрессии, построить их графики и найти 95%-ные доверительные интервалы для коэффициентов регрессии.

Задача 2. Имеются следующие данные об уровне механизации работ X (%) и производительности труда Y (т/ч) для 14 однотипных предприятий:

xi	32	30	36	40	41	47	56	54	60	55	61	67	69	76
yj	20	24	28	30	31	33	34	37	38	40	41	43	45	48

Необходимо: а) оценить тесноту и направление связи между переменными с помощью коэффициента корреляции; проверить значимость коэффициента корреляции на уровне ; б) найти уравнения прямых регрессии.

Задача 3. При исследовании корреляционной зависимости между объёмом продукции X (единиц) и её себестоимости Y (тыс. руб.) получено следующее уравнение регрессии Y по X: Составить уравнение регрессииX по Y, если коэффициент корреляции между этими признаками оказалась равным -0,8, а средний объём продукции единиц.

Задача 4. При исследовании корреляционной зависимости между ценой на нефть X и индексом нефтяных компаний Y получены следующие данные: (ден.ед.),(усл. ед.), Необходимо: а) составить уравнения регрессии Y по X и X по Y; б) используя соответствующее уравнение регрессии, найти среднюю величину индекса при цене на нефть 16,5 ден. ед.

Ответы:

1). б) r = 0,872; связь тесная и прямая, r значим, так как t= =13,57 > (с помощьюz - преобразования Фишера); в) (значим, так какF = =50,4 > (значим, так какF = =47,6 > г) гипотеза о линейной корреляционной зависимости не отвергается, ибоблизко ктак, чтоF=2,10 < (илиблизко ктак, чтоF = =2,47 > ); д)

2). а) r = 0,969; связь очень тесная и прямая; r значим (так как t = б)

3).

4). а)б)(усл. ед.).

184