Системы случайных величин

Смоленск 2006

Двумерной называют случайную величину (X, Y), каждое возможное появление которой представляет собой пару чисел (x, y).

Случайные величины X и Y, рассматриваемые совместно, образуют систему двух случайных величин.

Общей характеристикой двумерной случайной величины является функция распределения вероятностей, которая представляет собой вероятность события (X < x, Y < y):

Для дискретной случайной величины распределение может быть задано в виде таблицы распределения, в которой каждой паре значенийставится в соответствие вероятность появления этой пары

Функция распределения вероятностей непрерывной случайной величины выражается через двумерную плотность вероятности по формуле

Вероятность совместного появления пары дискретных случайных величин можно записать в виде

где случайные вероятности.

Для непрерывных случайных величин плотность вероятности записывается в виде

Среди числовых характеристик двумерной случайной величины важнейшими являются условное математическое ожидание и ковариация.

Условным математическим ожиданием дискретной случайной величины Y при X = x называют сумму произведений возможных значений Y на их условные вероятности

Для непрерывных случайных величин условное математическое ожидание определяется интегралом:

Условное математическое ожидание M(Y / X = x) называется также регрессией величины Y на X.

Аналогично определяется регрессия X на Y:

для дискретной случайной величины

для непрерывной случайной величины

Ковариацией или корреляционным моментом случайных величин X и Y называется математическое ожидание произведения отклонений этих величин от их математических ожиданий:

Коэффициентом корреляции r_xy случайных величин X и Y называется отношение ковариации к произведению средних квадратичных отклонений этих величин:

Линейной средней квадратической регрессией Y на X называется функция вида

где

Цель занятия: 1. Добиться усвоения различных форм задания закона распределения для системы случайных величин.

2. Выработать навыки вычисления числовых характеристик системы случайных величин и вероятности попадания в данную область.

3. Уяснить необходимые и достаточные условия независимости случайных величин.

Студенты к этому практическому занятию должны подготовить ответы на следующие вопросы.

1. Как можно трактовать систему случайных величин?

2. Что называется условным законом распределения?

3. Как выражается плотность распределения каждой из величин, входящих в систему, через плотность системы?

4. В чем различие и связь между вероятностной и функциональной зависимостями?

5. Следует ли для системы двух случайных величин: независимость из некоррелированности? Зависимость из некоррелированности? Некоррелированность из независимости? Коррелированность из зависимости?

Задача 1. Найти распределения составляющих двухмерной случайной величины (для деталей, работающих на изгиб X и кручение Y), заданной следующей таблицей:

X Y	x1	x2	X3
y1	0,18	0,22	0,16
y2	0,08	0,16	0,20

Решение. Сложив вероятности по столбцам, получим вероятности возможных значений для деталей, работающих на изгиб X:

Ряд распределения составляющей X имеет вид:

X	x1	x2	x3
P	0,26	0,38	0,36

Контроль: 0,26 + 0,38 +0,36 = 1.

Сложив вероятности по строкам, получим вероятности возможных значений нагрузок для деталей, работающих на кручение Y:

Ряд распределения составляющей Y имеет вид:

Y	Y1	y2
P	0,56	0,44

Контроль: 0,56 + 0,44 = 1.

Задача 2. Функция распределения системы двух случайных величин (X, Y) имеет вид

Найти плотность распределения вероятностей f(x, y).

Решение.

Отсюда

Задача 3. Плотность распределения вероятностей случайного вектора X(X,Y) имеет вид

Определить константу С и плотность распределения вероятностей компоненты Y.

Решение. Так как случайные величины X, Y изменяются в замкнутой области, то

Следовательно,

т. е. С=2;

Задача 4. Найти регрессию величины Y на X для двух значений ина основе заданной таблицы распределения двумерной случайной величины

X Y	3	6
10	0,25	0,10
14	0,15	0,05
18	0,32	0,13

Решение. Условное математическое ожидание, или регрессия, величины Y на X находится на основе соотношения

где

Определяем P(X = 3) и P(X = 6):

Вычисляем условные вероятности:

Находим условные математические ожидания:

Задача 5. Задан закон распределения двумерной случайной величины (X, Y)

Y X	2	3	5
1	0,10	0,20	0,15
3	0,05	0,14	0,11
4	0,12	0,08	0,05

Найти коэффициент корреляции между величинами X и Y.

Решение. Находим вероятности значений X = 1, X = 3, X = 4:

Определяем вероятности значений Y = 2, Y = 3, Y = 5:

Находим M(Y):

Определяем M(X):

Вычисляем M(X²) и M(Y²):

Находим

Откуда

Ковариация величин X и Y может быть найдена по формуле

Итак,

Задача 6. Изготавливаемые в цехе втулки сортируются по отклонениям внутреннего диаметра от номинального на четыре группы по значениям 0,01, 0,02, 0,03, 0,04 мм и по овальности – на четыре группы по значениям 0,02, 0,04, 0,06, 0,08. Распределения отклонений диаметра X и овальности Y приведены в табл. 2 и 3 соответственно.

Таблица 2

xi yi	0,01	0,02	0,03	0,04
0,02	0,01	0,02	0,04	0,04
0,04	0,03	0,24	0,15	0,06
0,06	0,04	0,10	0,08	0,08
0,08	0,02	0,04	0,03	0,02

Таблица 3

xi	0,01	0,02	0,03	0,04
pi	0,10	0,40	0,30	0,20
yj	0,02	0,04	0,06	0,08
pj	0,11	0,48	0,30	0,11

Найти условные вероятности P (X = x_i/ y = 0,06 ) и условную функцию распределения отклонения внутреннего диаметра от номинального втулок, отнесенных в группу по овальности 0,06: F (x / y = 0,06).

Решение. Условные вероятности:

P (x = 0,01 / y = 0,06) = =,

P (x = 0,02 / y = 0,06) = =,

P (x = 0,03 / y = 0,06) = =,

P (x = 0,04 / y = 0,06) = =.

Контроль: 0,13 + 0,33 + 0,27+ 0,27 = 1.

Найдем условную функцию распределения (F (х / y = 0,06)). По определению

F (x / y = 0,06) =

Задача 7. Поверхность распределения системы случайных величин (X, Y) представляет собой прямой круговой конус, основанием которого служит круг с центром в начале координат и радиусом r₀. Вне этого круга плотность распределения вероятностей равна нулю. Найти плотность распределения вероятностей f(x, y) системы, плотности распределения вероятностей величин, входящих в систему: f₁( x ), f₂ ( y ), условные плотности распределения вероятностей f₁ (x / y ) и f₂ (x / y ) и определить, являются ли случайные величины зависимыми.

Решение. Имеем

Плотности распределения вероятностей отдельных случайных величин X, Y, входящих в систему (X, Y), выразятся через плотность распределения вероятностей системы:

, ,

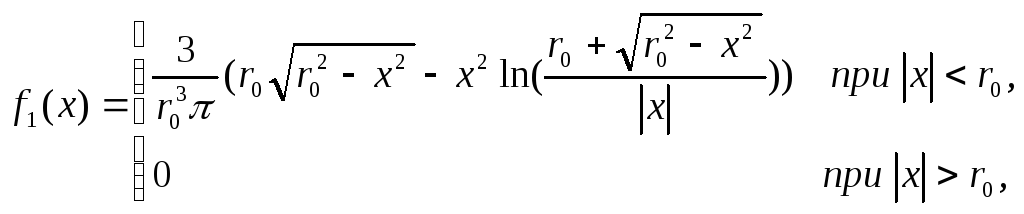
Условные плотности распределения f (x / y) и f (y / x) выражаются через безусловные, т.е.

Так как , то случайных величин X и Y зависимы.

Задача 8. Плотность распределения вероятностей случайных величин X и Y (координат амплитуд колебаний кузова автомобиля при движении)

f(x, y) =

Найти: 1) математические ожидания составляющих системы; 2) дисперсии D(X), D(Y); 3) корреляционный момент .

Решение.1.

M(X)=0,5,

M(Y) = 0,5.

2. Найдем дисперсию:

Так как выражение для D(Y) имеет такой же вид, как и для D(X),то можем записать, что D(Y) = .

3.

Задача 9. Производится штамповка детали, имеющей форму эллипса

.

Отклонение оси пуансона в результате износов распределено по нормальному закону с параметрами =1,=1,=1,=2,=0. Найти вероятность того, что деталь из-под штампа выйдет годной.

Решение. Область D штампованной детали ограничена эллипсом рассеивания с полуосями а == 1,b = =2, а вероятность попадания в эту область

Р ((x, у)Е) = 1 – е0,393