Нахождение пределов с использованием свойств эквивалентных бесконечно малых функций

Задача №4. Применить свойства эквивалентных величин к нахождению пределов:

1)

2)

3)

4)

5) так как (по теореме о сумме конеч-

ного числа бесконечно малых) .

6) .

7)

Задачи для самостоятельного решения:

1. Найти пределы:

1);

2) ;

3) ;

4) ;

5) ;

6) .

2. Сравнить порядок функций:

1) ;

2) ;

3) ;

4) ;

5) ;

6) .

Занятие 12. Непрерывность и точки разрыва функции.

Для усвоения практического материала нужно ответить на следующие теоретические вопросы:

1. Определение непрерывности функции в точке.

2. Действия над непрерывными функциями.

3. Односторонние пределы и односторонняя непрерывность.

4. Непрерывность основных элементарных функций.

5. Точки разрыва функций и их классификация.

6. Свойства функций непрерывных на отрезке.

Типовые задачи

Задача 1. Используя лишь определение, доказать непрерывность функции

.

Решение.

Задача 2. Используя лишь определение, доказать непрерывность функции

.

Решение.

Задача 3. Найти .

Решение.

Так как

(в силу непрерывности логарифмической функции).

Частный случай: .

Задача 4. Найти .

Решение.

Пусть , тогдаи при(так как показательная функция непрерывна).

Тогда

Частный случай: если , то.

Задача 5. Исследовать на непрерывность, найти точки разрыва, указать характер разрыва, в случае устранимого разрыва доопределить до непрерывной функцию

.

Решение.

непрерывна на .

(точка устранимого разрыва.

Если , то функциябудет непрерывной в точке.

Задача 6. Показать, что для функции точкаявляется точкой разрыва первого рода.

Решение.

По определению модуля числа , когдаили.

, когда или.

Так как , то точка– точка разрыва 1 рода. Конечный скачок функции.

Данную функцию нельзя доопределить так, чтобы она была непрерывной в точке .

Задача 7. Исследовать на непрерывность функцию

Решение.

()точка разрыва 2 рода.

В точке функция меняет аналитическое выражение.

()конечный разрыв 1 рода.

Скачок функции .

Задачи для самостоятельного решения:

1. Исследовать на непрерывность и изобразить графически функции:

1) ;

2) ;

3) ;

4) ;

5)

6)

2. Задана функция . При каком выборе параметров, входящих в определение,будет непрерывной?

1)

2)

Занятие 13. Нахождение производных функции одной переменной

Для усвоения практического материала нужно ответить на следующие теоретические вопросы:

1. Определение производной функции одной переменной.

2. Геометрический, экономический смысл производной.

3. Таблица основных производных.

4. Правила дифференцирования.

Типовые задачи

1. Нахождение производной функции по определению

Задача № 1.Для функциивычислитьи, соответствующие изменениям аргумента отдо.

Решение.

;

Задача № 2. Найти производные функций, пользуясь определением:

Решение.

Решение.

так как

2. Нахождение производных с помощью таблицы производных

Задача № 3. Найти производные функций:

Задача № 4. Найти угловой коэффициент секущей к параболе, если она проходит через точки с абсциссами.

Решение.

Задача № 5. Найти уравнение касательной и нормали к кривойв точке.

Решение.

Уравнение касательной к кривой в точке

.

Уравнение нормали к кривой в точке

.

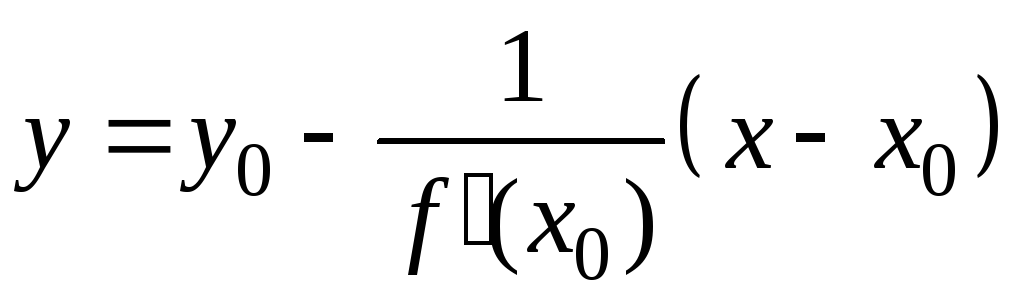или

– уравнение касательной,

– уравнение нормали.