
- •Типовые примеры Действия над матрицами
- •Типовые примеры Вычисление определителей
- •Обратная матрица
- •Типовые примеры Решение систем линейных уравнений методом Крамера
- •Решение систем линейных уравнений методом обратной матрицы
- •Типовые задачи
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Типовые задачи
- •1. Уравнение прямой на плоскости.
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •1. Множества и операции над ними.
- •2. Декартово произведение.
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Задания для самостоятельного решения:
- •Типовые задачи
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Нахождение пределов с использованием свойств эквивалентных бесконечно малых функций
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Нахождение производных с помощью таблицы производных
- •Задачи для самостоятельного решения:
- •1.Нахождение производных сложных функций, заданных явно
- •2. Дифференциал функции одной переменной
- •3. Производные и дифференциалы высших порядков
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Задачи для самостоятельного решения:
Решение систем линейных уравнений методом обратной матрицы
Задача №5. Найти решение системы методом обратной матрицы:

Решение.
Здесь
![]() ,
так что матрица А невырожденная и искомое
решение имеет вид
,
так что матрица А невырожденная и искомое
решение имеет вид![]() .
.
 .
.
Отсюда
![]()
Задача №6. Решить систему уравнений матричным методом:

Решение.
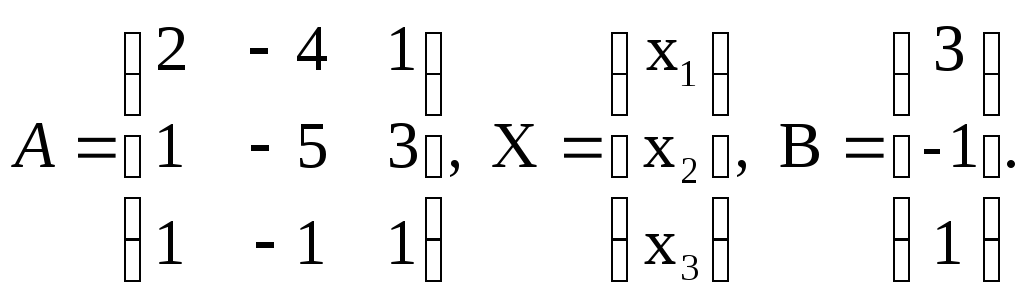
![]()

Находим:

т.е.
![]() – решение данной системы.
– решение данной системы.
Задачи для самостоятельного решения:
Решить системы уравнений методом Крамера и методом обратной матрицы.
1.
 2.
2.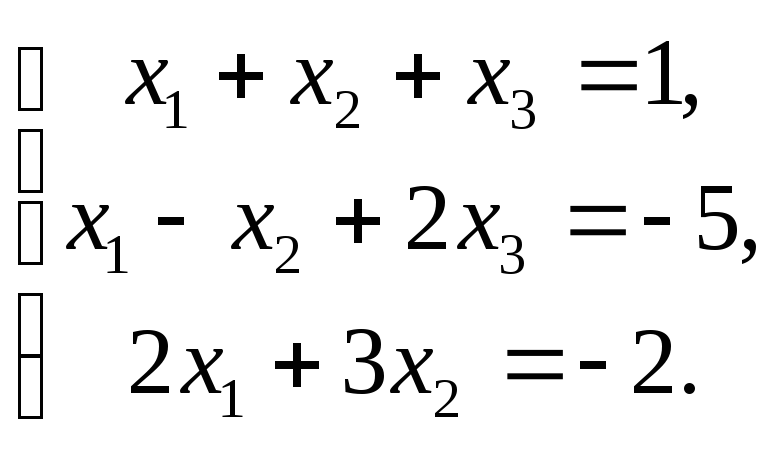
3.
 4.
4.
5.
 6.
6.
Занятие 4. Решение систем линейных уравнений методом Гаусса.
Для усвоения практического материала нужно ответить на следующие теоретические вопросы:
Понятие системы линейных алгебраических уравнений.
Понятие решения системы линейных алгебраических уравнений.
Определение совместной и несовместной системы.
Достаточное условие совместной системы.
Определение однородной и неоднородной системы.
Определение ранга матрицы.
Алгоритм решения неоднородной системы линейных уравнений методом Гаусса.
Алгоритм решения однородной системы линейных уравнений.
Типовые задачи
Задача №1. Решить систему методом Гаусса:

Решение.
В результате элементарных преобразований над расширенной матрицей системы

исходная система свелась к ступенчатой:

Поэтому
общее решение системы: ![]()
Если
положить, например, ![]() ,
то
найдем одно из частных решений этой
системы
,
то
найдем одно из частных решений этой
системы ![]() ;
;![]() .
.
Задача №2. Решить систему методом Гаусса:

Решение.
Произведем элементарные преобразования над строками расширенной матрицы системы:
 .
.
Полученная матрица соответствует системе

Осуществляя
обратный ход, находим ![]()
Задача №3. Решить систему методом Гаусса:
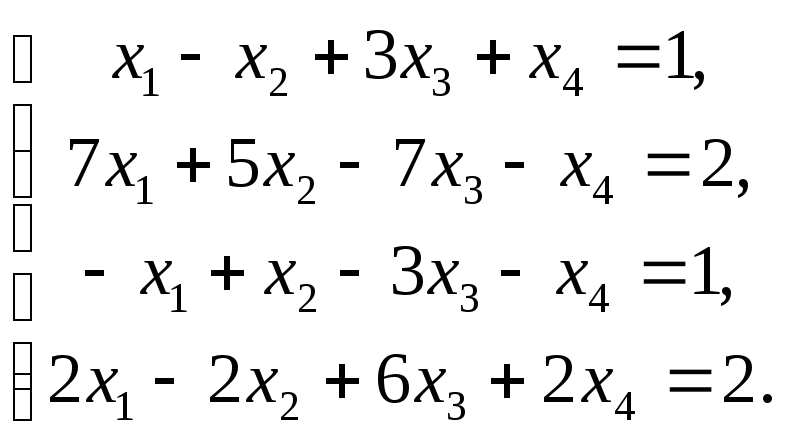
Решение:
 .
.
Наличие противоречивой строки говорит о несовместности системы линейных уравнений.
Задача №4. Решить однородную систему линейных уравнений методом Гаусса:

Решение.
Ранг
основной матрицы системы равен рангу
расширенной матрицы и равен числу
неизвестных. Система имеет единственное
решение, т.е. нулевое (тривиальное):
![]()
Задача №5. Решить однородную систему линейных уравнений методом Гаусса:

Решение.
 Ранг
основной матрицы системы равен рангу
расширенной матрицы и меньше числа
неизвестных (3<4). Система имеет
бесконечно много решений. Получим
систему:
Ранг
основной матрицы системы равен рангу
расширенной матрицы и меньше числа
неизвестных (3<4). Система имеет
бесконечно много решений. Получим
систему:
Е сли
положить
сли
положить![]() то
то![]() и
получиличастное
решение исходной системы.
и
получиличастное
решение исходной системы.
Задачи для самостоятельного решения:
I. Решить системы линейных уравнений:
1.
2.

3.

4.

5.

6.
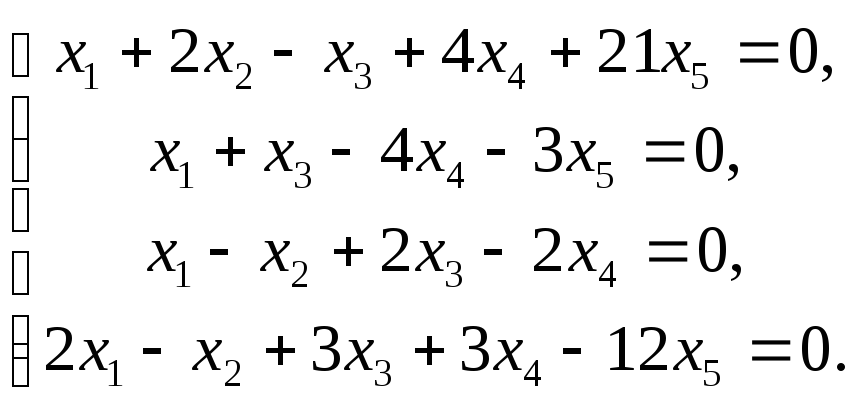
II. Найти решение системы
линейных уравнений в зависимости от
параметра![]() :
:
1.

2.

3.
Занятие 5. Скалярное, векторное и смешанное произведения векторов..
Для усвоения практического материала нужно ответить на следующие теоретические вопросы:
Дать определение скалярного произведения векторов.
Перечислить свойства скалярного произведения векторов.
Скалярное произведение векторов в координатной форме.
Приложения скалярного произведения для нахождении.
Какое произведение векторов называется векторным?
Перечислить свойства векторного произведения.
Какие приложения имеет векторное произведение в геометрии и механике?
Записать условие коллинеарности (параллельности) векторов.
Какое произведение векторов называется смешанным?
Перечислить свойства смешанного произведения. Его геометрический смысл.
Как выражается смешанное произведение через координаты?
