
- •Типовые примеры Действия над матрицами
- •Типовые примеры Вычисление определителей
- •Обратная матрица
- •Типовые примеры Решение систем линейных уравнений методом Крамера
- •Решение систем линейных уравнений методом обратной матрицы
- •Типовые задачи
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Типовые задачи
- •1. Уравнение прямой на плоскости.
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •1. Множества и операции над ними.
- •2. Декартово произведение.
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Задания для самостоятельного решения:
- •Типовые задачи
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Нахождение пределов с использованием свойств эквивалентных бесконечно малых функций
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Нахождение производных с помощью таблицы производных
- •Задачи для самостоятельного решения:
- •1.Нахождение производных сложных функций, заданных явно
- •2. Дифференциал функции одной переменной
- •3. Производные и дифференциалы высших порядков
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Задачи для самостоятельного решения:
- •Типовые задачи
- •Задачи для самостоятельного решения:
Обратная матрица
Задача №6. Найти матрицу, обратную
к матрице![]() .
.
Решение.
1) Найдем
![]()
![]() ,
следовательно обратная матрица
существует.
,
следовательно обратная матрица
существует.
2) Найдем алгебраические дополнения к элементам матрицы А
![]()
![]()
![]()
![]()
![]()
3) Запишем союзную матрицу
![]()
4) Найдем обратную матрицу
![]()
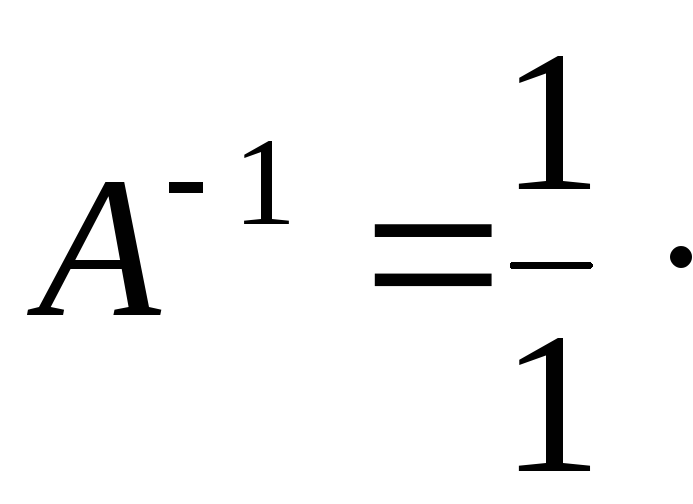
![]()
![]()
5) Сделаем проверку

![]()
![]()
Задача №7. Найти матрицу, обратную
к матрице .
.
Решение.
1) Найдем

![]() ,
следовательно обратная матрица
существует.
,
следовательно обратная матрица
существует.
2) Найдем алгебраические дополнения элементов матрицы А
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3) Запишем союзную матрицу

4) Найдем обратную матрицу
![]()



5) Сделаем проверку
![]()



Задача №8. Найти матрицу, обратную
к матрице .
.
Решение.
1) Найдем

![]() ,
следовательно обратная матрица
существует.
,
следовательно обратная матрица
существует.
2) Найдем алгебраические дополнения к элементам матрицы А
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3) Запишем союзную матрицу

4) Найдем обратную матрицу
![]()



5) Сделаем проверку
![]()



Задача №9. С помощью
элементарных преобразований строк
найти матрицу, обратную .
.
Решение.
Припишем к матрице
![]() справа единичную матрицу и будем
выполнять элементарные преобразования
строк объединенной матрицы до тех пор
справа единичную матрицу и будем
выполнять элементарные преобразования
строк объединенной матрицы до тех пор
Задача №10. Найти ранг матрицы
Решение.


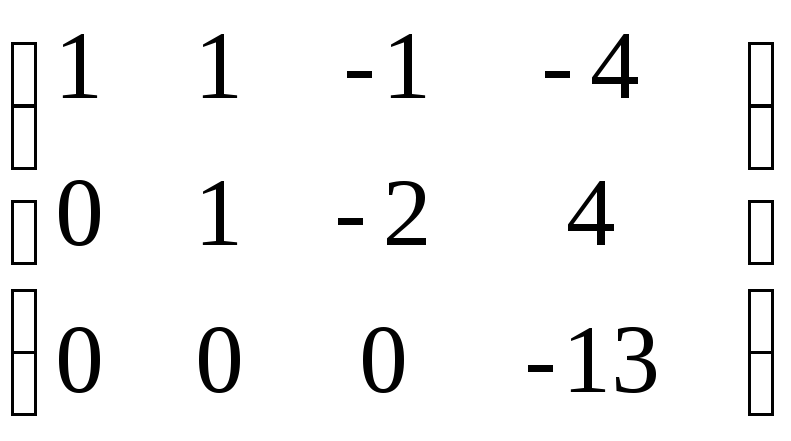
Ранг матрицы равен 3.
Задачи для самостоятельного решения:

а) по правилу треугольника;
б) с помощью разложения по первой строке;
в) преобразованием, используя свойства определителей.
2. Найти
минор и алгебраическое дополнение
элемента a13 определителя и вычислить его разложением по элементам
строки или столбца.
и вычислить его разложением по элементам
строки или столбца.
3. Решить уравнение

4. Вычислить определитель 4-го порядка
разложением по элементам строки или
столбца:

5. Найти обратную матрицу для следующих матриц:
 ;
2)
;
2) ;
3)
;
3) ;
4)
;
4) .
.
6. Решить матричные уравнения:
1)
![]() ;
;
2)
 ;
;
3)
![]() ;
;
4)
 ;
;
5)
 ;
;
6)
 ;
;
7)![]() ;
;
8) .
.
7. Доказать, что если А – квадратная матрица и (А+Е)2=О, то матрица А имеет обратную. Найти обратную для А матрицу.
8. Найти все матрицы второго порядка, для которых А-1=А.
Занятие 3. Решение систем линейных уравнений методом Крамера и методом обратной матрицы.
Для усвоения практического материала нужно ответить на следующие теоретические вопросы:
Понятие системы линейных алгебраических уравнений.
Понятие решения системы линейных алгебраических уравнений.
Определение совместной и несовместной системы.
Достаточное условие совместной системы.
Определение однородной и неоднородной системы.
Формулы Крамера.
Алгоритм решения систем линейных уравнений с помощью обратной матрицы.
Типовые примеры Решение систем линейных уравнений методом Крамера
Задача №1. Решить систему:

Решение.
Определитель системы:
![]()
![]() поэтому
ее решение определяется по формулам
Крамера:
поэтому
ее решение определяется по формулам
Крамера:
![]()
Но
 ,
,
Тогда
![]()
![]()
![]()
Задача №2. Решить систему:

Решение.
Определитель данной системы
![]() но
определитель
но
определитель![]() что говорит о несовместности системы.
Геометрически это означает, что данные
прямые не пересекаются, т.е. параллельны.
что говорит о несовместности системы.
Геометрически это означает, что данные
прямые не пересекаются, т.е. параллельны.
Задача №3. Решить систему:

Решение.
Определители
![]() ,
так как у них строки пропорциональны.
Здесь оба уравнения системы определяют
одну и ту же прямую и решением системы
являются координаты любой точки этой
прямой. Отсюда следует, что система
имеет бесчисленное множество решений.
,
так как у них строки пропорциональны.
Здесь оба уравнения системы определяют
одну и ту же прямую и решением системы
являются координаты любой точки этой
прямой. Отсюда следует, что система
имеет бесчисленное множество решений.
Задача №4. Решить систему

Решение.
Вычисляем определители:

Так как
![]()
![]() ,
то данная система имеет единственное
решение. Находим его по формулам Крамера:
,
то данная система имеет единственное
решение. Находим его по формулам Крамера:
![]()
