Задачи для самостоятельного решения:

1.Используя определение производной, найти производные функций:

1) ;

2) ;

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

1. Найти производные функций, используя таблицу производных и правила дифференцирования:

   1. ;

   2. ;

   3. ;

   4. ;

   5. ;

   6. ;

   7. ;

   8. ;

   9. ;

   10. 

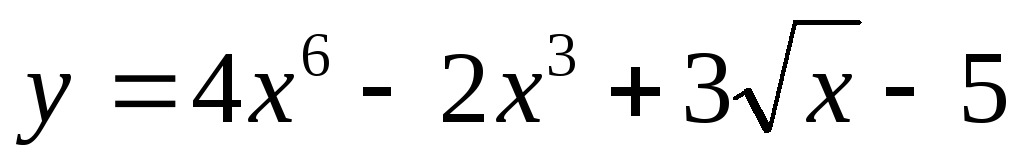2. Найти угловой коэффициент секущей к параболе 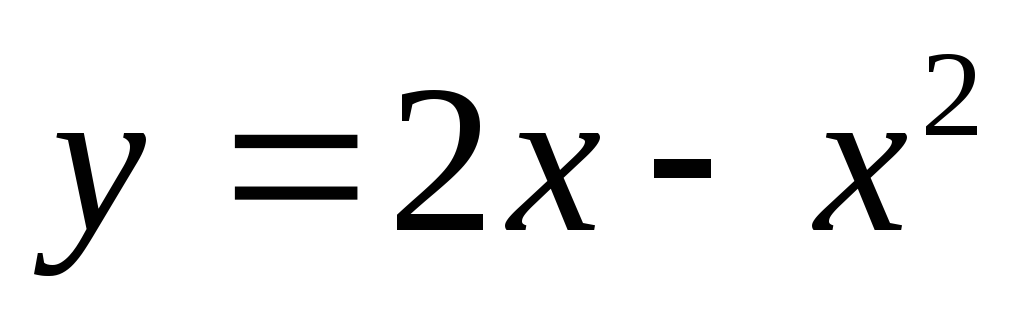, если она проходит через точки с абсциссами

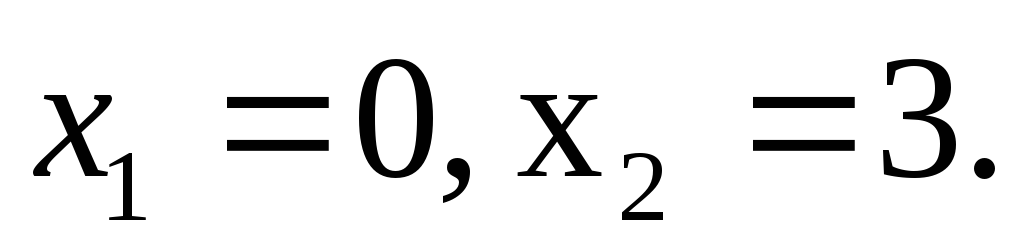
3. Найти уравнение касательной и нормали к кривой в точке.

Занятие 14. Производная сложной функции. Дифференциал и производная высших порядков

Для усвоения практического материала нужно ответить на следующие теоретические вопросы:

1. Определение производной функции одной переменной.

2. Определение производной сложной функции.

3. Задача (устно): найти производную y=2sin³5x.

4. Дифференциал функции. Связь дифференциала с производной. Теорема.

5. Инвариантность формы первого дифференциала. Применение дифференциала для приближённых вычислений.

6. Производные высших порядков.

1.Нахождение производных сложных функций, заданных явно

Задача №1.Найти производные функций:

1)

2) .

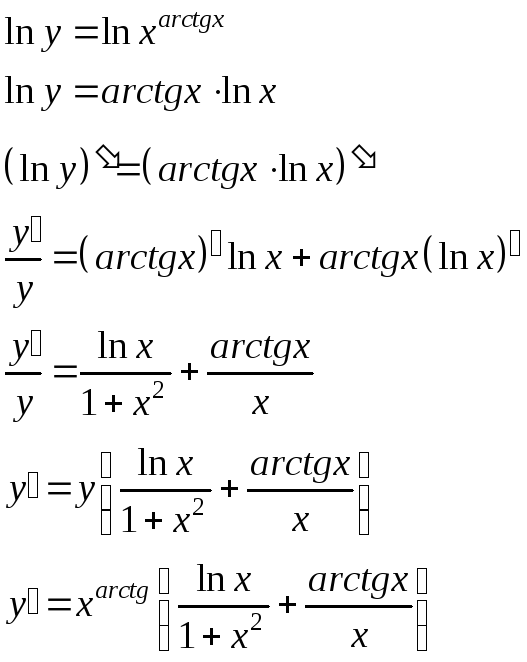
3)

4)

5)

6)

7) .

8) .

9)

2. Дифференциал функции одной переменной

Задача № 2. Найти приращениеи дифференциалdyфункцииприx=2,

Решение.

Задача № 3. Заменяя приращение функции дифференциалом, приближённо вычислитьarctg1,02.

Решение. Так как:

тогда

Задача № 4. Найтиdy функции:

1)

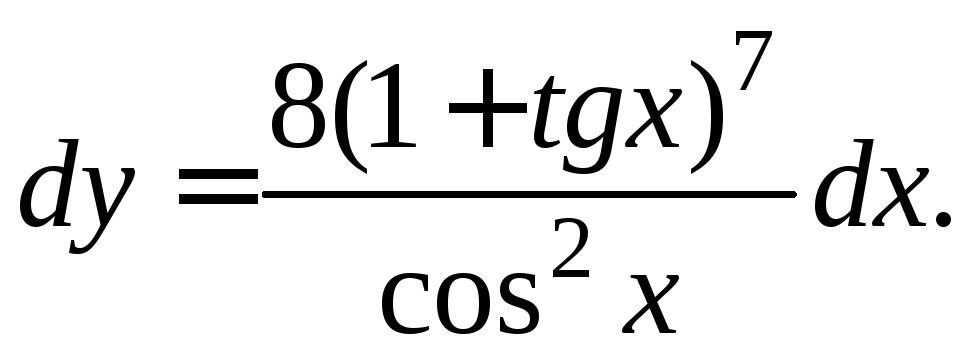
2)

3)

4)

5)

3. Производные и дифференциалы высших порядков

Задача № 5. Найти производнуюn-го порядка для функцииy = sinx.

Решение.

Задача № 6.Найтиесли

Решение

Задачи для самостоятельного решения:

1. Найти производные функций:

1) .

2) .

3) .

4) .

5)

6)

7) .

8) .

9)

10) .

11) .

12) .

13)

2. Найти производную функции в точке х_0:

3. Найти y^///: 1)

1)

2) y = x³lnх.

4. Заменяя приращение функции дифференциалом, найти приближённо

5. Заменяя приращение функции дифференциалом, найти приближённо ln1,01.

6. Найти d²y, если: 1)y = cos5x.

2) y= 3sin2x.

Занятие 15. Исследование функций и построение графиков

Для усвоения практического материала нужно ответить на следующие теоретические вопросы:

1. Определение возрастающей и убывающей функции.

2. Определение монотонной функции.

3. Определение локального максимума (минимума) функции.

4. Необходимые условия экстремума функции.

5. Достаточный признак экстремума функции.

Типовые задачи

Задача № 1. Исследовать функцию

Решение.

1. Область определения функции: .

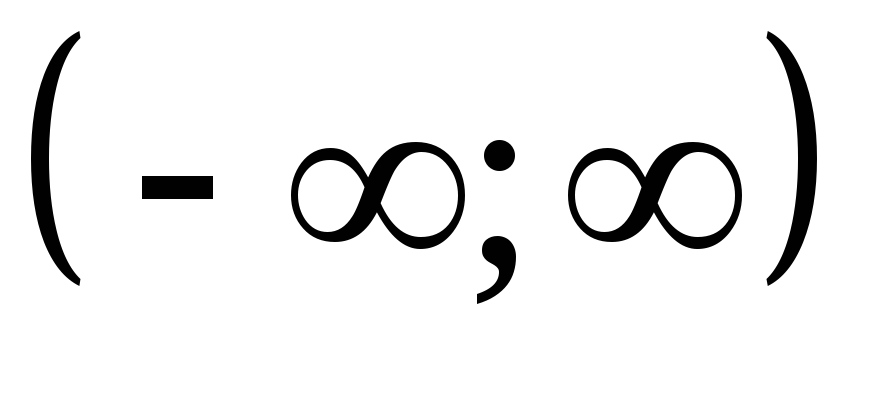2. Функция не имеет точек разрыва. Точки пересечения графика с осями координат:

;;

3. Выясним, является ли функция четной, нечетной или общего вида и периодичности.

Проверяем четность:

функция не является нечетной. Следовательно, функция общего вида.

Проверяем периодичность:

функция непериодическая.

4. Интервалы знакопостоянства функции.

Функция имеет производную всюду. ;– критические точки, т. к в них производная обращается в нуль.

а) ;функция возрастает

б) функция убывает

в) функция возрастает

Так как в точке х = 0 функция меняет знак с + на – , то в этой точке максимум, точка максимума.

Так как в точке х= 1 функция меняет знак с – на + , то в этой точке минимум,точка минимума.

5. Находим интервалы выпуклости, вогнутости и точки перегиба функции.

а) ;функция вогнутая

б) функция выпуклая

в) функция вогнутая

	–; –1/2		–1/2; 0	0		1/2		1	1; 
	+		–		–		+		+
	+		+		+		–		+
у		0		(0;1)		1/2		(1;0)
				Тmax				Tmin

Рис. 1

Задача № 2. Исследовать функцию.

Решение.

1. Область определения функции: .

2. Функция не имеет точек разрыва.

Точки пересечения с осями координат:

– нет точек пересечения с осью 0Х

3. Выясним, является ли функция четной, нечетной или общего вида и периодичности.

Проверяем четность :

– функция является четной.

Функция не является периодической

4. Интервалы монотонности функции.

Функция имеет производную всюду

х = 0 – критическая точка, так как в ней производная обращается в нуль.

а) ,

б) ,

так как в точке функция меняет знак с + на – , то в этой точке максимумточка максимума.

5. Найти интервалы выпуклости, вогнутости, точки перегиба.

а) ;функция вогнутая

б) функция выпуклая

в) функция вогнутая

– точки перегиба

	–;–1	–1	–1;0	0	0;1	1	1;
	+		–		–		–
	+		+		–		–
у		e-1/2 0,6		e0 = 1		e-1/2 0,6

Рис. 2

Задача № 3. Определить наибольшее и наименьшее значения функциина отрезке [–1; 4].

Решение. Определим точки максимума и минимума:

,

приx = 0 иx = 2. Точкиx₁ = 0 иx₂ = 2 являются критическими, для нихследовательно,

и

Вычислим значения функции на концах интервала:

Окончательно имеем:

Наибольшее значение при функция принимает в правом конце отрезка приx = 4. Наименьшее значение достигается в двух точках в точке минимума функции и на левом конце интервала, прих = –1.