Упражнения

1. Докажите, что если матрица Qневырождена, то ранги матрицA и Q^TAQ равны.

2. Найдите матрицы квадратичных форм ,,.

§4.2.2. Теорема Лагранжа

Теорема. Любую квадратичную форму с помощью невырожденного линейного преобразования неизвестных можно привести к виду, в котором коэффициент при квадрате первой переменной отличен от нуля.

Доказательство. Рассмотримквадратичную формугдеЕслиа₁₁0, то утверждение доказано. Еслиа₁₁= 0, но, скажема₂₂0, то изменим нумерацию неизвестных:

x₁ = y₂, x₂ = y₁, x₃ = y₃, … x_n = y_n.

Матрица этого линейного преобразования имеет вид:

,

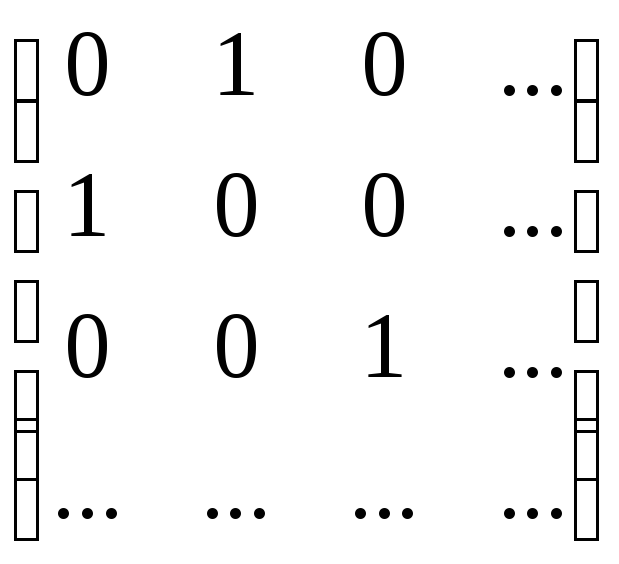невырожденная, так ее определитель равен -1. В преобразованной квадратичной форме коэффициент при уотличен от нуля.

Пусть теперь коэффициенты при квадратах всех переменных равны нулю, но а₁₂0. Тогда невырожденное линейное преобразование

приводит квадратичную форму к виду, в котором коэффициент при уотличен от нуля. Если же коэффициенты при квадратах всех переменных равны нулю иа₁₂= 0, но0, то изменив нумерацию переменных, сведем задачу к предыдущему случаю. ■

Квадратичная форма имеет канонический вид, если в ее записи нет слагаемых с произведениями неизвестных, т. е..

Теорема. (Лагранжа). Любую квадратичную форму с помощью невырожденного линейного преобразования неизвестных можно привести к каноническому виду.

Доказательство. С помощью невырожденного линейного преобразования приведем квадратичную формуf к виду, в котором а₁₁0. Все слагаемые, содержащиех₁, соберем в одну скобку и дополним эту скобку до полного квадрата, получим

,

где оставшиеся слагаемые образуют квадратичную форму g(x₂, …,x_n) от неизвестныхх₂, …,х_n. Невырожденное линейное преобразование неизвестных

приводит квадратичную форму к виду

.

Повторив рассуждения, с учетом того, что последовательное выполнение невырожденных линейных преобразований вновь невырожденное линейное преобразование, получим утверждение теоремы. ■

Пример. Приведите с помощью невырожденного линейного преобразования неизвестных к каноническому виду квадратичную форму f =.

Линейное преобразование приводит квадратичную форму к виду А линейное преобразование приводит к виду. Найдем сквозное линейное преобразование . Оно невырожденное, так как определитель матрицы линейного преобразования

равен – 2, то оно невырожденное.

Ответ: невырожденное линейное преобразование неизвестных приводит форму к каноническому виду

Квадратичная форма с действительными коэффициентами имеет нормальный вид, если в ее записи нет слагаемых с произведениями неизвестных, а квадраты переменных входят с коэффициентами 1 или -1 или совсем не входят. После изменения нумерации переменных нормальный вид можно переписать так: вначале идут коэффициенты 1, затем -1, а затем нули,

.

Теорема. Любую квадратичную форму с помощью невырожденного линейного преобразования неизвестных можно привести к нормальному виду.

Доказательство.Ограничимся доказательством возможности преобразования канонического видав нормальный вид с помощью невырожденного линейного преобразования:

, еслиa_i > 0 ;, еслиa_i < 0;, еслиa_i = 0. ■