
- •Модуль 4. Линейные операторы. Квадратичные формы Глава 4.1. Линейные операторы §4.1.1. Линейные операторы в линейном пространстве
- •Упражнения
- •§4.1.2. Ядро и образ линейного оператора
- •Упражнения
- •§4.1.3. Матрица линейного оператора
- •Упражнения
- •§4.1.4. Сумма и произведение линейных операторов
- •Упражнения
- •§4.1.5. Собственные векторы и собственные значения
- •Упражнения
- •§4.1.6. Самосопряженный линейный оператор
- •Упражнения
- •§4.1.7. Группа ортогональных матриц
- •Упражнения
- •§4.1.8. Ортогональный линейный оператор
- •Упражнения
- •Глава 4.2. Квадратичные формы
- •§4.2.1. Матричная запись квадратичной формы
- •Упражнения
- •§4.2.2. Теорема Лагранжа
- •Упражнения
- •§4.2.3. Закон инерции
- •Упражнения
- •§4.2.4. Положительно определенные квадратичные формы
- •Упражнения
- •§4.2.5. Приведение квадратичной формы к главным осям
- •§4.2.6. Билинейная форма
- •Упражнения
- •§4.2.7. Применение квадратичных форм к исследованию линий и поверхностей второго порядка
- •Упражнения
- •Глава 4.3. Каноническая форма Жордана
- •§4.3.1. Относительная линейная независимость
- •§4.3.2. Относительный базис
- •§4.3.3. Корневые векторы
- •Упражнения
- •§4.3.4. Корневое подпространство
- •Упражнения
- •§4.3.5. Канонический базис
- •§4.3.6. Циклическое подпространство
- •§4.3.7. Построение канонического базиса в корневом подпространстве
- •§4.3.8. Построение канонического базиса в общем случае
- •§4.3.9. Единственность канонической формы Жордана
§4.1.4. Сумма и произведение линейных операторов
Суммой двух линейных
операторов
![]() и
и![]() называется оператор
называется оператор![]() ,
для которого
,
для которого![]() .
.
Теорема. Если
![]() и
и![]() –
линейные операторы, действующие в
линейном пространствеV,
то
–
линейные операторы, действующие в
линейном пространствеV,
то
![]() +
+![]() – также линейный оператор, действующий
вV. ЕслиАиВ– матрицы линейных операторов
– также линейный оператор, действующий
вV. ЕслиАиВ– матрицы линейных операторов
![]() и
и![]() в базисее, то матрица суммы этих
линейных операторов в базисееравнаА + В.
в базисее, то матрица суммы этих
линейных операторов в базисееравнаА + В.
Доказательство. Непосредственно проверяется. ■
Произведением
![]() линейного оператора
линейного оператора![]() на элемент
на элемент![]() из поляKназывается
операторh =
из поляKназывается
операторh =
![]() ,
для которого
,
для которого![]() .
.
Теорема. Если![]() линейный оператор, действующий в линейном
пространствеV / K,
то
линейный оператор, действующий в линейном
пространствеV / K,
то![]() Kоператор
Kоператор![]() – также линейный. Матрица линейного
оператора
– также линейный. Матрица линейного
оператора![]() в базисееравна матрице линейного
оператора
в базисееравна матрице линейного
оператора![]() в этом базисе, умноженной на
в этом базисе, умноженной на![]() .
.
Доказательство. Непосредственно проверяется. ■
Теорема. МножествоU всех линейных операторов, действующих в линейном пространствеV размерностиnнад полем K, относительно введенных действий сложения и умножения на элемент поля K образует линейное пространство над полем K размерностиn2.
Доказательство проводится непосредственной проверкой всех аксиом линейного пространства. ■
Произведением
линейных операторов
![]() и
и![]() ,
действующих в линейном пространствеV/K,
называется операторg=
,
действующих в линейном пространствеV/K,
называется операторg=![]() ,
для которого
,
для которого![]() .
Определим также
.
Определим также![]() .
.
Теорема. Если
![]() и
и![]() линейные операторы, действующие в
линейном пространствеV/K,
то
линейные операторы, действующие в
линейном пространствеV/K,
то![]() – также линейный оператор. Матрица
линейного оператора
– также линейный оператор. Матрица
линейного оператора![]() в базисееравна произведению матрицыАлинейного оператора
в базисееравна произведению матрицыАлинейного оператора![]() на матрицуВлинейного оператора
на матрицуВлинейного оператора![]() .
.
Доказательство.(![]() )(е)
=
)(е)
=![]() (Ае)
=А
(Ае)
=А![]() е
= АВе
е
= АВе![]() (
(![]() )(е)
= АВе.■
)(е)
= АВе.■
Для ненулевого
многочлена f(t)
=
![]() значение многочлена от линейного
оператора f(А) =
значение многочлена от линейного
оператора f(А) =
![]() ,где
,где![]() – тождественное отображение.
– тождественное отображение.
Теорема. Гамильтона-Кэли. Линейный оператор является корнем своего характеристического многочлена.
Теорема была доказана для матриц. Здесь мы переформулировали ее для линейных операторов. ■
Упражнения
Найдите матрицы линейных операторов
 +
+ и
и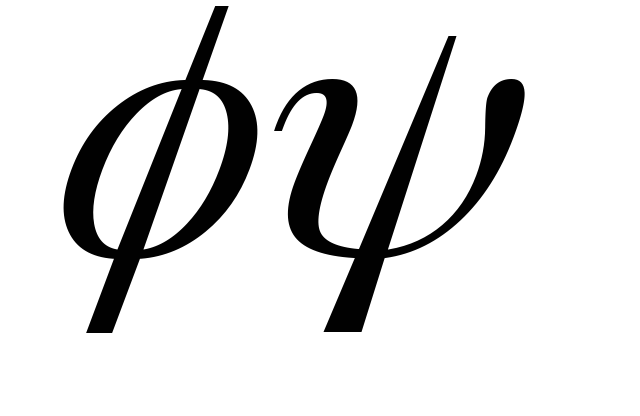 в базисе b1,b2, если матрица
в базисе b1,b2, если матрица в базисеа1=(-3; 7),а2= (1; -2) имеет вид
в базисеа1=(-3; 7),а2= (1; -2) имеет вид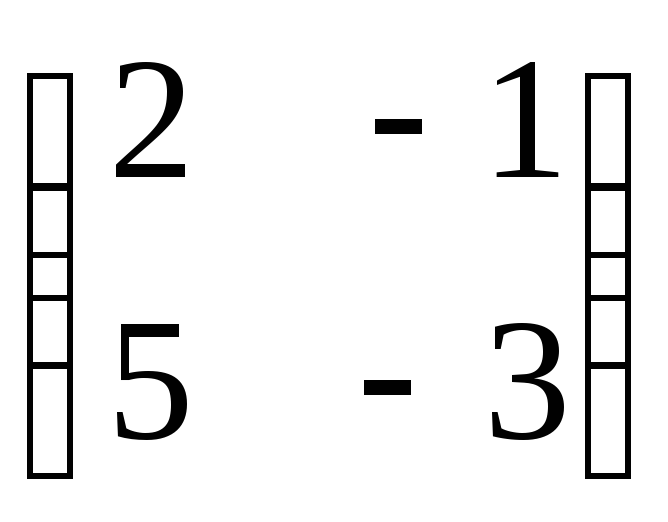 ,
а матрица
,
а матрица в базисеb1= (6;
-7),b2= (-5; 6) имеет
матрицу
в базисеb1= (6;
-7),b2= (-5; 6) имеет
матрицу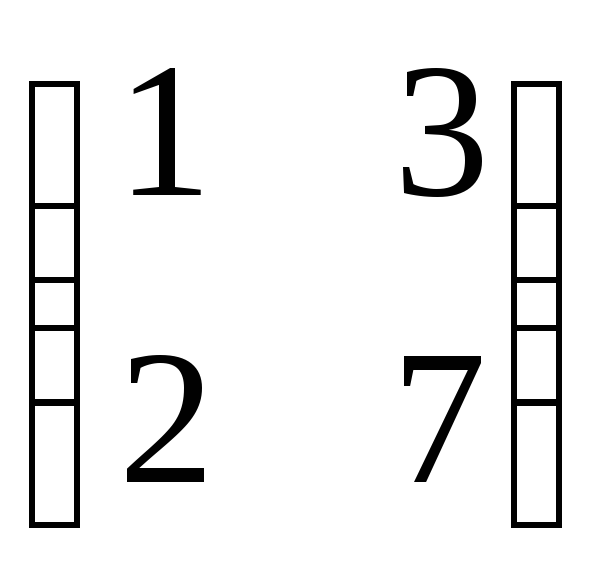 .
.Докажите, что линейное пространство всех линейных операторов, действующих в одномерном линейном пространстве, одномерно.
Линейное пространство
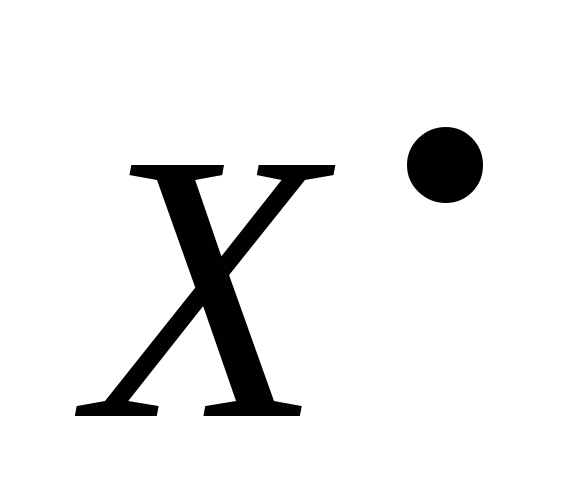 всех функционалов, действующих в
линейном пространствеХ/K,т.е. линейно отображающихX
в K, называетсясопряженным с пространствомХ.
Докажите, что сопряженное линейное
пространство
всех функционалов, действующих в
линейном пространствеХ/K,т.е. линейно отображающихX
в K, называетсясопряженным с пространствомХ.
Докажите, что сопряженное линейное
пространство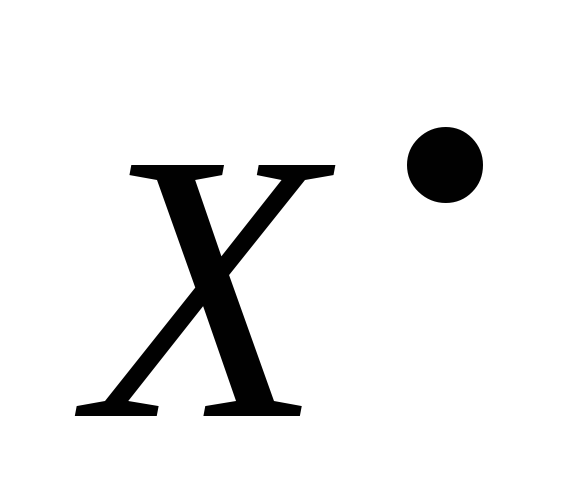 изоморфно линейному пространствуХ.
изоморфно линейному пространствуХ.Говорят, что ненулевой многочлен f(t) =
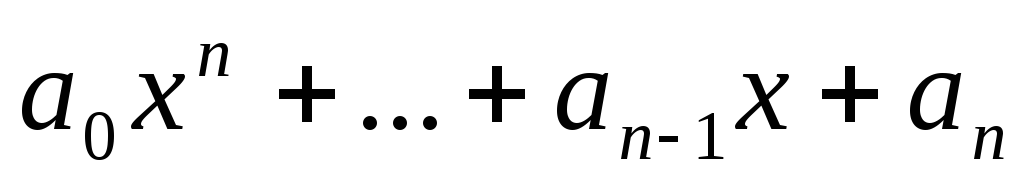 аннулирует оператор А,еслиf(А)
=
аннулирует оператор А,еслиf(А)
=
 .
Докажите, что для любого линейного
оператора, действующего вn-мерном
линейном пространстве, существует
аннулирующий многочлен степени
.
Докажите, что для любого линейного
оператора, действующего вn-мерном
линейном пространстве, существует
аннулирующий многочлен степени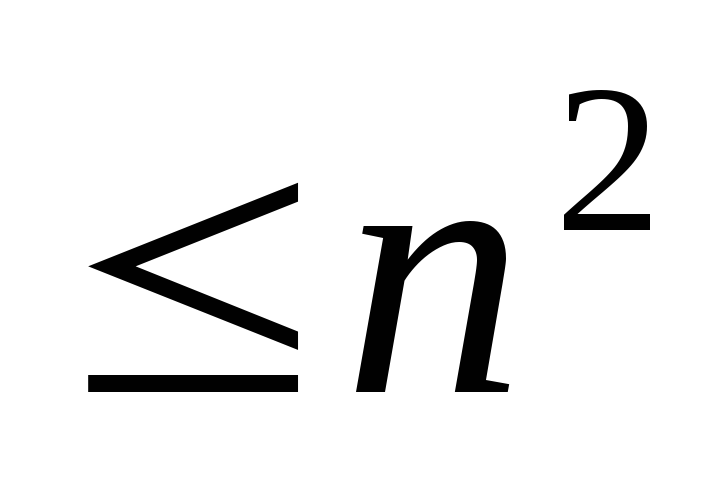 .
.Пусть m(t) – многочлен наименьшей степени среди всех многочленов, аннулирующих линейный оператор A. Докажите, что m(t) делит любой другой многочлен, аннулирующий линейный оператор A.
Докажите, что многочлен m(t) определен линейным операторомАединственным образом с точностью до умножения на постоянный ненулевой множитель. Многочленm(t) со старшим коэффициентом 1 называетсяминимальным многочленомлинейного оператораА.
Линейный оператор Аназываетсянильпотентным, если существует натуральное число q, для которого Aq =
 .
Наименьшее число q, для которого
Aq =
.
Наименьшее число q, для которого
Aq = ,
называетсяиндексом нильпотентности
линейного оператора А. Докажите, что
индекс любого нильпотентного линейного
оператора, действующего вn-мерном
линейном пространстве, не превосходитn.
,
называетсяиндексом нильпотентности
линейного оператора А. Докажите, что
индекс любого нильпотентного линейного
оператора, действующего вn-мерном
линейном пространстве, не превосходитn.Найдите минимальный многочлен для оператора проектирования, для оператора отражения, для нильпотентного оператора индекса q.
Докажите, что любые два многочлена от одного линейного оператора перестановочны.
Докажите, что если линейные операторы А иВ перестановочны, то и любые многочленыf(A) и g(A)от этих операторов перестановочны.
Докажите, что произведение линейных операторов А иВ тогда и только тогда невырождено, когда каждый из операторовА иВ невырожден. При этом
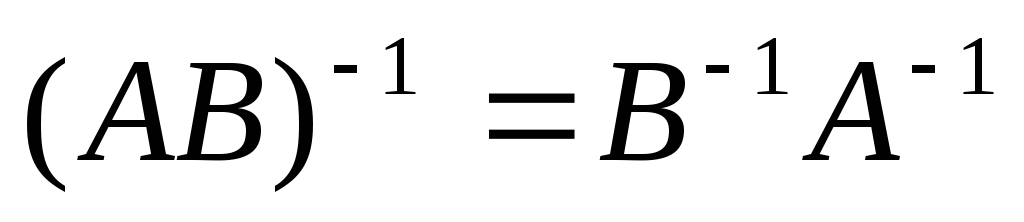 .
.Докажите, что для невырожденного линейного оператора А и любой константы
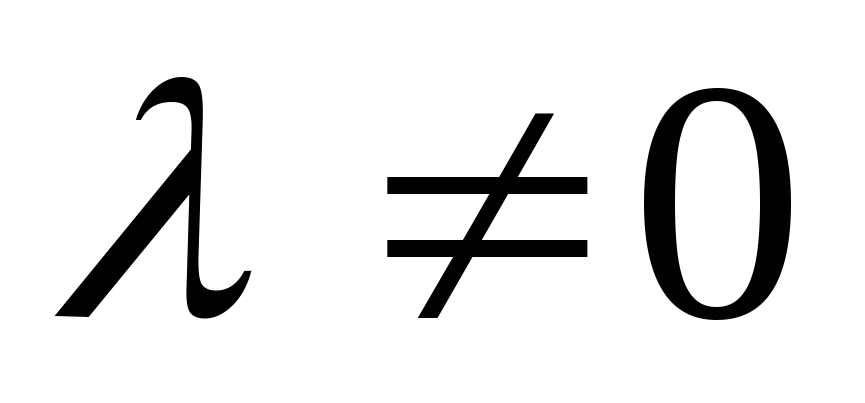
![]() .
.
Докажите, что невырожденные линейные операторы, действующие в линейном пространстве Х/K, являются автоморфизмами, т.е. изоморфизмамиХ на себя.
Докажите, что невырожденные линейные операторы, действующие в линейном пространстве Х/K, образуют мультипликативную группу.
