Упражнения и задачи

1. Если bисвзаимно просты,аделится наbиаделится нас, тоаделится наbc. Доказать.

2. Доказать, что аиbвзаимно просты тогда и только тогда, когда существуют целые числаииv, для которых

3. Доказать, что множество всех общих делителей чисел аиbсовпадает с множеством всех делителей их НОД.

4. Для пар чисел аиbнайти числаииv, для которых

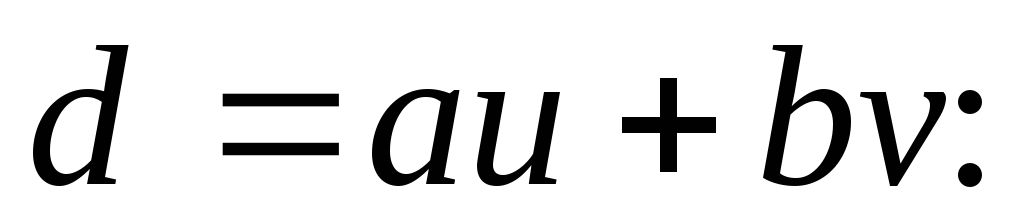
а) б)в)

г) д)

§1.1.4 Наименьшее общее кратное

Если число аделится на несколько чисел, то оно называется ихобщим кратным.Наименьшее положительное общее кратное называетсянаименьшим общим кратным. Для него применяют обозначения НОК

Теорема.Наименьшее общее кратное двух целых чиселаиbравно произведению этих чисел, деленному на их наибольший общий делитель, т.е.

НОК

Доказательство:Пустьт.е.Пусть такжеТогдаПо условиюделится наОтсюдаделится на. По теореме Евклидаделится на, т.е.Мы получили, что произвольное общее кратное можно записать в виде

Наименьшее положительное целое число такого вида при имеет видА это и требовалось доказать. ■

Следствие.Произвольное общее кратное чиселаиb есть кратное их наименьшего общего кратного.

Упражнения и задачи

1. Найти наименьшее общее кратное следующих систем чисел:

а) 544 и 128; б) 360 и 504; в) 24, 20 и 72; г) 28, 24 и 63.

2. Дано: НОД8, НОК96. Найтиаиb.

3. Сумма двух чисел 667, а отношение их НОК к НОД равно 120. Найти эти числа.

4. Доказать, что

§1.1.5 Простые числа

Число называется простым, если оно делится только на себя и 1. Например, числа 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ... простые. Числа, которые имеют кроме себя и 1 другие положительные делители называютсясоставными. Число 1 считается ни простым, ни составным. Оно действительно занимает в ряде натуральных чисел особое положение. Ведь оно имеет только 1 делитель, а все другие натуральные числа имеют два или более двух делителей.

Теорема.Наименьший, отличный от 1, делитель целого числа, большего единицы, есть число простое.

Доказательство:Пустьq- наименьший, отличный от 1, делитель натурального числаПредположим, что числоqсоставное, тогда оно имеет делитель. По свойству транзитивности– делитель числап, причем, что противоречит выбору числаq. Полученное противоречие говорит о том, что наше предположение неверно и числоqпростое. ■

Теорема.Простых чисел бесконечно много.

Доказательство:Предположим, что их конечное число и– все простые числа. Тогда числоотлично от 1 и от, т.е. составное, а значит оно делится хотя бы на одно простое число. ПустьТогдат.е.делит 1, а это неверно. Аналогично получим, чтоNне может делиться ни на одно другое простое число. Противоречие. ■

Упражнения и задачи

1. Доказать бесконечность числа простых чисел вида ,,,,,.

2. Если простое число то его можно представить в виде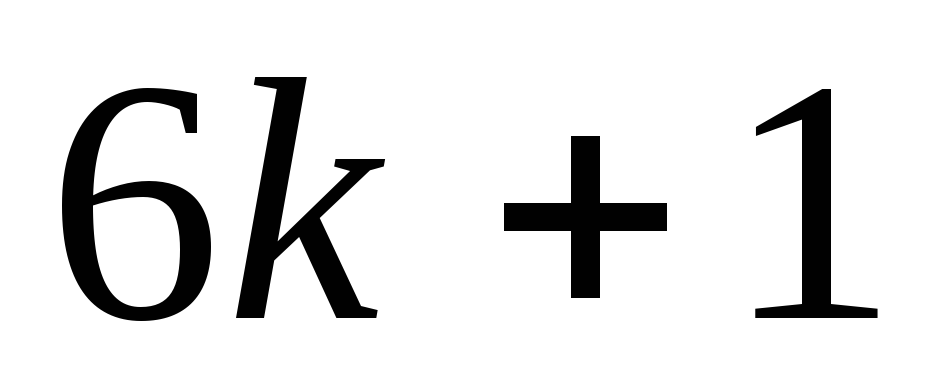илиДоказать.

3. Если p- простое число, тоделится на 24. Доказать.

4. Доказать, что при натуральном число составное

а) (теорема Софи Жермен); б)

5. Найти все простые числа p, для которых

а) итоже простые;

б) тоже простое.

6. Решить в простых числах

7. Если - простое число, то иn- простое число. Доказать.

8. Если - простое число, то числопявляется степенью числа 2. Доказать.

9. С помощью решета Эратосфена составить таблицу простых чисел, не превосходящих 500.

10. Доказать, что квадрат простого числа при делении на 30 дает в остатке 1 или 19.

11. Проверить, что значения при- простые числа.

12. Проверить, что значения простые при

13. Доказать, что не делится на 121 ни при какомп.

14. Наименьший простой делитель составного числа Nне превосходит. Доказать.

15. – количество простых чисел, не превосходящих действительного числа. Найти.