Упражнения и задачи

1. Найти корни уравнений:

а) б)

2. Доказать тождества:

а)

б)

3. Выразить в радикалах корни из 1 степеней 3, 4, 6, 8, 12.

4. Вычислить сумму s-xстепеней всех корней степенипиз 1, гдеs– целое число.

§1.2.9 Показательная форма записи комплексного числа

Пусть – действительное число. Полагаем

(1)

Эта формула называется формулой Л. Эйлера. Она не доказывается, а принимается в качестве определения символаТакое определение оправдано тем, что сохраняются основные свойства действительных показателей. Здесье– основание натуральных логарифмов,. Для любого комплексного числавновь полагаем:

(2)

Эта формула не приведет к противоречию в случае, когда z– действительное число, со свойствами возведения действительного числа в действительную степень.

Основные свойства возведения в комплексную степень:

1. 

2. 

3. 

С помощью формулы Эйлера комплексное число можно записать в показательной форме:

(3)

где r– модуль числаz, а– его аргумент. При этом формула Муавра принимает вид:

Корни п-ой степени из числаzполучают вид:

Замена нав формуле Эйлера дает формулу:

Отсюда легко получаем

Пример.Выразить через косинусы углов кратныха)б)

Решение:а)

б)

Упражнения и задачи

Определить вид кривых, заданных следующими уравнениями:

1. 

2. 

3. 

4. 

5. 

Контрольная работа №2 по теме “Комплексные числа”

I вариант

1. Вычислите:

а) (2 + 5i )³; б).

2. Решите уравнение: .

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а) ; б).

4. Решите уравнение: а) ; б).

5. Пусть , где. Докажите, чтоw– чисто мнимое тогда и только тогда, когда.

6. Изобразите на плоскости множество всех точек, для которых

7. Выразите через тригонометрические функции кратных углов.

8. Найдите сумму:

.

II вариант

1. Вычислите:

а) ; б).

2. При каких комплексных zвыраженияи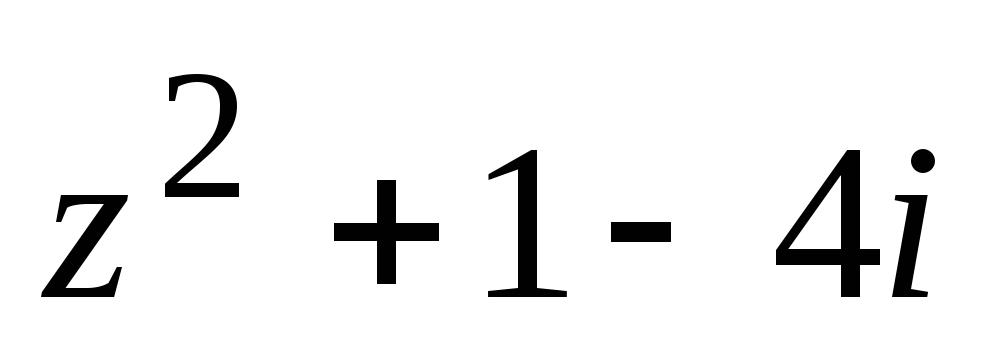одновременно имеют действительные значения?

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а) ; б).

4. Решите уравнение: а) ; б).

5. Для каких целых n?

6. Изобразите на плоскости множество всех точек, для которых

7. Выразите через.

8. Найдите сумму:

.

III вариант

1. Вычислите:

а) б).

2. При каких действительных xиyчислаибудут комплексно сопряженными?

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а) ; б).

4. Решите уравнение: а) ; б).

5. Вычислите z¹⁹⁷¹+, если.

6. Изобразите на плоскости множество всех точек, для которых

7. Выразите 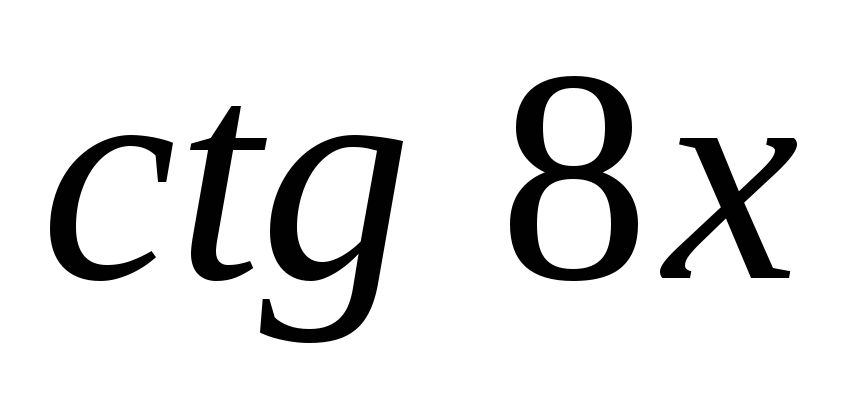через.

8. Найдите сумму:

.

IV вариант

1. Вычислите:

а) б).

2. Найдите действительные значения x, при которых комплексные числаи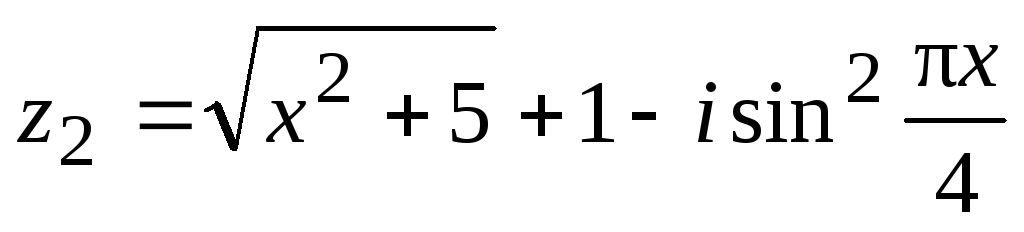являются сопряженными.

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а) ; б).

4. Решите уравнение: а) б).

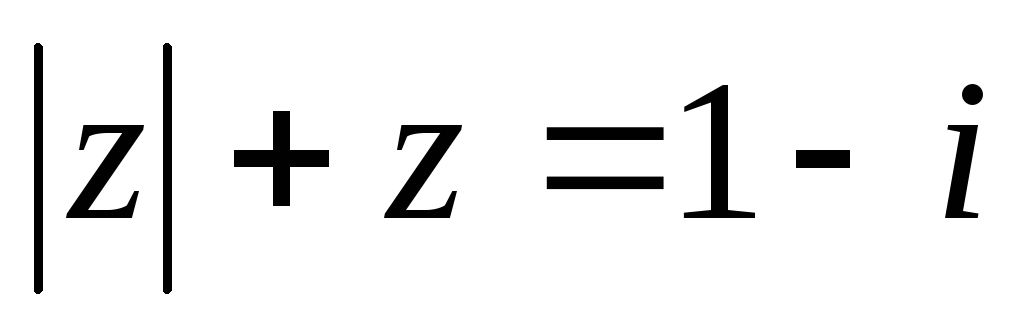5. Вычислите z¹⁹⁷¹+, если.

6. Изобразите на плоскости множество всех точек, для которых

7. Выразите через.

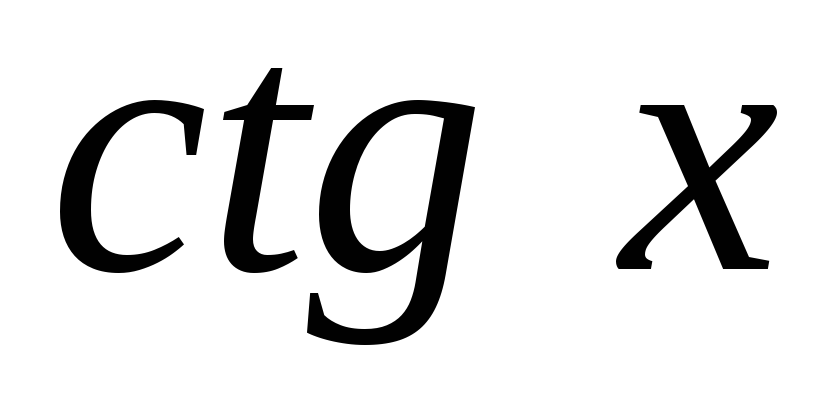8. Найдите сумму:

.

V вариант

1. Вычислите:

а) ; б).

2. При каких действительных хиучислаибудут комплексно сопряженными?

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а) ; б).

4. Решите уравнения: а) 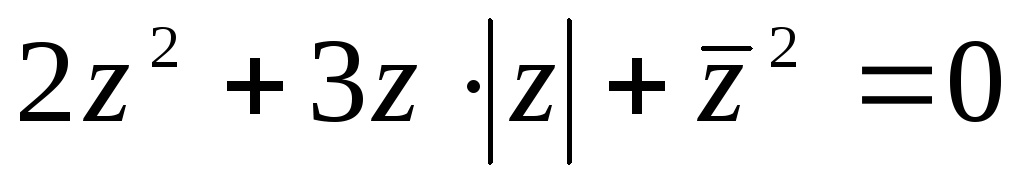; б).

5. Докажите, что а) ; б); в).

6. Изобразите на плоскости множество всех точек, для которых

7. Выразить через.

8. Найдите сумму:

.

VI вариант

1. Вычислите: а) ; б).

2. Решите уравнение: .

3. Вычислите, используя тригонометрическую форму записи:

а) ; б).

4. Решите уравнения: а) ; б).

5. Докажите, что а) ; б); в).

6. Изобразите на плоскости множество всех точек, для которых

7. Выразите через.

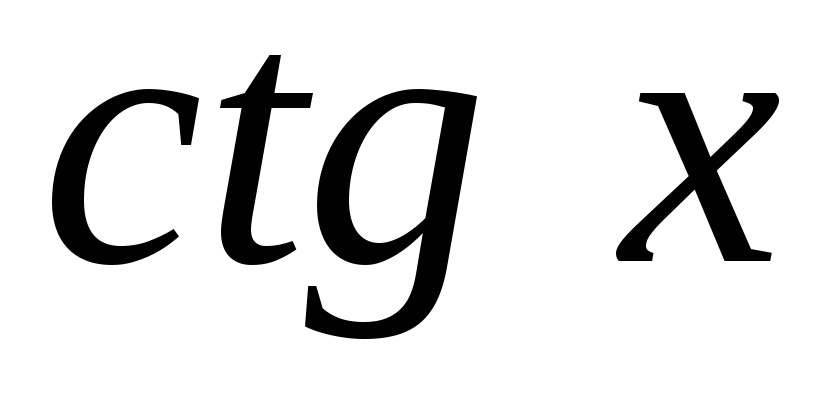8. Найдите сумму: .

VII вариант

1. Вычислите: а) ; б).

2. Решите уравнение: .

3. Вычислите, используя тригонометрическую форму записи:

а) ; б).

4. Решите уравнения: а) ; б).

5. Если – корень многочлена с действительными коэффициентами, то и число, сопряженное числу, также корень этого многочлена. Докажите это.

6. Изобразите на плоскости множество всех точек, для которых

7. Выразите через.

8. Найдите сумму: .

VIII вариант

1. Вычислите: а); б).

2. Решите уравнение: .

3. Вычислите, используя тригонометрическую форму записи:

а) ; б).

4. Решите уравнения: а) ; б).

5. Если – действительные число, то, где. Докажите это.

6. Изобразите на плоскости множество всех точек, для которых

7. Выразите через.

8. Найдите сумму: .

IX вариант

1. Вычислите: а); б) .

2. Найдите, при каких комплексных значениях k уравнение.

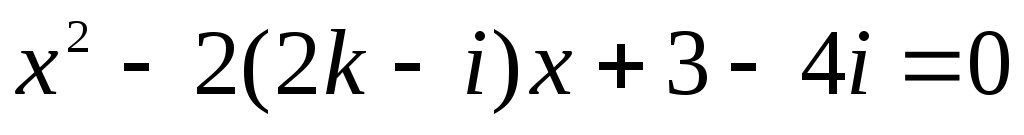3. Вычислите, используя тригонометрическую форму записи:

а) ; б).

4. Решите уравнения: а) ; б).

5. Докажите, что , если,

6. Изобразите на плоскости множество всех точек, для которых

7. Выразите через.

8. Найдите сумму: .

X вариант

1. Вычислите: а) ; б).

2. Решите уравнение: .

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а) ; б).

4. Решите уравнения: а) , б).

5. Докажите свойства модуля комплексного числа:

а) , б).

6. Изобразите на плоскости множество всех точек, для которых

7. Выразите через тригонометрические функции кратных углов.

8. Найдите сумму: .

XI вариант

1. Вычислите: а)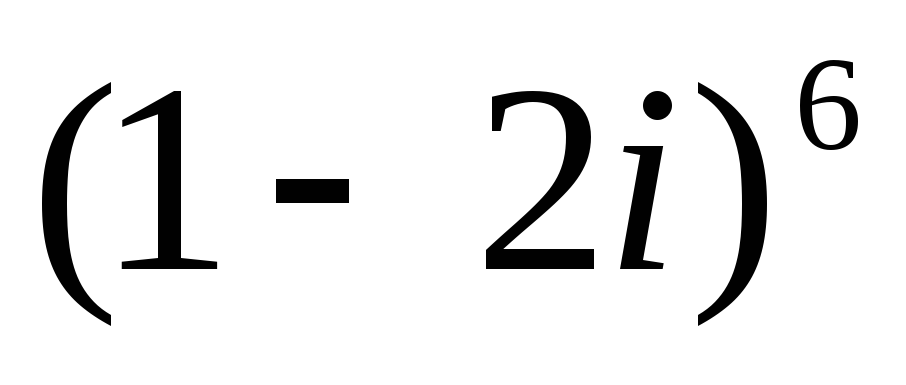; б).

2. Решите уравнение: .

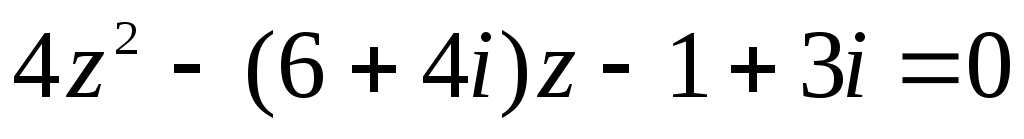3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а), б).

5. Докажите свойства модуля комплексного числа:

а), б).

6. Изобразите на плоскости множество всех точек, для которых

7. Выразите через.

8. Найдите сумму: .

XII вариант

1. Вычислите: а); б).

2. Решите уравнение: .

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а) б)

4. Решите уравнения: а), б).

5. Докажите, что если комплексное число удовлетворяет соотношению, то наибольшее возможное значение его модуля равно.

6. Изобразите на плоскости множество всех точек, для которых

7. Выразите через.

8. Докажите, что .

XIII вариант

1. Вычислите: а); б).

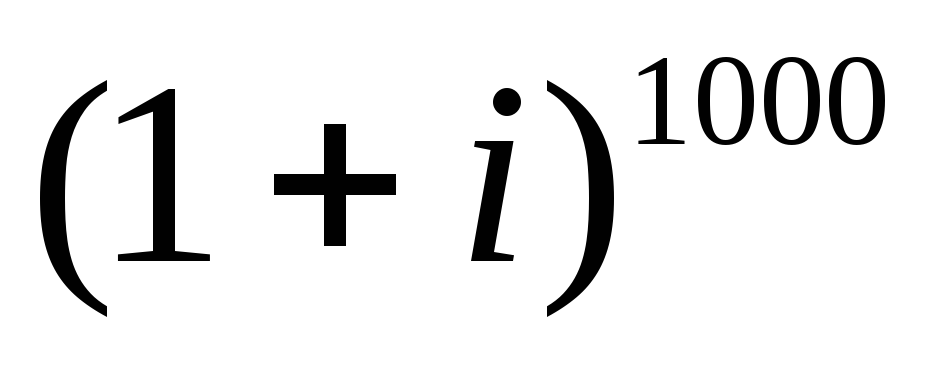2. Решите уравнение: .

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а)б)

4. Решите уравнения: а), б).

5. Вычислите выражение , еслиесть корень уравнения.

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите 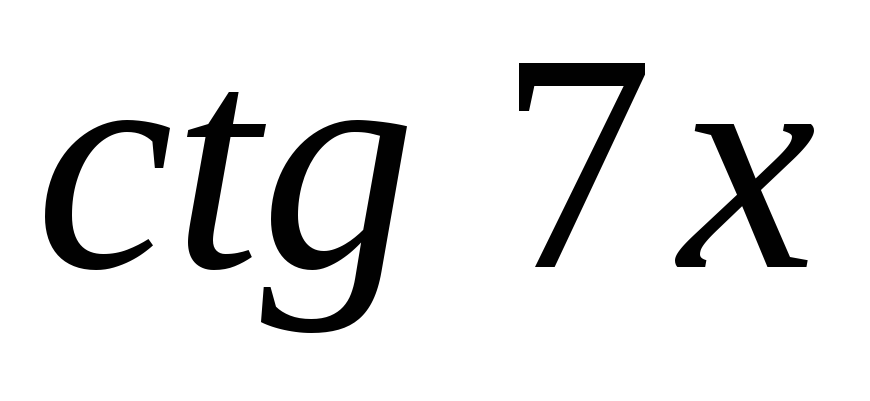через.

8. Докажите, что .

XIV вариант

1. Вычислите: а); б).

2. Решите уравнение:.

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а)б)

4. Решите уравнения: а), б).

5. Пусть . Докажите, чтоитогда и только тогда, когда, где.

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите через.

8. Найдите сумму .

XV вариант

1. Вычислите: а); б).

2. Решите уравнение:.

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а)б)

4. Решите уравнения: а), б).

5. Пусть . Докажите, чтоитогда и только тогда, когда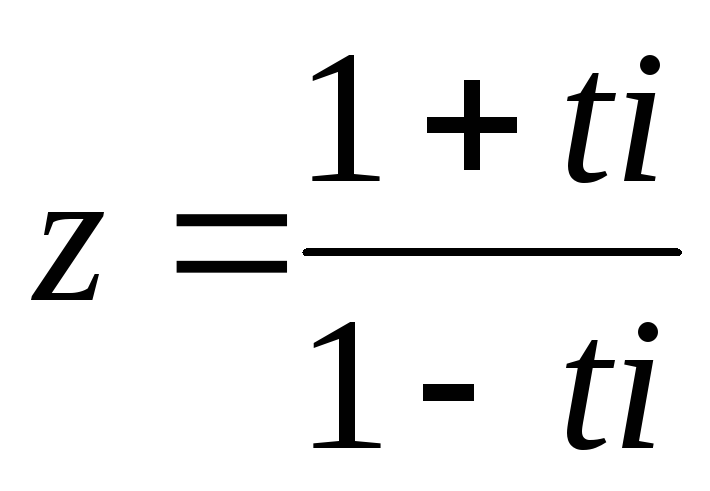, где.

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите через.

8. Докажите, что .

XVI вариант

1. Вычислите: а); б).

2. Найдите, при каких комплексных значениях kуравнениеимеет разные корни.

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а) ; б)

4. Решите уравнения: а), б).

5. Докажите, что .

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите через.

8. Найдите сумму: .

XVII вариант

1. Вычислите: а); б).

2. Найдите все комплексные числа хиутакие, что числаx, 2x+y, 2x+yобразуют арифметическую прогрессию, а числаобразуют геометрическую прогрессию.

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б)

4. Решите уравнения: а), б).

5. Выясните, при каких условиях произведение двух комплексных чисел а)чисто мнимое число, б) вещественное число.

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите через.

8. Докажите, что .

XVIII вариант

1. Вычислите: а); б).

2. Найдите все числа, сопряженные своему квадрату

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а)б)

4. Решите уравнения: а), б).

5. Докажите, что .

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите через.

8. Докажите, что:

.

XIX вариант

1. Вычислите: а); б).

2. Найдите все числа, сопряженные своему кубу.

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а), б).

5. Докажите, что .

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите через тригонометрические функции кратных углов.

8. Докажите, что:

.

XX вариант

1. Вычислите: а); б).

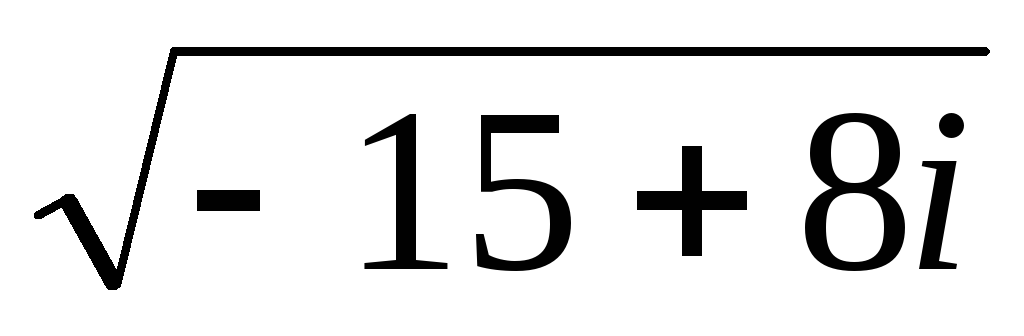2. Решите систему, считая, что x, y, z, tвещественные:

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а), б).

5. Упростите выражение: .

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите через тригонометрические функции кратных углов.

8. Докажите, что.

XXI вариант

1. Вычислите: а)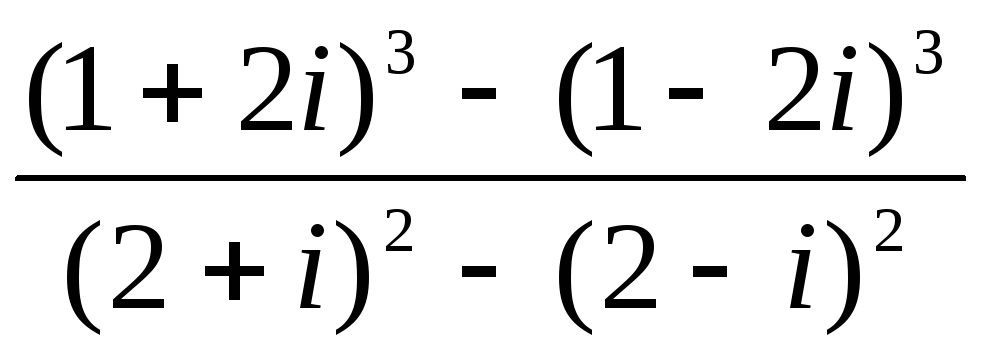; б).

2. Решите систему:

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а)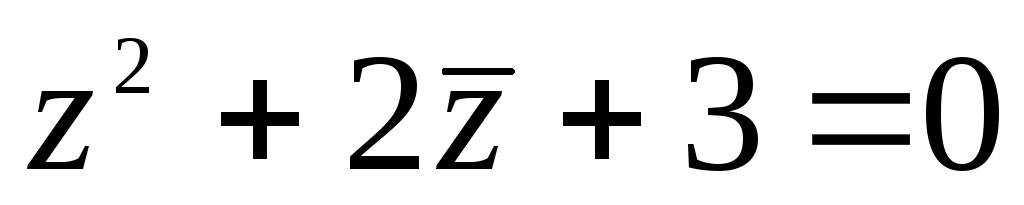, б).

5. Докажите равенство: .

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите через тригонометрические функции кратных углов.

8. Докажите, что.

XXII вариант

1. Вычислите: а); б).

2. Решите систему: .

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а)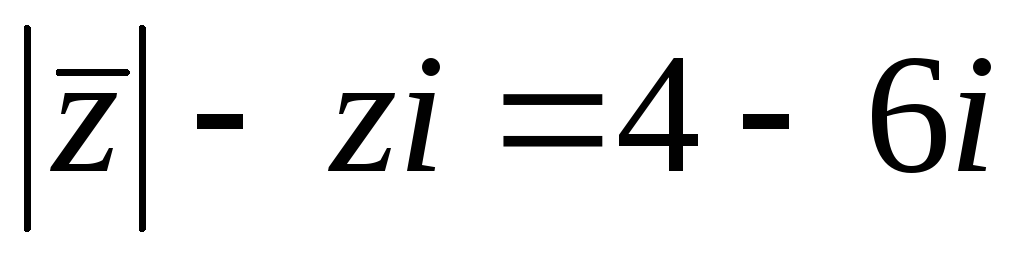, б).

5. Докажите, что икомплексно сопряженные тогда и только тогда, когда+и– действительные числа.

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите черези.

8. Найдите сумму: .

XXIII вариант

1. Вычислите: а); б).

2. Решите систему: .

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а), б).

5. Докажите равенство: .

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите черези.

8. Найдите сумму: .

XXIV вариант

1. Вычислите: а); б).

2. Решите уравнение: .

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а), б).

5. Докажите, что корни уравнения могут быть записаны в виде.

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите черези.

8. Найдите сумму: .

XXV вариант

1. Вычислите: а); б).

2. Решите уравнение: .

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а), б).

5. Найдите сумму p-x степеней корней уравнения, гдеp– целое.

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите черези..

8. Найдите сумму:.

XXVI вариант

1. Вычислите: а); б).

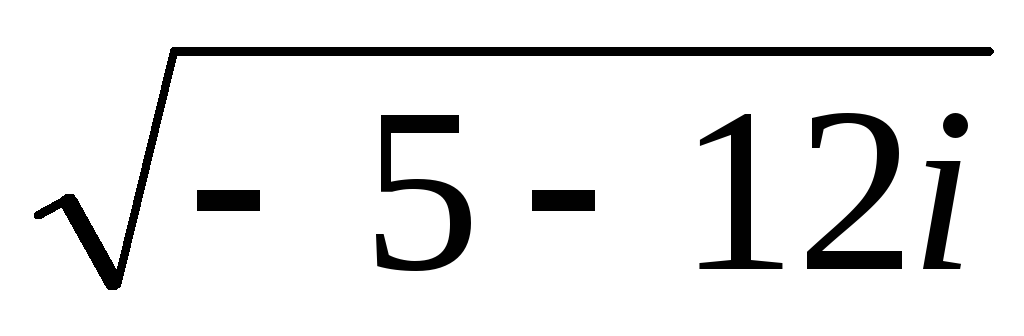2. Решите систему:

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а), б).

5. Докажите, что , если.

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите черези..

8. Найдите сумму: .

XXVII вариант

1. Вычислите: а); б).

2. Решите систему:

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а), б).

5. Где расположены точки на числовой плоскости, для которых (z– комплексное число)?

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите черези..

8. Найдите сумму: .

XXVIII вариант

1. Вычислите: а)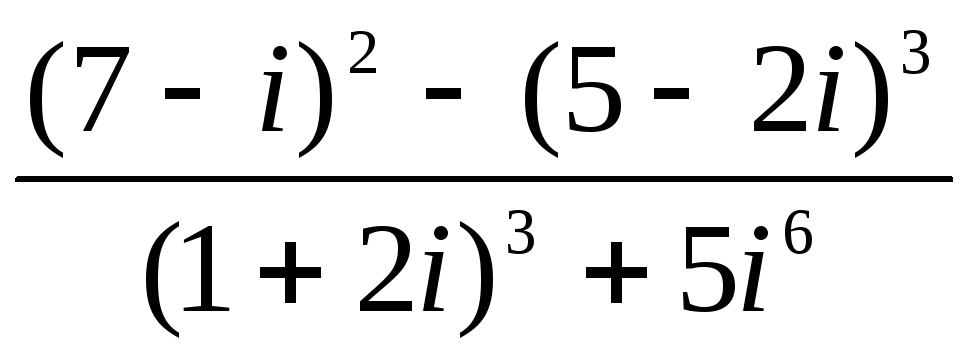; б).

2. Решите систему:

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а), б).

5. Найдите порядки всех корней из единицы 12 степени.

6. Изобразите на плоскости множество всех точек, для которых.

7. Выразите черези.

8. Найдите сумму: .

XXIX вариант

1. Вычислите: а); б).

2. Решите систему:

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а), б).

5. Докажите, что если – первообразный кореньn-той степени из 1, то и– первообразный кореньn-той степени из 1.

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите черези.

8. Найдите сумму: .

XXX вариант

1. Вычислите: а); б).

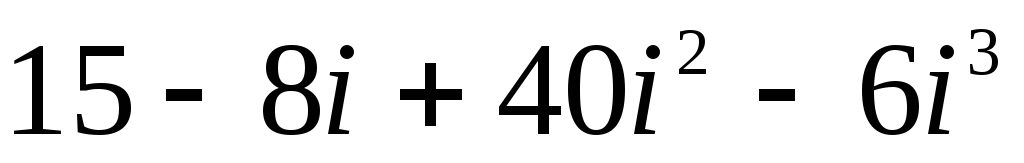2. Решите уравнение: .

3. Вычислите, используя тригонометрическую форму записи комплексного числа:

а); б).

4. Решите уравнения: а), б).

5. Найдите порядки всех корней из 1 степени 20.

6. Изобразите на плоскости множество всех точек, для которых .

7. Выразите через.

8. Найдите сумму: .