§1.2.6 Модуль комплексного числа

Напомним некоторые свойства модуля комплексного числа:

1. если

2. 

3. 

4. 

5. 

6. 

Теорема:(Неравенство треугольника: сумма двух сторон треугольника не меньше его третьей стороны).

Доказательство:ТогдаОтсюдат.е.■

Пример.Доказать, что

Доказательство:Аналогично,

Пример.a,b– комплексные числа. Если– вещественное положительное число, тоДоказать это.

Доказательство:

Упражнения и задачи

1. При каком условии точка лежит внутри круга радиусаRи центром в точке

2. Доказать равенства:

а)

б)

3. Доказать, что если 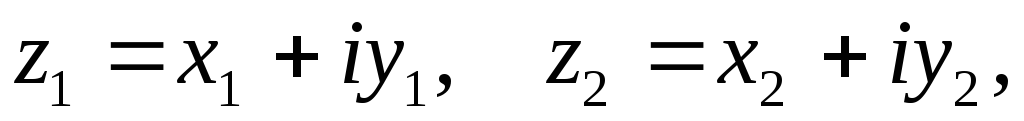то

4. Доказать, что уравнения с вещественными коэффициентами

не могут иметь корней, больше единицы по модулю.

5. Решить уравнение:

а) б)

§1.2.7 Извлечение корня из комплексного числа

Число называетсякорнем п-ой степенииз комплексного числаz, еслиНапример, числа -i,iявляются корнями второй степени из числа -1, так какЕслиz= 0, то– единственный кореньп-ой степени.

Теорема.Для любого комплексного числасуществует ровнопкорнейп-ой степени, которые определяются по формуле:

Доказательство:ПустьТогда

Отсюда

Возведя обе части каждого равенства в квадрат и сложив полученные равенства, получим:

(арифметический корень).

Из условия имеем

т.е.

■

Для k= 0, 1, 2, 3,...,п-1 получаются различные значения чисела для каждого из остальных значенийбудет получаться одно из этих чисел.

Отсюда следует, что все числа имеют равные модулино различные главные аргументы, отличающиеся друг от друга на величинуЧисла, следовательно, соответствуют точкам комплексной плоскости, расположенным в вершинах правильногоп-угольника, вписанного в круг радиусас центром в начале координат.

Пример.Найти все корни четвертой степени из числа 16i.

Решение:Посколькуто применяя формулу для извлечения корней, получаем

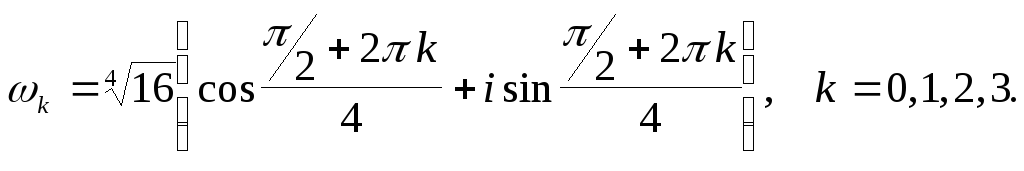
Следовательно,

Пример.Вычислить

Решение: ПустьТогдат.е.ЕслитоЕслито

Ответ:

Упражнения и задачи

1. Вычислить квадратные корни из чисел:

а) б)в)

2. Найти все значения следующих корней:

а) б)в)г)

3. Найти:

а) б)

4. Решить уравнение:

а) б)в)г)д)

§1.2.8 Корни из 1

По формулам извлечения корней все пкорнейп-ой степени из 1 можно записать в виде:

т.е. все они являются степенями одного корня

Теорема.Множествовсех корней из 1 образуют мультипликативную группу.

Доказательство:ПустьТогдат.е. множествозамкнуто относительно умножения, выполняется и аксиома ассоциативности (она выполняется для всех комплексных чисел, а, следовательно, и для корней из 1). Так както это множество содержит нейтральный элемент относительно умножения. Ясно, что еслитотакже, т.е. для любого элементаизэлементтоже принадлежит этому множеству. ■

Теорема.Множествовсех корнейп-ой степени из 1 образуют конечную мультипликативную группу.

Доказывается аналогично предыдущей теореме. ■

Пример.Найти все корни третьей степени из 1.

Решение:Поэтому

Все корни п-ой степени из 1 изображаются точками, лежащими на окружности радиуса 1 с центром вОи делящими эту окружность направных частей.

Пример.Доказать тождество

Доказательство:Это уравнение имееткорней, корней из 1, т.е. его корни:

Пример.Найти сумму всех корнейп-ой степени из 1.

Решение:ПустьТогда все корнип-ой степени из 1 можно представить в видеОтсюда сумма всех корней равна

Ответ:0.

Пример.Найти произведение всех корнейп-ой степени из 1.

Решение:Разобьем все сомножители, отличные от 1 и -1, на пары взаимно обратных чисел. Произведение чисел каждой пары равно 1. Еслипчетно, то все произведение равно 1, а еслипнечетно, то -1.

Ответ: