
- •Модуль 1. Элементы теории чисел Глава 1.1. Целые числа §1.1.1. Теория делимости
- •Упражнения и задачи
- •§1.1.2 Наибольший общий делитель. Алгоритм Евклида
- •Упражнения и задачи
- •§1.1.3 Теорема о линейном представлении наибольшего общего делителя
- •Упражнения и задачи
- •§1.1.4 Наименьшее общее кратное
- •Упражнения и задачи
- •§1.1.5 Простые числа
- •Упражнения и задачи
- •§1.1.6 Основная теорема арифметики кольца целых чисел
- •Упражнения и задачи
- •§1.1.7 Целая часть числа
- •Упражнения и задачи
- •§1.1.8 Функция Эйлера
- •Упражнения и задачи
- •§1.1.9 Сравнения
- •Упражнения и задачи
- •§1.1.10 Полная система вычетов
- •Упражнения и задачи
- •§1.1.11 Приведенная система вычетов
- •Упражнения и задачи
- •§1.1.12 Теорема Эйлера
- •Упражнения и задачи
- •§1.1.13 Кольцо классов вычетов
- •Упражнения и задачи
- •§1.1.14 Решение сравнений
- •Упражнения и задачи
- •Контрольная работа №1 по теме “Целые числа”
- •I вариант
- •II вариант
- •III вариант
- •IV вариант
- •V вариант
- •VI вариант
- •VII вариант
- •VIII вариант
- •IX вариант
- •X вариант
- •XI вариант
- •XII вариант
- •XIII вариант
- •XIV вариант
- •XV вариант
- •XVI вариант
- •XVII вариант
- •XVIII вариант
- •XIX вариант
- •XX вариант
- •XXI вариант
- •XXII вариант
- •XXIII вариант
- •XXIV вариант
- •XXV вариант
- •XXVI вариант
- •XVII вариант
- •XXVIII вариант
- •XXIX вариант
- •XXX вариант
- •Глава 1.2. Комплексные числа и комплексные функции
- •§1.2.1 Алгебраическая форма комплексного числа
- •Упражнения и задачи
- •§1.2.2 Комплексно сопряженные числа
- •Упражнения и задачи
- •§1.2.3 Геометрическая интерпретация комплексных чисел
- •Упражнения и задачи
- •§1.2.4 Тригонометрическая форма комплексного числа
- •Упражнения и задачи
- •§1.2.5 Формула Муавра
- •Упражнения и задачи
- •§1.2.6 Модуль комплексного числа
- •Упражнения и задачи
- •§1.2.7 Извлечение корня из комплексного числа
- •Упражнения и задачи
- •§1.2.8 Корни из 1
- •Упражнения и задачи
- •§1.2.9 Показательная форма записи комплексного числа
- •Упражнения и задачи
Модуль 1. Элементы теории чисел Глава 1.1. Целые числа §1.1.1. Теория делимости
Целыми называются числа ..., -3, -2, -1, 0, 1, 2, 3,..., т.е. натуральные числа 1, 2, 3, 4,..., а также нуль и отрицательные числа -1, -2, -3, -4,.... Множество всех целых чисел обозначается черезZ(от немецкого словаZahl– число).
Сумма, разность и
произведение двух целых чисел – также
целые числа. Если для трех целых чисел
a, bисвыполнено равенство![]() то говорят:а делится на bилиb делит аи
применяют соответственно обозначения
то говорят:а делится на bилиb делит аи
применяют соответственно обозначения![]() При этоманазываюткратным числа
b, аb–делителем числа а.
При этоманазываюткратным числа
b, аb–делителем числа а.
Свойства делимости целых чисел:
аделится наа(рефлексивность);
если аделится наb,bделится наа, то
 или -b;
или -b;если аделится наb,bделится нас, тоаделится нас(транзитивность);
если
 аделится наd,bделится наd, то исделится наd;
аделится наd,bделится наd, то исделится наd;если adделится наbd,
 тоаделится наb.
тоаделится наb.
Доказательствосвойства 1:![]()
Доказательствосвойства 2:![]() Отсюда
Отсюда![]() т.е.
т.е.![]()
![]() или -1.
или -1.
Доказательствосвойства 3:![]() Отсюда
Отсюда![]()
Доказательствосвойства 4:![]() Отсюда
Отсюда![]()
Доказательствосвойства 5:![]() Отсюда
Отсюда![]()
Теорема (о делении с остатком): Для любых двух целых чиселаиbсуществует и притом единственная пара чиселqиr, для которых
![]() .
.
Доказательствотеоремы существования. Расположим на числовой оси числа ..., -2b, -b, 0,b, 2b,...

Они разбивают ось на
интервалы длины
![]() в один из которых попадает числоа,
т.е. существует целое числоq,
для которого
в один из которых попадает числоа,
т.е. существует целое числоq,
для которого
![]()
Введем обозначение
![]() Тогда
Тогда
![]()
Доказательство теоремы единственности проведем методом от противного. Пусть существуют два представления
![]() (1)
(1)
![]() (2)
(2)
Предположим, что
![]() Тогда
Тогда![]() Здесь
Здесь![]() в то же время
в то же время![]()
![]() Получили
противоречие, а это значит, что
предположение
Получили
противоречие, а это значит, что
предположение![]()
![]() неверно.
Аналогично приводит к противоречию
предположение
неверно.
Аналогично приводит к противоречию
предположение![]() Остается лишь одна возможность
Остается лишь одна возможность![]() но тогда и
но тогда и![]() т.е. оба представления совпадают.
т.е. оба представления совпадают.
Доказательство закончено. ■
Число qв равенстве![]() называетсянеполным частным, аrостатком от деления анаb.
Если
называетсянеполным частным, аrостатком от деления анаb.
Если![]() тоqназываетсячастнымот деления анаb.
тоqназываетсячастнымот деления анаb.
Пример.Если![]() то
то![]()
Если
![]() то
то![]()
Если
![]() то
то![]()
Если
![]() то
то![]()
Если
![]() то
то![]()
Упражнения и задачи
Если каждое из чисел аиbделится нас, то их сумма и разность также делится нас. Доказать.
Для любого целого числа bеслиаделится нас, то иabделится нас. Доказать.
Если
 то
то Доказать это.
Доказать это.Если аделится наb, то при любом целом
 иakделится наbkиakделится наb.
Доказать.
иakделится наbkиakделится наb.
Доказать.Если аделится наb, то при любом целом
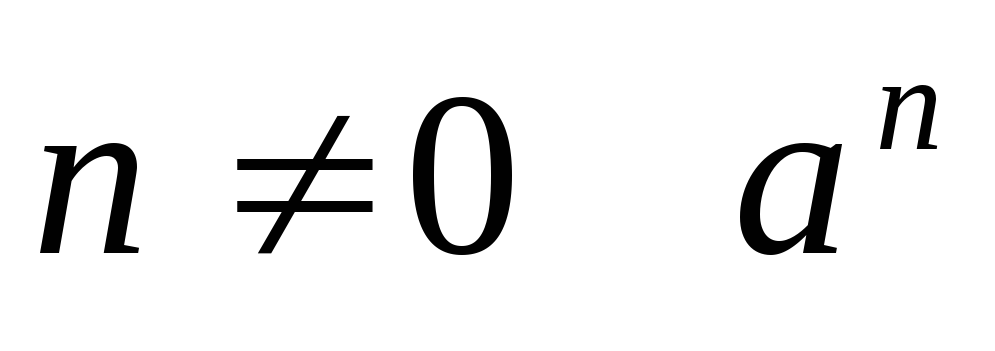 делится на
делится на Доказать.
Доказать.Для любых целых чисел
 и
и существует и притом единственное
представление числаав виде
существует и притом единственное
представление числаав виде где
где при всех
при всех (представление числаав системе
счисления с основаниемт). Доказать.
(представление числаав системе
счисления с основаниемт). Доказать.Произведение трех последовательных целых чисел делится на 6. Доказать.
Произведение четырех последовательных целых чисел делится на 24. Доказать.
Доказать, что
 делится на 30 для любого целого числат.
делится на 30 для любого целого числат.Доказать, что:
а) если
![]() делится на 3, тоаделится на 3 иbделится на 3;
делится на 3, тоаделится на 3 иbделится на 3;
б) если
![]() делится на 7, тоаиbтоже делятся на 7;
делится на 7, тоаиbтоже делятся на 7;
в) если
![]() тоabcделится на 60.
тоabcделится на 60.
Найти шестизначное число, которое оканчивается на 5 и увеличивается в 4 раза после перестановки этой цифры на первое место.
Если пятизначное число делится на 41, то и все числа, полученные путем круговой перестановки цифр этого числа, делятся на 41. Доказать это.
Если трехзначное число abcделится на 37, то и числаbca, cabтоже делятся на 37. Доказать.
Если
 делится на
делится на то и
то и делится на
делится на Доказать.
Доказать.Найти четырехзначное число, которое при делении на 251 и 252 дает в остатке 209 и 202.
Вывести признаки делимости на 2, 3, 4, 5, 6, 10, 11, 12, 14, 15, 25, 125.
