Длинные линии

VI. Режим смешанных волн. А) Линия с активным сопротивлением нагрузки.

При нагрузке активного или комплексного характера отраженная волна будет иметь меньшую амплитуду, чем падающая. Положим, что имеетсялиния без потерь, нагруженная на(рис. 103) причем, тогда коэффициент отражениявещественен. (рисунок 103В этом случае уравнения (182) припринимают

вид: (190), где;Рис.103

Отсюда для действительных амплитуд напряжения и тока имеем:

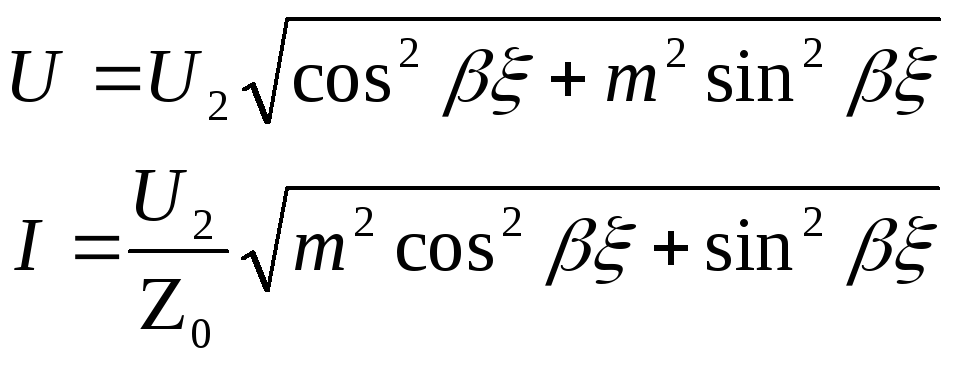(191)

Пусть m<1, т.е. >. Получающиеся при этом графики распределения амплитуд напряжения и тока вдоль линии, показаны на рисунке 104. Из рисунка 104 видно, что максимум напряжения и минимум тока наблюдается при

, а минимум напряжения и максимум тока наблюдается при

Из (191) следует, что в этих точках величины напряжения и тока:

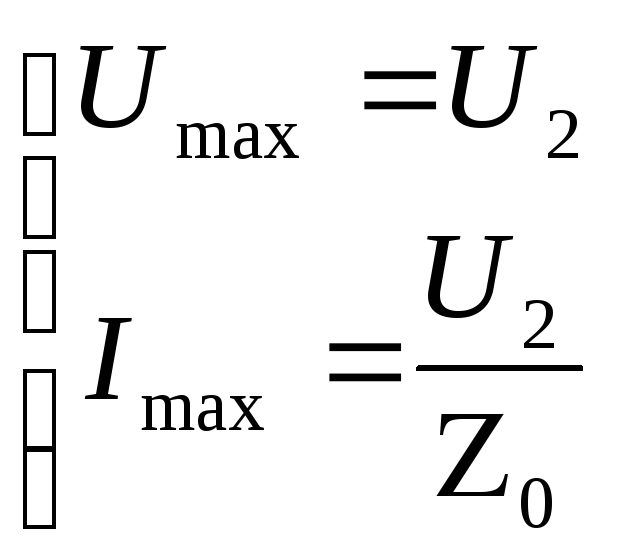
(192)

При и. Это означает, что смешанные волны в данном случае

Рис.104 Распределение амплитуд апряжения и тока вдоль линии.

вырождаются в стоячие, наблюдаемые в линии, разомкнутой на конце.

На рисунке 105 представлены графики распределения амплитуд UиIдляm>1

(т.е. <).

Нетрудно показать, что при m>1:

и(193)

При и, т.е. снова образуются

стоячие волны. При m=1

наблюдается режим бегущих волн.

В общем случае смешанную волну

можно представить в виде совокупности бегущей

и стоячей волн.

Этим, собственно, и объясняется

термин “смешанная волна".

Рис.105 Распределение амплитуд

напряжения и тока для m>1.

Для характеристики процессов в длинной

линии вводится так называемый

коэффициент бегущей волны [ЛБВ].

- реальная величина.

Если линия нагружена на активное сопротивление, то как следует из (192) и (193):

; при

; при

Установим связь между коэффициентами бегущей волны и коэффициентом отражения. Учитывая, что , и, имеем:

(194)

Наряду с в практике иногда применяют обратную ему величину-коэффициент стоячей волны.

;

Рассчитаем входное сопротивление линии, нагруженной на активное сопротивление. Используя(186) при имеем:

;

Освободившись от комплексности в знаменателе, будем иметь:

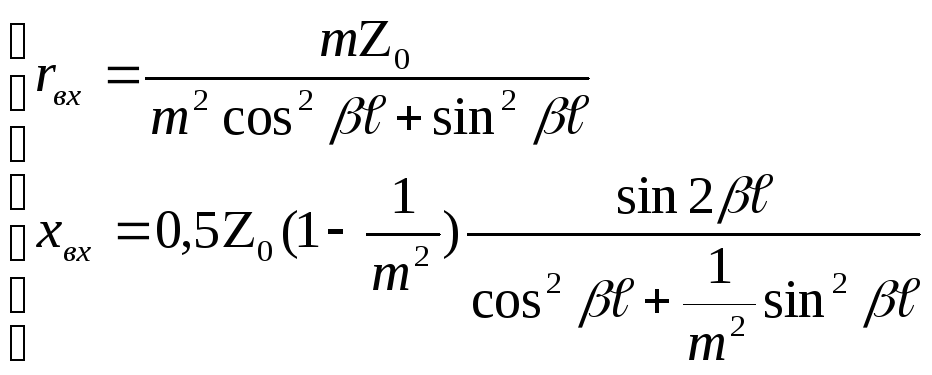(195) и (196)

Ход этих зависимостей для m=0,2

показан на рисунке 106 (т.е. ).В случаеэти же кривые сместятся вправо на

Рис.106 Линия, нагруженная на комплексное сопротивление.

Как было показано выше, входное сопротивление линии, нагруженной на активное сопротивление, в произвольной точке n=1,2,3,… имеет комплексный характер.

Если участок линии, расположенный справа от точки отбросить и вместо него включить новое сопротивление нагрузки, равное сопротивлению, то режим в оставшейся части линии не изменится. На основании этого можно утверждать, что при комплексной нагрузке в линии устанавливается режимсмешанных волн.Однако в отличии от активной нагрузки результирующие амплитуды тока и напряжения на конце линии теперь не имеют ни минимума, ни максимума.

Коэффициент отражения, как видно из (180)

(197)

где

Найдём координаты точек, где сдвиг фаз равен нулю так что результирующая

амплитуда будет достигать максимума. Для этого рассмотрим (178) с учётом (180) и (197) . В результате для линии без потерь будем иметь

;

Амплитуда будет максимальная, и если ;

Первый максимум находится в точке

; (198)

Используя (194) и (199) найдём КБВ (модуль подставим в 194)

Выражения (198) и (199) позволяют вычислить активную и реактивную составляющие сопротивления нагрузки , если известны волновое сопротивление, КБВ в линии и расстояние от ее конца до первого максимума (или минимума) напряжения (измерительной линии!).

Различием линии, длина которой равна. Из (184) (для линии без потерь) следует, чтов точках где.n=0,1,2…

Если n=2m;m=1,2,3… то,и согласно (186). При нечетныхn=2m-1 величинаи(200) равна нечеткому числу четвертей волны, осуществляет трансформацию сопротивлений.

VII. Согласование линии с нагрузкой.

Для отдачи максимальной мощности в нагрузку необходимо чтобы КБВ=1. Это имеет место если линия согласована как со входа, так и с выхода. Рассмотрим различные типы согласований.

109а 108 107 109б

Пусть волновое сопротивление линии равно , а сопротивление нагрузкичисто активно, причем. Расчет согласующего трансформатора в этом случае сводится к определению его волнового сопротивления. Последнее должно быть выбрано так, чтобы входное сопротивлениетрансформирующего отрезка с нагрузкойбыло равно величине. Используя (200) будем иметь:,откуда; (см. рис. 107). Если нагрузка комплексна, согласующий трансформатор следует включить на расстоянииот конца линии в точке, где входное сопротивление становится чисто активным (рис. 108). Волновое сопротивление трансформатора при этом должно быть, где- входное сопротивление отрезка линии длиной.

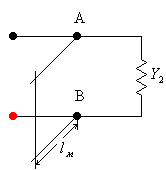
На практике чаще всего используется метод согласования описываемые ниже. Пусть линия с волновой проводимостью замкнута на комплексную проводимость. На некотором расстоянииот конца (рис.) активная составляющая входной проводимости равна волновой проводимости линии, а реактивная составляющая имеет какое-то значение, т. е. при. Если теперь между точками А и В включая реактивный элемент, проводимостью, то результирующая входная проводимость эквивалентного двухполюсника в этих точках примет вид:, тогда слева от точек А-В будет только падающая волна. В качестве реактивного элемента используют параллельный реактивный четвертьволновой отрезок линии, короткозамкнутой на конце (рис.). Волновое сопротивление его выбирается равным,аопределяется из условия:. Так как входная проводимость третьего отрезка линии равна. Поэтому необходимо, чтобы; откуда.

VIII Использование линий для задержки сигналов во времени и для создания линейных вольтметров

1). Задержка сигналов.

Т. к. фазовый сдвиг между колебаниями в точках линии отстоящих одна от другой на равно, то можно его записать так:, где[сек] или

Поскольку фазовый сдвиг линейно связан с частотой , то искажения формы импульса при его прохождении через линию не происходит , а поэтому линии без потерь используют для задержки сигналов во времени . Задержка в коаксиальных линиях мала исек/метр . В спиральных линияхсек.

Часто применяют искусственные линии задержки

Линия задержки представляет собой набор параллельно соединённых п-образных или т-образных фильтров .Поэтому увеличивая пользуясь формулой (200)^/ нельзя забывать

Что так что увеличиватьLС можно до определённых значений , елиLи С достигли предельных значений ,то увеличиваютза счёт дополнительного числа ячеек.

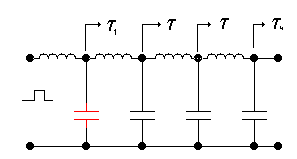
Рис(109).Искусственная линия задержки из п-образных или т-

образных фильтров

IX. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНИИ

1. Включение постоянного напряжения в разомкнутую линию

Допустим, что линия без потерь, имеющая длину , в момент . времениt= 0 подключена к источнику постоянного напряженияЕ. Под действием этого напряжения заряжается распределенная ем­кость линии, и в цепи течет постоянный ток. От генератора в линию распространяется волна напряженияЕи тока(рис. 9 а). Эту волну можно считать прямоугольной, так как каждая элементарная емкость заряжается до напряженияЕмгно­венно. По мере перемещения волны к концу линии элементы верх­него провода один за другим приобретают некоторый положитель­ный заряд, а от соответствующих элементов нижнего провода отнимается такой же положительный заряд. Противоположные за­ряды элементов линии образуют электрическое поле между прово­дами. Возникновение электрического поля на каждом элементе линии сопровождается появлением тока и магнитного поля. Следова­тельно, линия запасает электромагнитную энергию. Энергия каж­дой единицы длины линии, по которой течет ток /о, состоит из элек­трической и магнитной энергии, т. е.

рис9 Распространение волн в разомкнутой линии при включении постоянного напряжения

рис9.Распространение волн в разомкнутой линии при включении постоянного напряжения

Значение электрической и магнитной энергии падающей волны равны между собой.

,

В момент времени волны напряженияЕи токадохо­дят до разомкнутого конца линии (рис. 9,б) и отражаются от него. Энергия на конце линии не потребляется, и потому отражен­ная волна равна падающей (коэффициент отражения равен еди­нице). Физически отражение объясняется следующим. Когда волна достигает конца линии, у фронта волны ток мгновенно спадает отдо нуля, и этот спад последовательно распространяется от конца линии к началу. Пока спад не достигает начала линии, ток генера­тораостается неизменным, т. е. энергия от генератора поступает в линию. При спаде тока отдо нуля энергия магнитного поля и поступающая в линию энергия превращаются в электрическую энер­гию, за счет чего напряжение на линии удваивается. Этот процесс удобно представлять как движение двух встречных волн — падаю­щей и равной ей отраженной. Сумма падающей и отраженной волн напряжения равна2Е,так как волна напряжения при отражении не изменяет знака. Сумма падающей и отраженной .волн тока равна нулю, так как направление тока при отражении изменяется на про­тивоположное (рис. 9, в)

В момент времени отраженная волна достигает гене­ратора. Ток во всей линии становится равным нулю, а напряже­ние удваивается (рис. 9, г). В линии оказывается запасенной электрическая энергия

,

равная энергии, доставленной источником за время распространения волны от генератора к концу линии и обратно, т. е. за время

Генератор поддерживает постоянное напряжение Е.Поэтому, как только отраженная волна доходит до генератора (), напряжение фронта волны мгновенно падает от2ЕдоЕ.Этот спад напряжения распространяется со скоростью о от генератора к концу линии (рис. 9, д ). Линия разряжается: ток в линии имеет на­правление, противоположное тому, которое было при заряде. На­копленная в линии энергия возвращается источнику. Спад напря­жения от2ЕдоЕможно представить как распространение от гене­ратора к концу линии волны напряжения( -Е }и тока (). В момент времениэта волна доходит до конца линии. Напряжение во всех точках линии в это время равноЕ,ток равен(рис. 9, е); половина энергии линии возвращена гене­ратору.

Как только волна —Е, достигает конца линии, ток на конце мгновенно спадает до нуля, и этот спад распространяется до-конца линии к генератору. Магнитный поток чезает, напряжение на ли­нии падает до нуля, и происходит разряд линии от конца к на­чалу (рис. 9,ж ). Этот процесс можно рассматривать как распро­странение от конца линии к началу отраженной волны -Е,.

В момент времени отраженная волна -Е,дости­гает генератора ( рис. 9,6); на этом заканчивается первый период и начинается второй, в котором указанные процессы повто­ряются, и т. д.