Учебник + задачник АП Ильиных

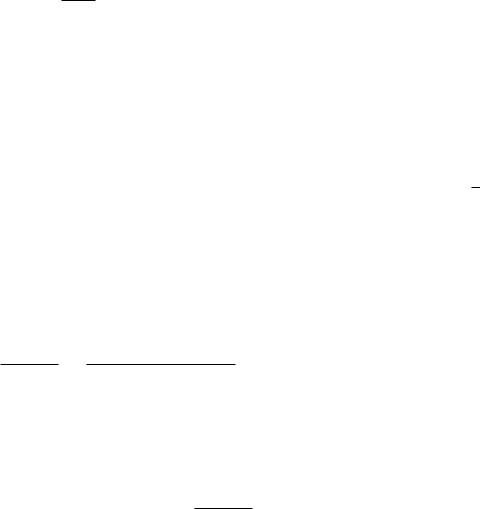
Продолжая процесс делений в алгоритме Евклида, для некоторого n получим

Мы имеем представление α в виде конечной дроби (11.2), и записываем α = [q1, q2, . . . , qn]. Теорема доказана.

ЗАМЕЧАНИЕ. Числа q1, q2, . . . , qn из конечной непрерывной дроби (11.2)– это неполные частные из алгоритма Евклида для чисел a и b.

Из теоремы следует, что иррациональные числа представляются в ви-

де бесконечной непрерывной дроби. Рассмотрим пример представления

√

в виде бесконечной непрерывной дроби иррационального числа α = 2. В соответствие с процессом представления нужно записать α = q1 + α0,

51

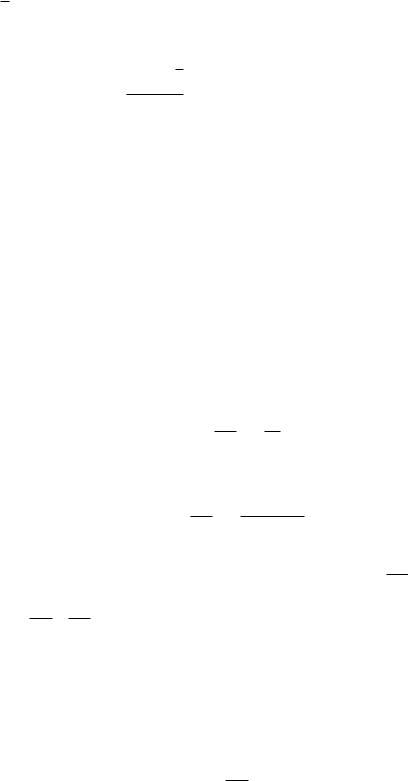
Периодичность непрерывной дроби означает, что последовательность неполных частных [q1, q2, q3, . . . ] начиная с некоторого номера образова-

на бесконечно повторяющейся группой чисел -периодом дроби. В случае

√

α= 2 имеем предпериод из числа 1 и наименьший период из числа 2. Назовем иррациональное число α квадратичной иррациональностью,

a + b, где a, b, c Z и b > 0. c

Справедливо следующее утверждение.

ТЕОРЕМА 11.2. Квадратичные иррациональности и только они представимы в виде периодической непрерывной дроби.

Доказательство в [11, стр. 191]. Наиболее сложно доказать, что произвольная квадратичная иррациональность представима в виде периодической непрерывной дроби. Это утверждение называется теоремой Лагранжа в честь французского математика и механика Ж. Лагранжа.

Свойства непрерывных дробей. Пусть число α представлено в виде конечной непрерывной дроби (11.2) или бесконечной дроби (11.3).

Отбросим в непрерывной дроби выражение, стоящие после q1. Полу-

чим дробь

P1 = q1 . Q1 1

Отбрасывая выражение после q2, имеем дробь

P2 = q2q1 + 1.

Q2 q2

Затем отбросим выражение после q3, получим дробь P3 и т.д.

Q3

Дроби P1 , P2 , . . . называются подходящими дробями для числа α.

Q1 Q2

Подходящую дробь с номером i можно записать с числителем Pi и знаменателем Qi, способ вычисления которых указан в последующем свойстве 1. При этом считаем, что

Дополнительно определим дробь P0 , где P0 = 1, Q0 = 0. Она потребует-

Q0

ся для единообразия формул.

52

СВОЙСТВО 1. Справедливо следующее правило вычисления чис-

Доказательство индукцией по числу i. Пусть i = 2. Нужно проверить, что

P2 = q2 · P1 + P0,

Q2 = q2 · Q1 + Q0.

Пусть утверждение верно для числа i. Тогда справедливы равенства (11.7) и (11.8). Проверим выполнение утверждения для числа i + 1, т.е.

жения Pi−1, Pi−2, Qi−1, Qi−2, то эти выражения не изменятся. Получаем

и равенства (11.9) и (11.10), что и нужно.

53

СВОЙСТВО 2. Для всех i > 1 справедливо равенство

Доказательство индукцией по i. Пусть i = 1. Имеем P1 · Q0 − P0 · Q1 = = q1 ·0−1·1 = −1, что и нужно. Пусть утверждение верно для числа i, т.е. верно равенство (11.13). Проверим истинность утверждения для числа i + 1, т.е. справедливость равенства

Pi+1 · Qi − Pi · Qi+1 = (−1)i+1.

По (11.9) и (11.10) имеем

Pi+1 · Qi − Pi · Qi+1 = (qi+1Pi + Pi−1) · Qi − Pi · (qi+1Qi + Qi−1) =

= Pi−1Qi − PiQi−1 = −(PiQi−1 − Pi−1Qi) = (−1)(−1)i = (−1)i+1,

что и нужно.

СВОЙСТВО 3. Подходящие дроби Pi несократимы.

Qi

Доказательство от противного. Пусть d = (Pi, Qi) и d > 1. Тогда d делит левую часть равенства Pi·Qi−1−Pi−1·Qi = (−1)i. Поэтому d делит правую часть (−1)i = ±1, противоречие, т.к. d > 1.

Получим теперь формулу для разности двух соседних подходящих дробей.

СВОЙСТВО 4. Для всех i > 1 справедливо равенство

Отсюда получаем расстояние между двумя соседними подходящими дробями

54

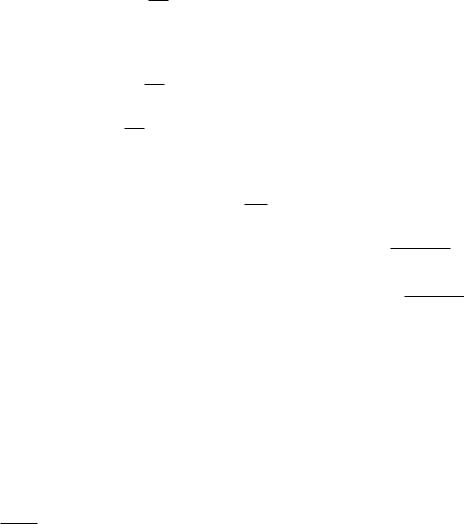
СВОЙСТВО 5. Пусть Pi подходящая дробь для числа α с номе-

Qi

ром i, отличная от последней дроби ( т.е. от самого числа α ). Тогда

1) Если i нечетно, то Pi < α.

Qi

2) Если i четно, то Pi > α.

Qi

Доказательство. В дроби (11.2) или (11.3) отбросим выражение > 0,

стоящее за q1. Полученное число, т.е. P1 меньше α. Отбросим выраже-

Q1

1

ние, стоящее за q2. При этом вместо выражения q2 + q3 + ... получим

1

меньшее число, что выражаем словами «выражения q2 + q3 + ... умень- шится». Тогда выражение

Из этого свойства следует, что число α заключено между соседними

Формула для решения сравнения первой степени. Используя подходящие дроби, получим удобную формулу для решения сравнения первой степени. Пусть дано сравнение

Если a < 0, то заменим сравнение (11.16) на равносильное сравнение (−a)x ≡ −b (mod m). Поэтому далее считаем, что a > 0.

55

ТЕОРЕМА 11.3 . Сравнение (11.16) имеет единственное реше-

где Pn−1 – числитель предпоследней подходящей дроби при разложении числа ma в непрерывную дробь.

Доказательство. Известно, что сравнение (11.16) имеет единственное

нение (11.18). Теорема доказана.

Решение в целых числах уравнения ax + by = c. Рассмотрим урав-

с неизвестными x, y и целыми коэффициентами a, b, c. Требуется найти целочисленные решения этого уравнения. Уравнение (11.19) называется неопределенным уравнением первой степени с двумя неизвестными. Применим теорию сравнений к решению неопределенных уравнений.

Заметим вначале, что при (a, b) = d > 1 и c 6... d уравнение (11.19) неразрешимо. Действительно, при наличии решения (x0, y0) имеем равенство ax0 + by0 = c. Левая часть ax0 + by0 этого равенства делится на d, а правая часть, равная c, не делится на d, противоречие.

Если (a, b) = d > 1 и c ... d, то a = a1d, b = b1d, c = c1d. Разделив на d уравнение (11.19), получим равносильное уравнение a1x + b1y = c1, где (a1, b1) = 1. Поэтому далее считаем, что (a, b) = 1.

Покажем способ для нахождения некоторого, первоначального решения (x0, y0) уравнения (11.19), а затем получим формулу для всех решений.

56

Перенесем by в уравнение (11.19) в правую часть. Получим ax = c−by. Поэтому

Так как (a, b) = 1, то сравнение имеет единственное решение. Рассмотрим

Предположим, что (x0, y0) – одно из решений этого уравнения. Тогда все решения уравнения имеют вид

где параметр t пробегает целые числа.

Доказательство. Пусть x, y – произвольное решение неопределенного уравнения. Тогда ax+by = c, где x, y Z. Вычтем из равенства ax+by = c равенство ax0 + by0 = c. Получим a(x − x0) + b(y − y0) = 0. Отсюда

Подставив x − x0 = bt в (11.23), имеем

abt = b(y0 − y), откуда at = y0 − y, и y = y0 − at.

Получили, что пара (x, y) имеет вид (11.22).

Обратно, пусть t Z. Подставив в левую часть уравнения (11.21) x = x0 + bt и y = y0 − at, имеем

a(x0 + bt) + b(y0 − at) = ax0 + by0 = c.

Поэтому пара (x, y) – решение уравнения. Теорема доказана.

57

Лекция 12. Системы сравнений первой степени.

Рассмотрим произвольную систему сравнений первой степени

Решением данной системы является число, которое удовлетворяет каждому сравнению этой системы. Если какое-то из сравнений в системе не имеет решения, то, очевидно, что система несовместна.

Решение системы (12.1) удобнее рассмотреть на примере. ПРИМЕР. Решить систему

По свойству сравнений в любом из сравнений коэффициенты можно заменить на сравнимые по соответствующему модулю. Получим равносильную, более простую систему

Рассмотрим первое сравнение 5x ≡ 1 (mod 7). Так как (5, 7) = 1, то сравнение имеет единственное решение. Найдем это решение подбором,

имеют вид x = 3 + 7t, где t – произвольное целое число.

Идея решения системы состоит в следующем. При любом целом t число x = 3 + 7t является решением первого сравнения. Подставим x во второе сравнение, и подберем те значения t, при которых верно также и второе сравнение. Получаем −3−7t ≡ −2 (mod 5), т. е. −7t ≡ 1 (mod 5)

и ≡ . Подбором находим решение ¯.

3t 1 (mod 5) 2

Поэтому t = 2 + 5t1, где t1 Z. Подставив t = 2 + 5t1 в равенство x = 3 + 7t, получим x = 17 + 35t1, где t1 – произвольное целое число.

Числа x = 17+35t1 при любом t1 Z удовлетворяют первому и второму сравнению. Подберем те значения t1, при котором верно также и третье

58

сравнение. Разделим вначале коэффициенты сравнения 2x ≡ 4 (mod 11) на число 2, взаимно простое с модулем m = 11. Получим x ≡ 2 (mod 11)

Подставив x = 17+35t1 в это сравнение, имеем 17+35t1 ≡ 2 (mod 11), т.е. 6 + 2t1 ≡ 2 (mod 11). Тогда 2t1 ≡ −4 (mod 11), t1 ≡ −2 (mod 11), t1 = −2 + 11t2 для t2 Z. Тогда x = 17 + 35t1 = 17 + 35(−2 + 11t2) =

=−53 + 385t2, где t2 Z. Отсюда x ≡ 332 (mod 385). Ответ. Решение системы имеет вид x ≡ 332 (mod 385).

Сравнения n-ой степени по простому модулю. Рассмотрим другой важный вид сравнений

где f(x) = a0xn + a1xn−1 + · · · + an – произвольный многочлен с целыми коэффициентами. Решение сравнений по составному модулю m сводится к решению сравнения по простому модулю. Поэтому изучим вначале случай, когда m = p – простое число. Итак, необходимо решить сравнение

Рассмотрим упрощающий прием для замены данного сравнения на равносильное сравнение степени не выше p − 1. Разделим f(x) на многочлен xp − x. Получим f(x) = (xp − x)q(x) + r(x), где q(x), r(x) Z[x] и r(x) = b0xp−1 + · · · + bp – остаток отделения. Подставив в (12.5), получим

По теореме Ферма xp ≡ x (mod p) для всех x Z. Тогда для любого целого числа x имеем xp −x ≡ 0 (mod p). Поэтому сравнение (12.6) равносильно сравнению r(x) ≡ 0 (mod p), т.е. следующему сравнению степени

не выше p − 1

b0xp−1 + · · · + bp ≡ 0 (mod p).

ПРИМЕР. Решить сравнение

26x14 − 12x11 + 22x7 + 3 ≡ 0 (mod 7).

Решение. Заменим коэффициенты многочлена на сравнимые числа из полной системы вычетов 0, 1, 2, 3, 4, 5, 6. Получим равносильное сравнение

59

Разделив многочлен из (12.7) на x7 − x, получим сравнение степени не выше 6. Однако понижение степени можно выполнить проще.

По теореме Ферма x7 ≡ x (mod 7). Возводя в квадрат, получим x14 ≡ x2 (mod 7). Заменим в (12.7) выражение x14 на сравнимое выражение x2. Далее x11 ≡ x5 (mod 7) и x7 ≡ x (mod 7). Поэтому заменим в сравнении (12.7) x11 на x5, а x7 на x. Вместо сравнения (12.7) рассмотрим равносильное сравнение

которое решим методом перебора всех возможных решений. Можно рассмотреть полную систему вычетов 0, 1, 2, 3, 4, 5, 6 по модулю 7 и проверим, какие из этих чисел удовлетворяют сравнению (12.8). Однако удобнее проверить числа из полной системы вычетов 0, 1, 2, 3, −3, −2, −1. В результате проверки получаем, что решением является только число −3. При этом −3 ≡ 4 (mod 7).

Ответ. Сравнение имеет единственное решение x ≡ 4 (mod 7).

ТЕОРЕМА 12.1 . Пусть f(x) = a0xn + a1xn−1 + · · · + an – многочлен с целыми коэффициентами. Предположим, что сравнение f(x) ≡ 0 (mod p), где p – простое число, имеет n + 1 решение. Тогда все коэффициенты многочлена f(x) делятся на p.

Доказательство. Обозначим через x0, x1, . . . , xn данные n + 1 решений. Поскольку решения различны, то

+d(x − xn−1)+ +e,

где целые коэффициенты a, b, c, d, . . . , e подберем двигаясь по (12.10) сверху вниз. Приравняем коэффициенты при xn в левой и правой частях в (12.10). Получим a = a0. Затем подбираем число b. Для этого вычислим

60