4. Интегрирование иррациональностей
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ:
Вычислить интеграл:
.
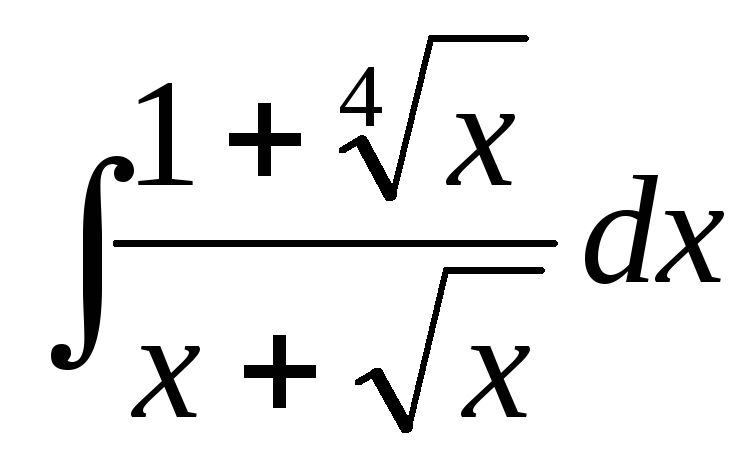РЕШЕНИЕ:
Подинтегральная
функция записана как функция от корней
степеней 2 и 4. Так как наименьшее общее
кратное степеней 2 и 4 равно 4, то данный
интеграл является интегралом типа
,
который рационализируется заменой:
.
Тогда
.
Имеем:
Получили интеграл от рациональной функции. Чтобы его вычислить, в числителе добавим и вычтем 1, после чего почленно разделим числитель на знаменатель, выделяя целую часть исходной дроби:
Первый
и третий интегралы табличные, а второй
берем заменой переменной:
.
Тогда
.
Получаем:
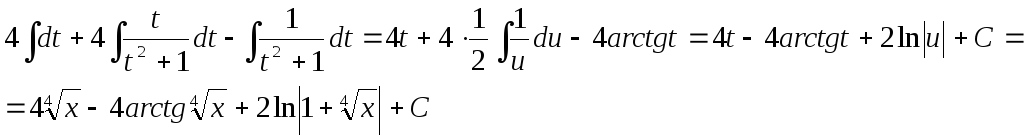
Вычислить интеграл:
.
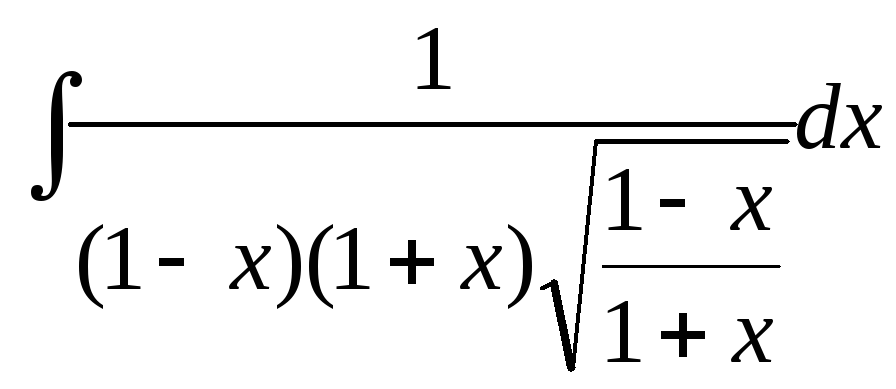РЕШЕНИЕ:
Имеем
интеграл вида
,
который вычисляется заменой
.
В нашем случае:
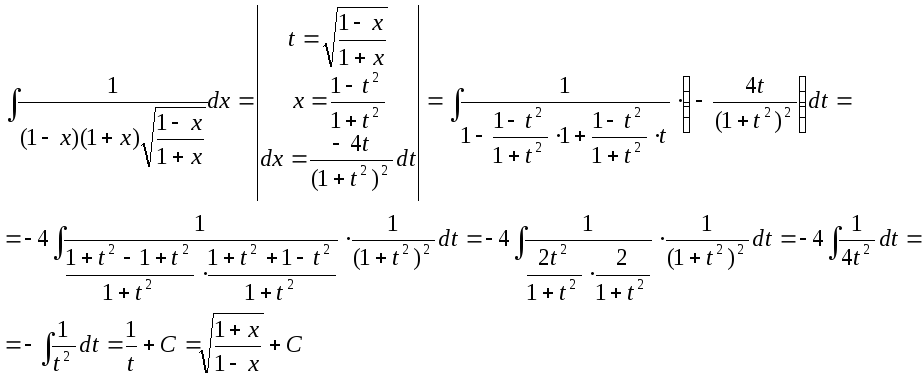
Вычислить интеграл:
.
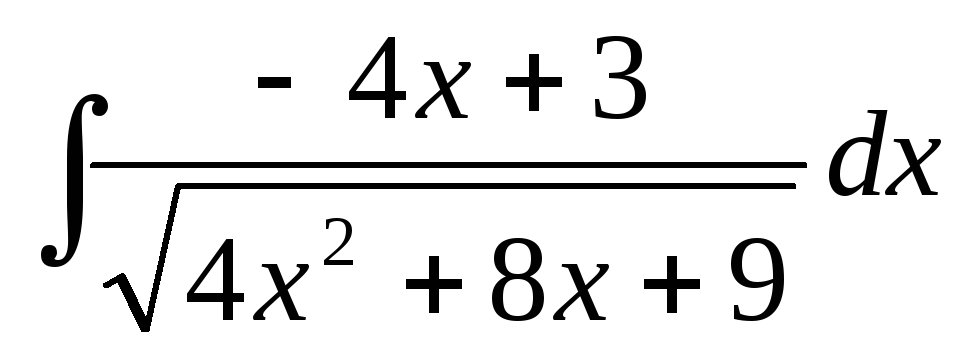РЕШЕНИЕ:
В
знаменателе дроби под корнем квадратный
трехчлен:
.
Выделяем полный квадрат:
.
Тогда
делаем замену
.
Следовательно,
и
.
Имеем:
.
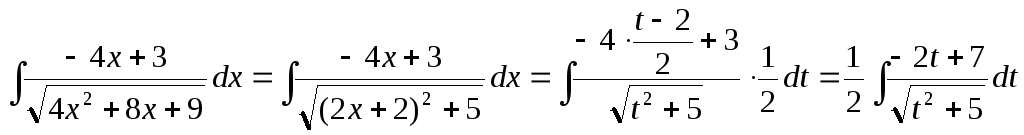Делим почленно числитель на знаменатель и представляем как сумму двух интегралов:
Первый
интеграл берем заменой
.
Тогда
.
Второй интеграл табличный.
Имеем:
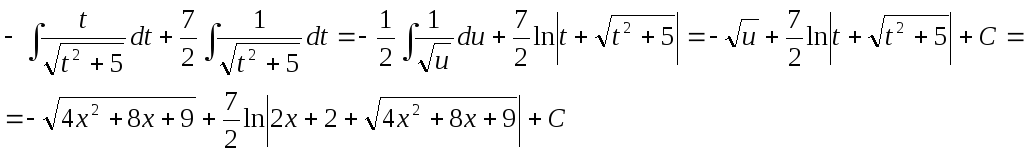
Заметим,
что данный интеграл можно также вычислить
методом выделения в числителе производной
знаменателя. Этот метод всегда удобно
использовать, когда в числителе стоит
линейная функция, а в знаменателе –
квадратный трехчлен. Производная
знаменателя в нашем случае будет равна
.
Запишем в числителе
,
тогда чтобы выражение в числителе
осталось прежним необходимо умножить
на
и прибавить 7. Несложно заметить, что
,
то есть выражение не изменилось. Тогда
имеем:
.
Поскольку
есть производная от знаменателя, тогда
будучи подведенным под знак дифференциала
это выражение даст значение знаменателя
и первый интеграл легко сводится к
табличному, второй интеграл берется
аналогично предыдущему решению, то есть
выделением полного квадрата . Окончательно
получим:
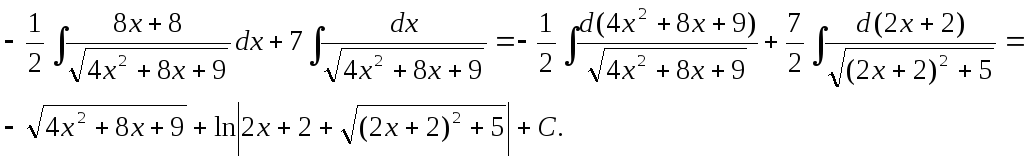
Вычислить интеграл:
.
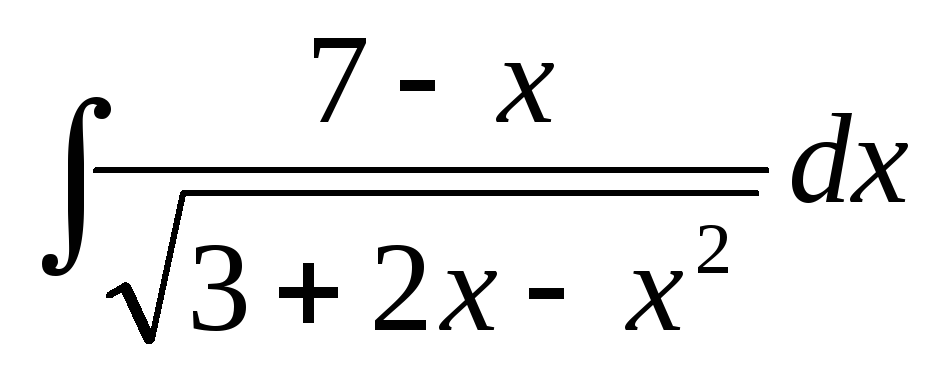РЕШЕНИЕ:
По аналогии с предыдущим случаем, выделяем полный квадрат под корнем и делаем соответствующую замену:
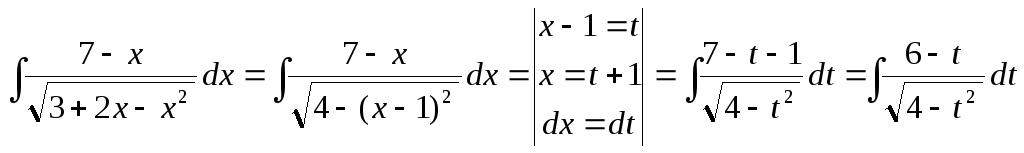
Представляем
этот интеграл как разность двух
интегралов. Первый будет интеграл
табличный. Второй снова берем заменой:
.
Тогда
.
Имеем:
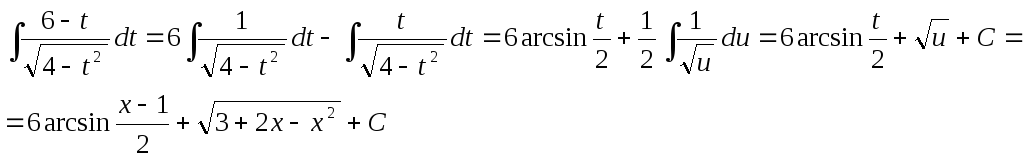
Решая тот же пример, методом выделения производной знаменателя имеем:
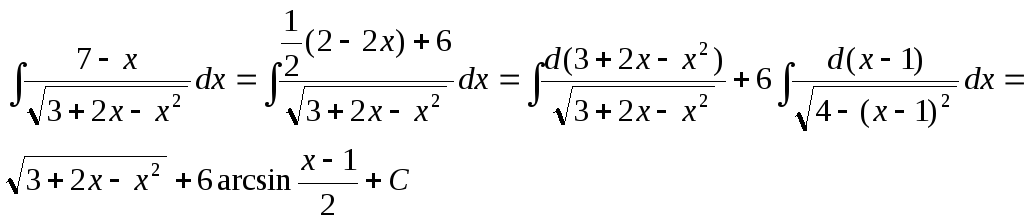
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:
Вычислить интегралы:
а)
б)
в)
г)
д)
е)
ж)
з)
и)
к)
л)
м)
н)
о)
п)
р)
с)
т)
у)
ф)
Интегрирование тригонометрических функций
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Вычислить интеграл:
.
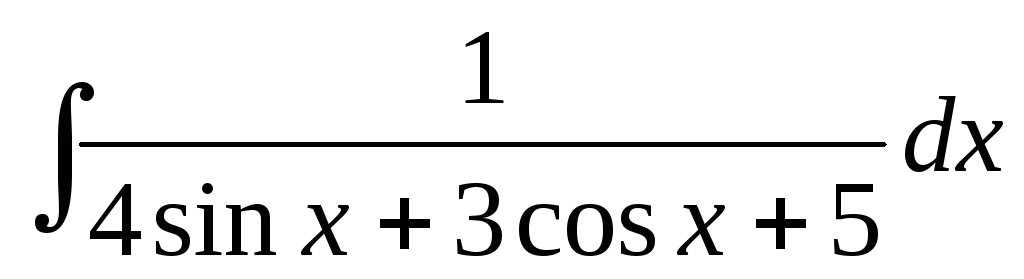РЕШЕНИЕ:
Используем
для вычисления этого интеграла
универсальную тригонометрическую
подстановку:
.
Тогда
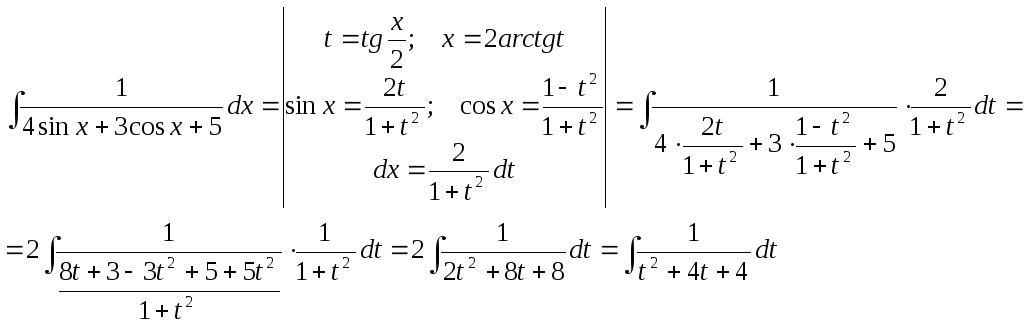
В полученном интеграле выделяем в знаменателе полный квадрат и делаем замену:
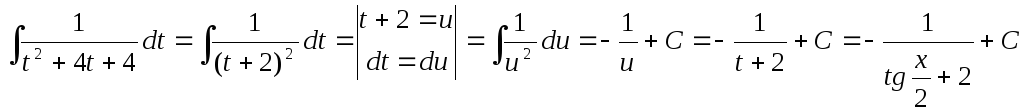
Вычислить интеграл:
.
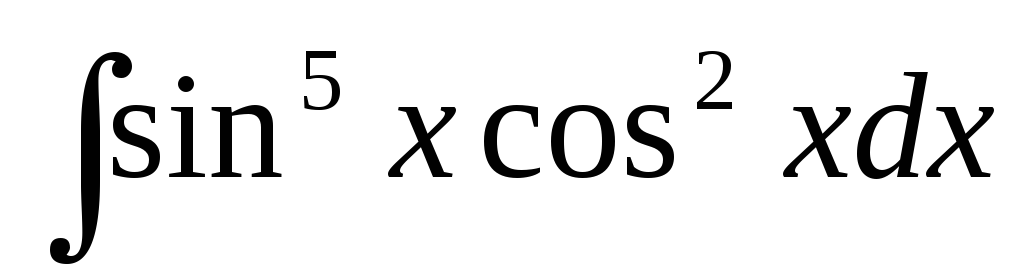РЕШЕНИЕ:
Данный
интеграл является интегралом вида
,
где
-
натуральные числа.
Если
-
четное,
-
нечетное, то используется подстановка
.
Если
-
четное,
-
нечетное, то используется подстановка
.
Если
-
нечетные, то используется любая из этих
подстановок.
Если
-
четные, то применяются формулы понижения
степени и интеграл сводится к одному
из трех рассмотренных выше типов.
В
нашем случае
.
Используем подстановку
.
Тогда
.
Поэтому один синус в подинтегральной
функции войдет под знак дифференциала.
Останется
.
Его заменяем с использованием основного
тригонометрического тождества:
.
Имеем:
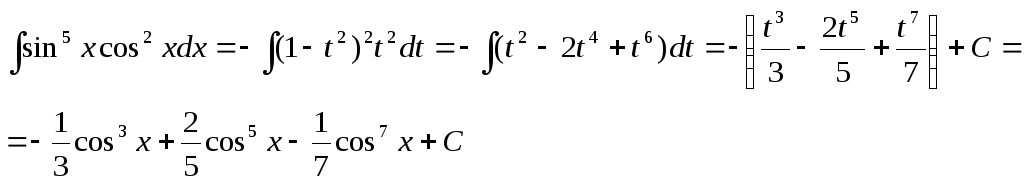
Вычислить интеграл:
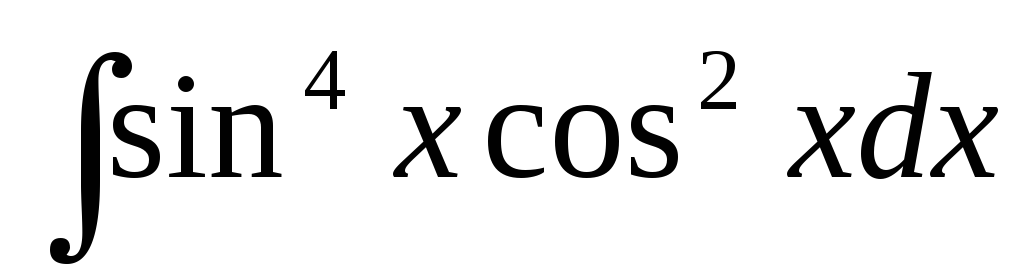
РЕШЕНИЕ:
Данный интеграл относится к рассмотренному выше типу интегралов. Поскольку степени у синуса и косинуса в подинтегральной функции четные, необходимо сначала использовать формулы понижения степени:
Имеем:
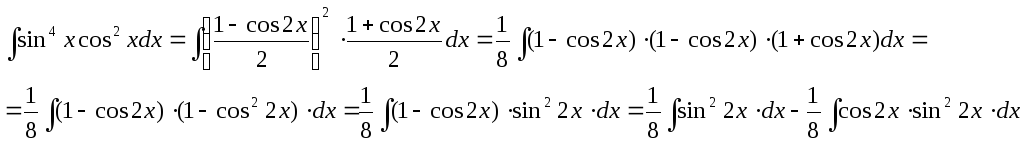
В
первом интеграле снова используем
формулу понижения степени, а во втором
подводим
под знак дифференциала либо делаем
замену:
.
Тогда
.
Получаем:
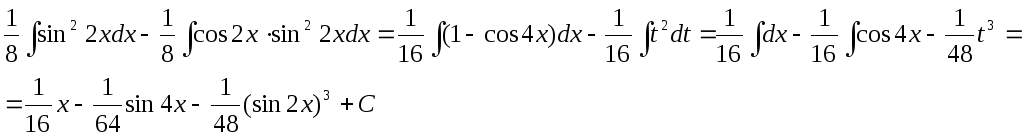
Вычислить интеграл:
.
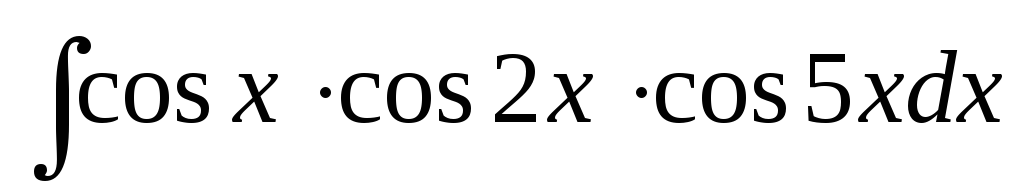РЕШЕНИЕ:
Данный
интеграл относится к интегралам вида
.
Для вычисления такого интеграла
произведение тригонометрических функций
преобразуется с помощью известных
формул в сумму. Таким же образом
вычисляются интегралы вида
и
.
В нашем случае используем формулу
.
Поскольку под знаком интеграла стоит произведение трех косинусов, то данную формулу применяем дважды.
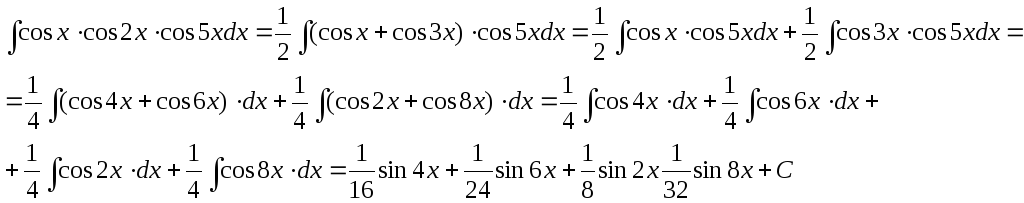
Вычислить интеграл:
.
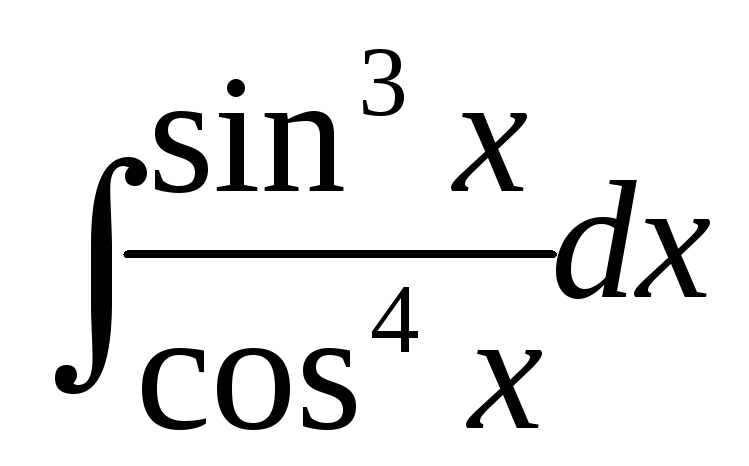РЕШЕНИЕ:
Используем
замену:
.
Тогда
и один из синусов в числителе войдет
под знак дифференциала новой переменной.
Останется
.
Получим:
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:
Вычислить интегралы:
а)
б)
в)
г)
д)
е)
ж)
з)
и)
к)
л)
м)
н)
о)
п)
р)
с)
т)
у)
ф)