Тема 1. Дифференциалы и элементарное интегрирование
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Найти приращение функции
,
и ее дифференциал.
РЕШЕНИЕ:
Сначала
находим приращение функции
по
формуле
,
где
-
приращение аргумента функции:
Теперь находим дифференциал функции, используя его определение:
Сравнивая
полученные выражения, видим, что, согласно
определению дифференциала функции, он
представляет собой главную, линейную
относительно
часть
приращения функции.
Найти дифференциал функции
.
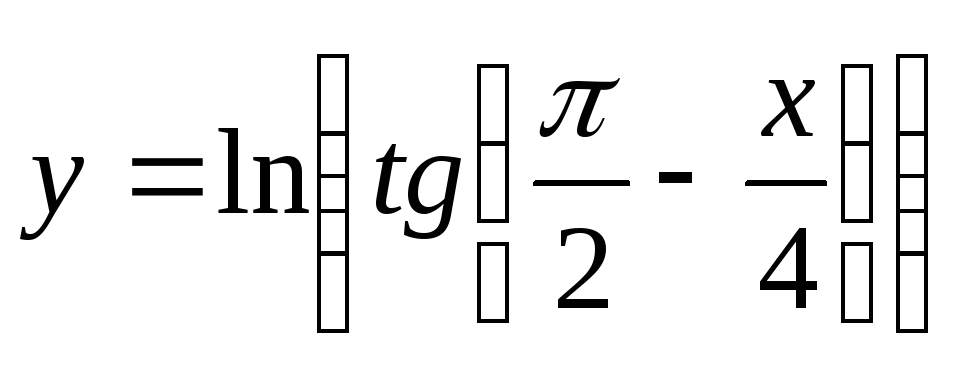РЕШЕНИЕ:
Снова используем определение дифференциала. При этом учитываем, что производная будет браться от сложной функции:
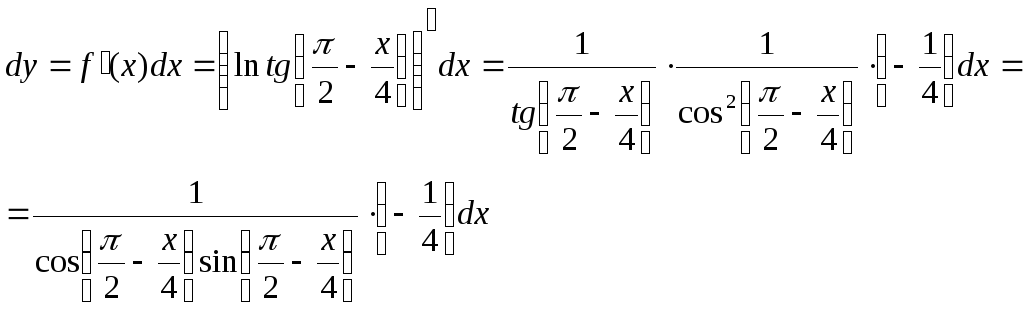
Найти формулу для приближенного вычисления
и найти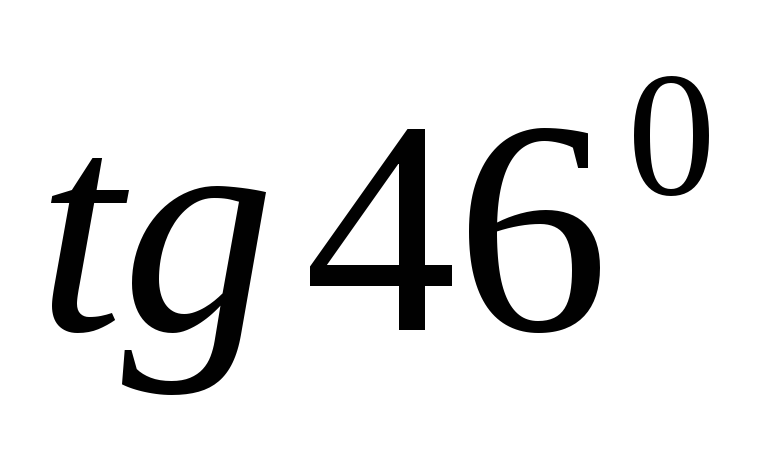
.
РЕШЕНИЕ:
Приращение функции приближенно можно считать равным сумме самой функции и ее дифференциала:
В
нашем случае
,
тогда
.
Следовательно,
Пользуясь
этой формулой, вычислим
.
можно
представить как
.
Следовательно,
.
Тогда
Вычислить интеграл
.
РЕШЕНИЕ:
Чтобы преобразовать данный интеграл к табличному, раскроем в числителе куб суммы и результат почленно разделим на знаменатель:
Интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих функций. Поэтому
Выносим постоянные множители за знаки интегралов:
Полученные
интегралы представляют собой интегралы
от степенной функции
.
Интеграл от степенной функции является
табличным и равен
если
,
и
,
если
.
Тогда
В конце решения записываем одну общую постоянную С, не выписывая постоянных от интегрирования отдельных слагаемых. В дальнейшем будем опускать постоянные от интегрирования отдельных слагаемых до тех пор, пока выражение содержит хотя бы один неопределенный интеграл. В окончательном ответе всегда будет одна постоянная.
Вычислить интеграл
.
РЕШЕНИЕ:
Преобразуем выражение, стоящее под знаком интеграла таким образом, чтобы свести его к табличному интегралу от показательной функции
.
Нам
нужно преобразовать подынтегральное
выражение таким образом, чтобы показатель
степени в выражении
совпадал с переменной под знаком
дифференциала. Для этого умножим
переменнуюх
под знаком
дифференциала на 3, тогда чтобы значение
интеграла не изменилось перед интегралом
нужно добавить коэффициент
.
Затем воспользуемся тем свойством, что
к переменной под знаком дифференциала
можно прибавлять любое число без
изменения его значения, поскольку
производная от любой константы есть
нуль. Получим
Вычислить интеграл
.
РЕШЕНИЕ:
Этот интеграл сводится к табличному интегралу вида:
Для
этого необходимо вынести множитель 4
из знаменателя, так чтобы коэффициент
при
оказался равен 1. Тогда за знак интеграла
выйдет численный множитель
:
Вычислить интеграл
.
РЕШЕНИЕ:
По аналогии с предыдущим примером, этот интеграл сводится к табличному интегралу вида
вынесением
множителя при
из под квадратного корня:
Вычислить интеграл:
.
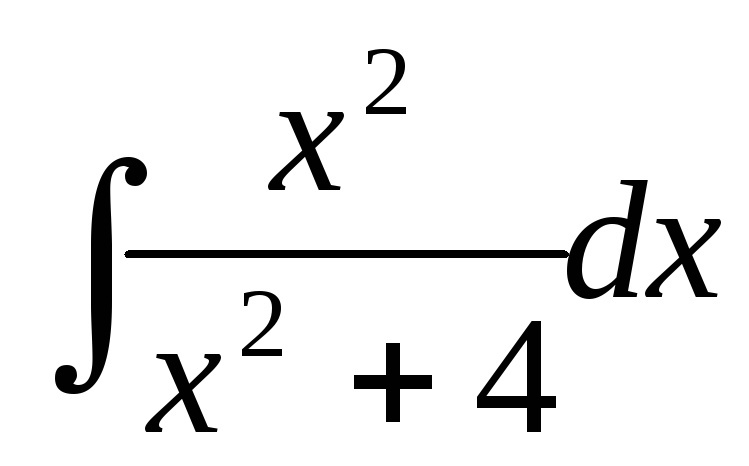РЕШЕНИЕ:
Чтобы вычислить этот интеграл, нужно выделить в подинтегральной функции целую часть. Для этого к выражению, стоящему в числителе, прибавляем и вычитаем 4 (выражение от этого не изменится):
Теперь почленно разделим числитель на знаменатель и представим полученный интеграл в виде разности двух интегралов, которые уже будут табличными:
Вычислить интеграл:
.
РЕШЕНИЕ:
В подинтегральном выражении раскроем квадрат суммы и воспользуемся тригонометрическими формулами:
Здесь мы учли, что
.
Теперь полученный интеграл разбиваем на сумму двух интегралов, которые являются табличными:
.
Вычислить интеграл:
.
РЕШЕНИЕ:
Раскроем скобки в подинтегральном выражении и разобьем интеграл на разность двух интегралов:
Первый интеграл табличный от показательной функции:
Второй
интеграл легко приводится к такому же
виду.
Для
этого умножим переменную под дифференциалом
на
,
тогда аналогичный множитель появится
перед знаком интеграла:
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Найти приращение функции и ее дифференциал:
а)
;
б)
;
в)
Найти дифференциалы функций:
а)
;
б)
;
в)
;
г)
1.3. Вычислить интегралы:
а)
б)
в)
г)
д)
е)
ж)
з)
и)
к)
л)
м)
н)
о)
п)
р)
с)
т)
у)
ф)
х)
ц)
ч)
ш)
щ)
э)