Занятие 3-4. Линейная зависимость системы векторов. Базисы. Координаты вектора в данном базисе

Цель занятия: Усвоить понятия линейно зависимой и линейно независимой системы векторов, понятия базиса векторного пространства и координат вектора.

Задачи

1. Система векторов является линейно независимой. Можно ли векторы,,

принять в качестве базиса в пространстве?

2. Векторы инеколлинеарны. Доказать, что система векторов,,является линейно зависимой. Найти координаты векторав базисе.

3. Точка – центр правильного шестиугольника. Найти координаты векторовв базисе.

4. В параллелепипеде точки– середины ребер. Найти координаты векторовв базисе,,.

5. Даны векторы . Определить координаты векторов:

а) ; б); в).

6. Можно ли выбрать в качестве базиса векторы:

а) ;

б) ?

Домашнее задание ИДЗ. Работа №1. Вектор и его координаты. [5].

Занятие 5-6.Скалярное умножение векторов

Цель занятия: Сформировать навыки применения скалярного умножения в решении геометрических задач.

Задачи

1. Даны векторы ,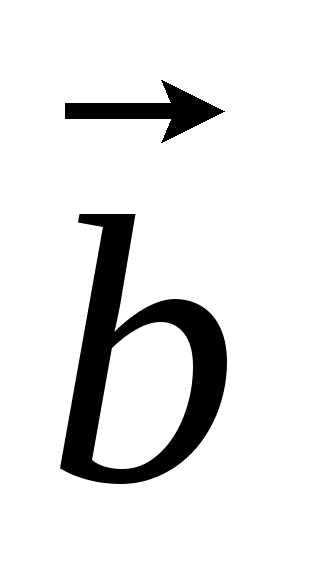и. Верны ли равенства: 1).;

2). ; 3).; 4).; 5).; 6).?

2. Найти длину вектора , если,.

3. Вычислить угол между диагоналями параллелограмма, построенного на векторах , где.

3. При каком значении векторыиортогональны, если,и?

4. Найти угол между векторами и, если векторыиортогональны.

5. В ортонормированном базисе ,. Доказать, что треугольникравнобедренный, вычислить его внутренние углы.

6. В ортонормированном базисе ,. Найти длину высотытреугольника.

7. Даны векторы ,и. Найти скалярную проекцию векторана направление вектора.

8. Вектор , длина которого равна, образует с базисными векторамиисоответственно углыи. Какой угол он образует с вектором?

9. Найти косинус угла при вершине равнобедренного треугольника, если медианы, проведенные из вершин основания, перпендикулярны между собой.

10.В кубе найти величину угла: а) между его диагональю и скрещивающейся с ней диагональю грани; б) между скрещивающимися диагоналями смежных граней; в) между диагональю куба и пересекающейся с ней диагональю грани.

Домашнее задание ИДЗ. Работа №2. Скалярное умножение векторов. [1].

Занятие 7. Векторное умножение векторов

Цель занятия: Сформировать навыки применения векторного умножения к решению задач.

Задачи

1. Вычислить , если.

2. Векторы иортогональны и. Вычислить 1).; 2)..

3. Вычислить площадь параллелограмма, построенного на векторах ,, где,,.

4. В ортонормированном базисе . Вычислить.

5. Найти площадь треугольника , если в ортонормированном базисе.

6. В ортонормированном базисе ,. Найти высотутреугольника.

Домашнее задание

1. Найти площадь треугольника , если.

2. Найти синус угла между векторами и, если.

Занятие 8. Смешанное умножение векторов

Цель занятия: Сформировать навыки применения смешанного умножения к решению геометрических задач.

Задачи

1. В ортонормированном базисе ,. Определить ориентацию этой тройки векторов.

2. В некотором базисе . Выяснить, компланарны ли эти векторы.

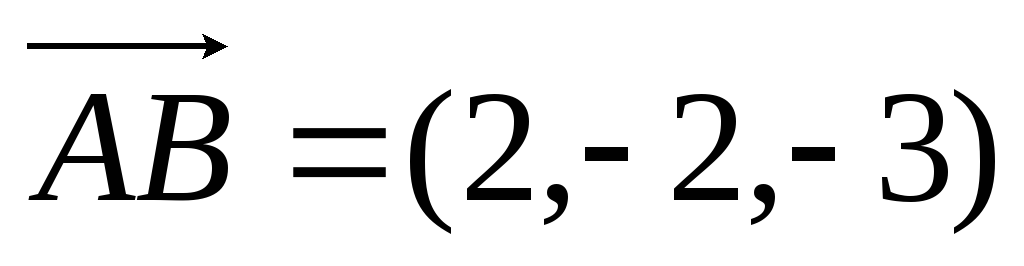3. В ортонормированном базисе ,. Найти высоту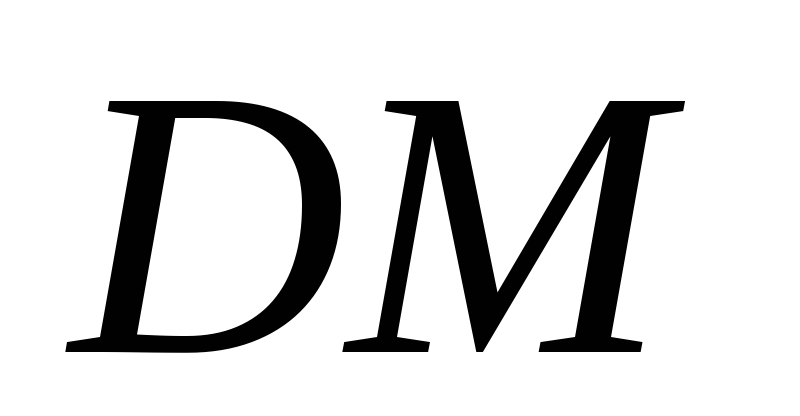тетраэдра.

4. Объем параллелепипеда равен 5. В ортонормированном базисе. Найти координаты вектора, если он ортогонален векторами.

5. Точки – центры тяжести граней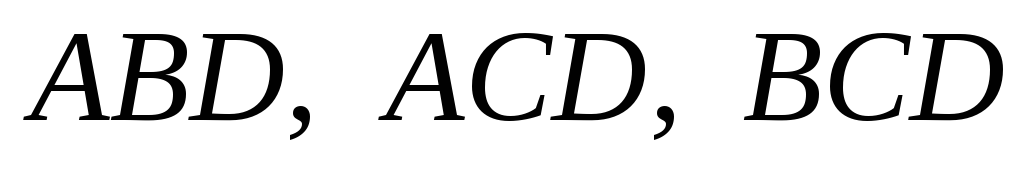тетраэдра. Найти отношение объемов тетраэдрови.

Домашнее задание ИДЗ. Работа № 3. Векторное и смешанное умножение векторов. [5].