Занятие 15. Параллельный перенос и поворот плоскости

Задачи

1. При переносе на вектор 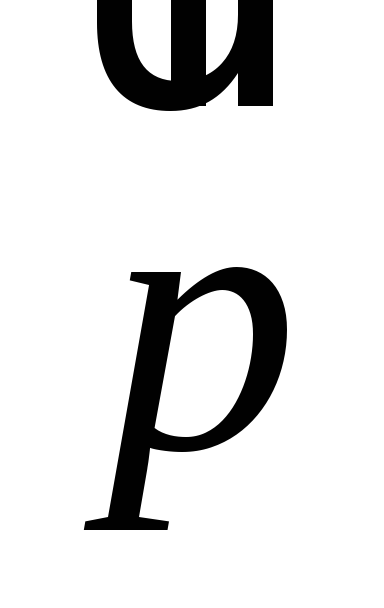точкапереходит в точку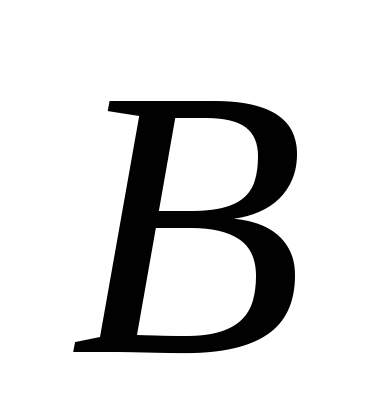, а при переносе на векторточка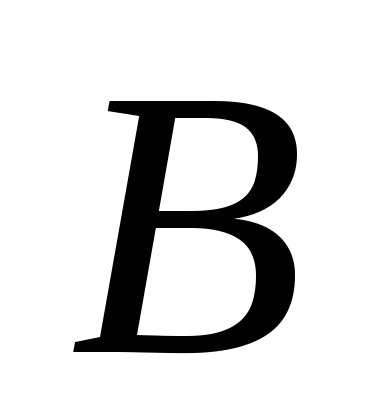переходит в точку. Найти: а) образ точкипри переносе на вектор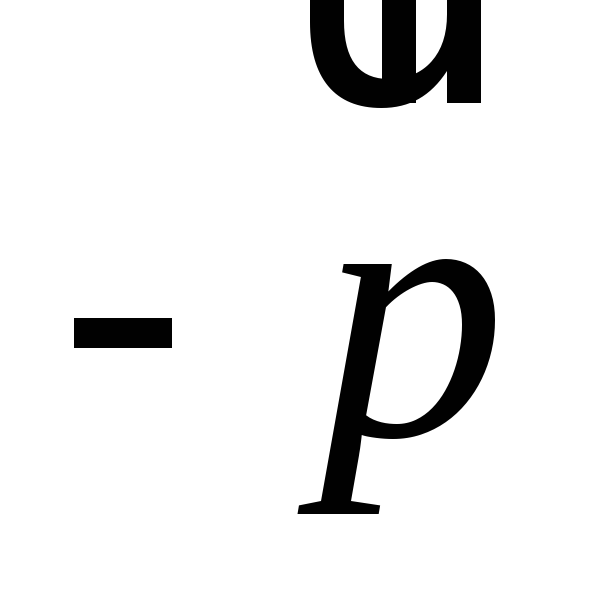; б) образ точкипри переносе на вектор.

2. Длины отрезков иравны. Отображениеплоскости переводит данную точкув точкуи точкув точку. Является ли отображениепараллельным переносом?

3. Сколько существует параллельных переносов плоскости, отображающих прямую на параллельную ей прямую?

4. Доказать, что параллельный перенос является преобразованием плоскости.

5. Составить формулы параллельного переноса на вектор 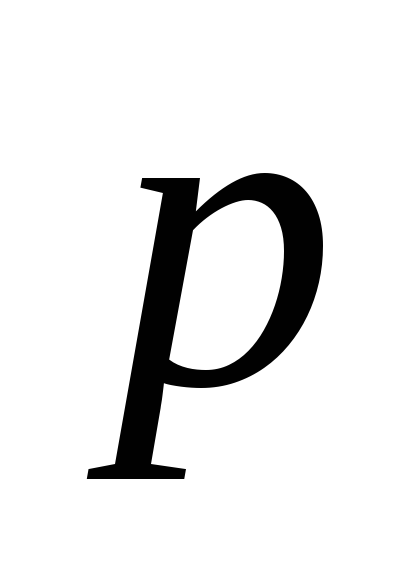, если известно, что при этом переносе точкаA (1; 2) переходит в точку А₁, принадлежащую прямой и.

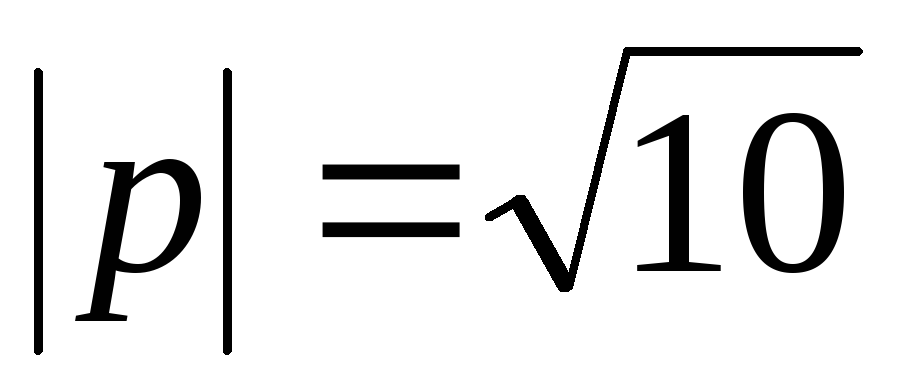6. Относительно группы параллельных переносов являются эквивалентными следующие фигуры:

1) две окружности одного и того же радиуса; 2) два направленных отрезка одинаковой длины и одного направления; 3) сонаправленные лучи; 4) два квадрата с равными сторонами?

7. Дан параллелограмм 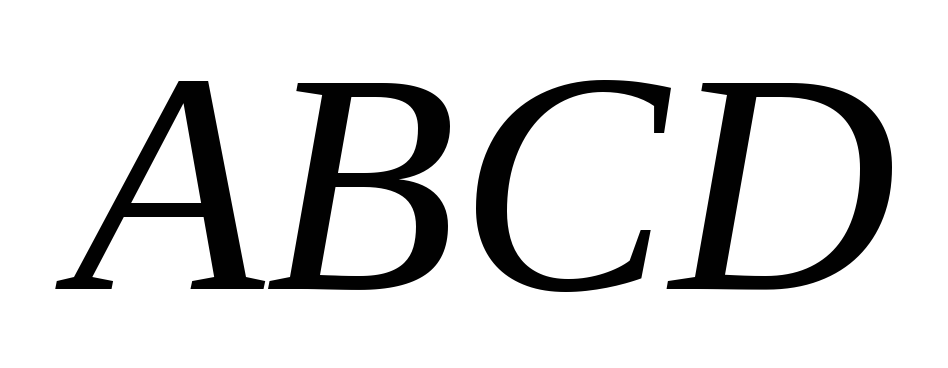;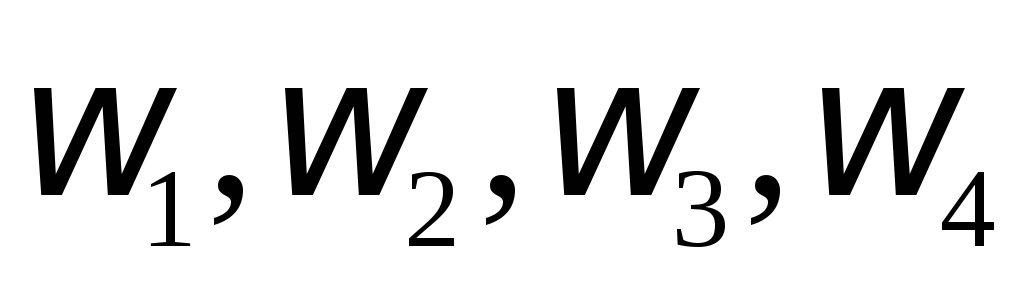– окружности радиуса R с центрами в точкахсоответственно. Найти:

1) образы окружностей ипри переносе на вектор;

2) образы окружностей ипри переносе на вектор;

3) образ прямой, проходящей через точку и перпендикулярной прямой, при переносе на вектор.

8. Дан правильный треугольник (буквы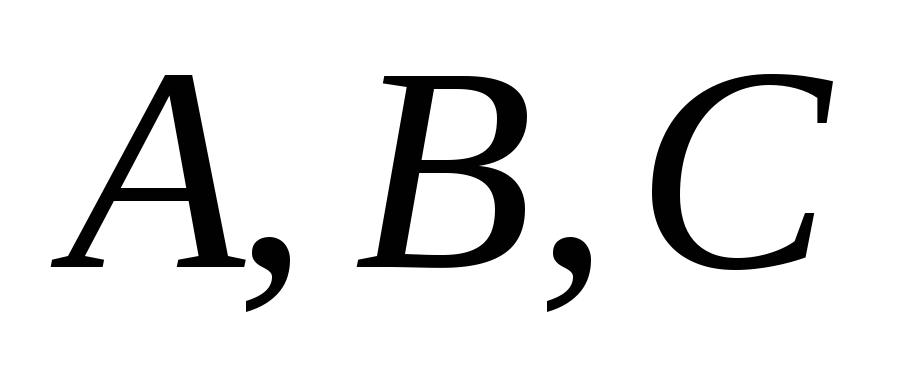расставлены в порядке обхода вершин по часовой стрелке); точка– центр треугольника. Укажите: а) образ точкипри повороте;

б) образ точки B при повороте ;

в) образы точек A, B, C при повороте ;

г) образы точек A, B, C при повороте .

9. Сколько существует различных поворотов, переводящих точку в точку?

10. Дан квадрат ABCD с центром O. Найти образы следующих фигур при повороте :

1. луч AB;

2. прямая, проходящая через точку B и параллельная прямой AC;

3. полуплоскость, определяемая прямой BC и содержащая точку O.

11. Дан правильный треугольник ABC с центром O. Найти образы следующих фигур при повороте :

1. отрезок BC;

2. луч CA;

3. полуплоскость, определяемая прямой AB и не содержащая точку O.

12. При повороте точкапереходит в точку. Составить формулы поворота, если известно, что его центр принадлежит прямой. Найти образ начала координат при этом повороте.

13. При центральной симметрии Z_А точка М переходит в точку K, а при центральной симметрии Z_В точка K переходит в точку P. Доказать, что при переносе на вектор точкаM переходит в точку P.

14. Доказать, что всякое преобразование плоскости, заданное в аффинном репере формулами ,, является центральной симметрией с центром в точкеS (x₀; y₀).

15. На прямой найти точку, которая при центральной симметрии с центром в начале координат переходит в точку, принадлежащую прямой.

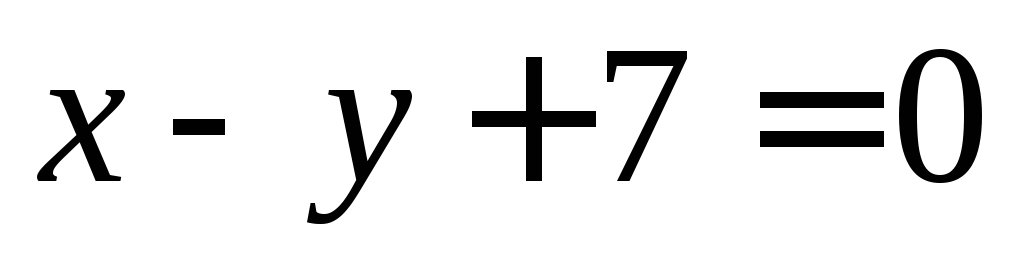16. Составить формулы центральной симметрии Z_S, при которой точка переходит в точку, принадлежащую прямой, если известно, что центрS принадлежит прямой x+y–5=0.

17. Относительно группы поворотов с общим центром следующие фигуры являются эквивалентными:

1) две гиперболы с центром в точке ; 2) два луча с началом в точке; 3) две произвольные прямые; 4) две прямые, одинаково удаленные от точки?